
08-09高数(上)期中试题 一、填空3分×27=81分) 1.设f(x)的定义域D=[0,1],f(x-a),(a>0)的 定义域D,=[a,a+1] 0≤x-a≤1, a≤x≤a+1, 2.1g(0+3x)= m(1+3x)=lim+3x)3=e
08-09高数(上)期中试题 1 2 f x D = f x - a a [0,1], ( ),( 0) D = 1.设 ( )的定义域 的 定义域 ( ) 1 0 lim 1 3 x x x → 2. + = 一 、填空(3 27 81 分 = 分) 0 1, − x a a x a+ 1, [ 1] a,a+ ( ) ( ) 1 1 3 3 3 0 0 lim 1 3 lim 1 3 x x x x x x e → → + = + =
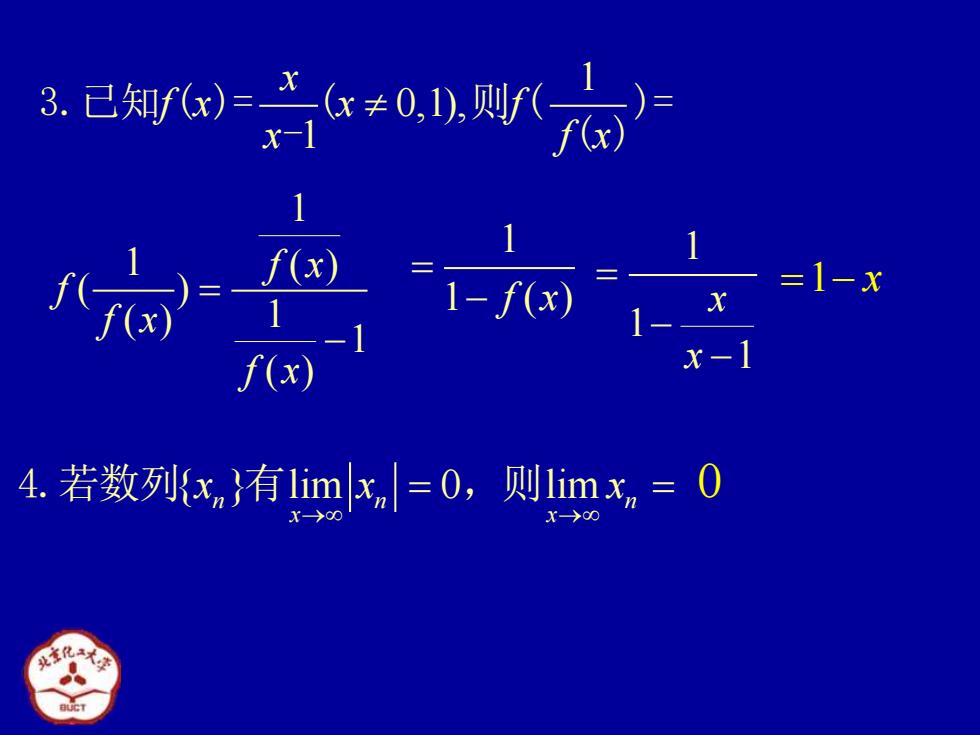
3已w六=7友 f(x) 4.若数列{xn}有1imx=0,则1imxn=0 r-so →00
1 0,1), 1 x f x x f x f x 3.已知 ( )= ( 则 ( )= - ( ) 1 1 ( ) ( ) ( ) 1 1 ( ) f x f f x f x = − 1 1 ( ) f x = − = −1 x 1 1 1 x x = − − { } lim 0 lim n n n x x x x x → → 4.若数列 有 = = ,则 0

5.lim x→+arccotx In lim lim x→+arccotx x→+arc cot x 1 lim 1+x2 =lim x>+∞ x-+o0 =1 1+x2
1 ln 1 5 lim cot x x →+ arc x + . = =1 1 lim cot x x →+ arc x 2 2 1 lim 1 1 x x x →+ − = − + 2 2 1 lim x x →+ x + = 1 ln 1 lim cot x x →+ arc x + =
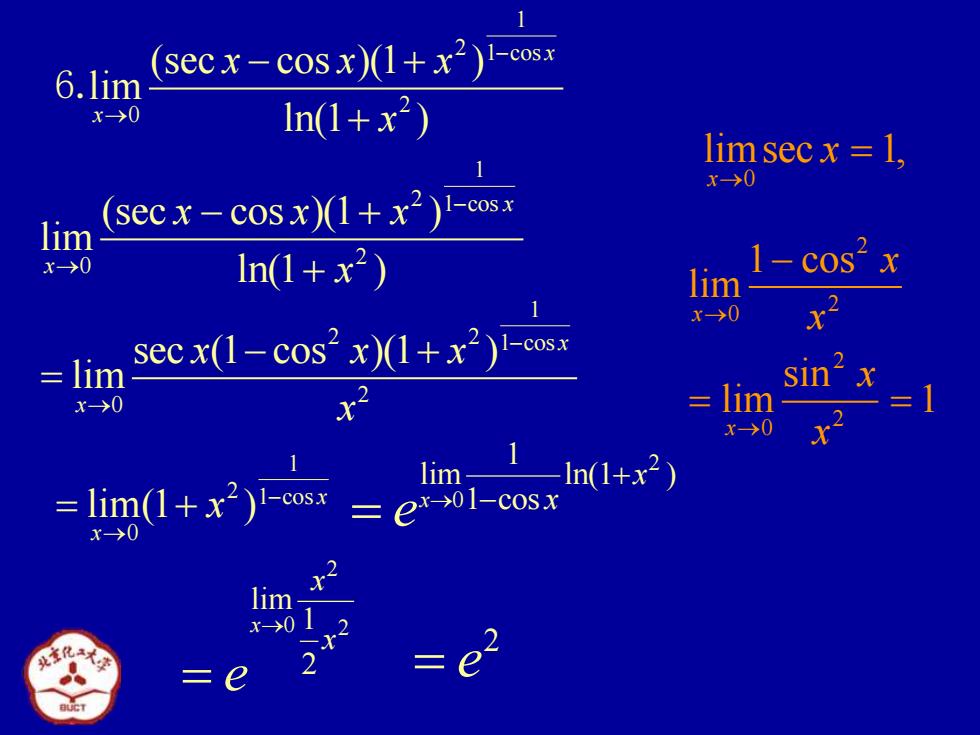
6.lim (secx-cosx)(1+x2)1-cosx x→0 In(1+x2) limsecx =1, x-)0 lim (secx-cosx)(1+x2)1-cosx x-→0 ln(1+x2) lim 1-cosx lim Seex(1-cos'(1+ x→0 x sin2 x x→0 lim =1 =lim1+x2))-eosx lim,In(+x2) =e1w x0 2 lim x-0 =e
1 2 1 cos 2 0 (sec cos )(1 ) lim ln(1 ) x x x x x x − → − + + 6. 2 = e 1 2 2 1 cos 2 0 sec (1 cos )(1 ) lim x x x x x x − → − + = 1 2 1 cos 0 lim(1 ) x x x − → = + 2 0 1 lim ln(1 ) x 1 cos x x e → + − = 2 0 2 lim 1 2 x x x e → = 1 2 1 cos 2 0 (sec cos )(1 ) lim ln(1 ) x x x x x x − → − + + 0 limsec 1, x x → = 2 2 0 2 2 0 1 cos lim sin lim 1 x x x x x x → → − = =

7.若数列x,}满足对Vn,xn>0且lim=a,则a的取值范围 a≥0 8.给间断点分类:点x= 是函数y=X的 间断点 tan x lim* 第一类可去间断点 x→tanx 9.无穷小阶的比较:当x→>0时,f(x)=2+3-2与x 比较是同阶 无穷小 lim 2*+3-2 2-1 +3- x→0 x→0 X xIn 2 lim lim xIn3 =1n2+ln3=1n6 x)0 x→0X
2 tan x x y x 8.给间断点分类:点 = = 是函数 的 间断点 2 lim 0 x tan x x → = { } , 0 lim , n n n n x n x x a a → 7.若数列 满足对 = 且 则 的取值范围 a 0 第一类可去间断点 9 0 ( ) 2 3 2 x x .无穷小阶的比较:当x f x x → = + − 时, 与 比较是 同阶 无穷小 0 0 2 3 2 2 1 3 1 lim lim( ) x x x x x x → → x x x + − − − = + = + = ln 2 ln3 ln6 0 0 ln 2 ln 3 lim lim x x x x → → x x = +