
Another Way a11 a12 a13 a11 412 D= a21 22 a23 a21 a22 a31 a32 a33 a31 a32 + Tongji University】 6/32
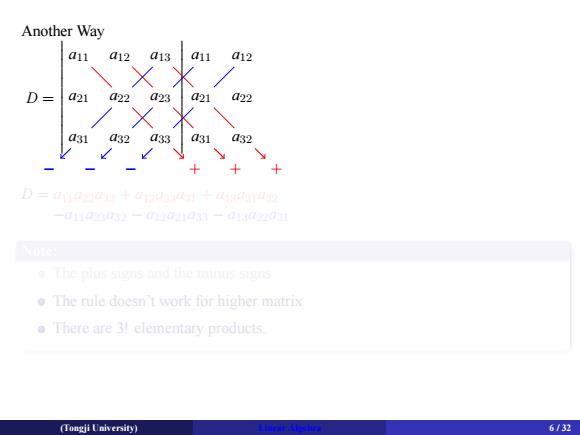
. Another Way D = . a11. a12. a13. a11. a12. a21. a22. a23. a21. a22. a31. a32. a33. a31. a32. . . . − − − + + + D = a11a22a33 + a12a23a31 + a13a21a32 −a11a23a32 − a12a21a33 − a13a22a31 . Note: . . The plus signs and the minus signs The rule doesn’t work for higher matrix There are 3! elementary products. (Tongji University) Linear Algebra 6 / 32

Another Way a11 Q12 a13 a11 412 D= a21 d22 a23 a21 a22 a31a32a33 a31 a32 + + D=0+出4十a2 一一一 Tongji University】 6/32
. Another Way D = . a11. a12. a13. a11. a12. a21. a22. a23. a21. a22. a31. a32. a33. a31. a32. . . . − − − + + + D = a11a22a33 + a12a23a31 + a13a21a32 −a11a23a32 − a12a21a33 − a13a22a31 . Note: . . The plus signs and the minus signs The rule doesn’t work for higher matrix There are 3! elementary products. (Tongji University) Linear Algebra 6 / 32
Another Way a11 a12 a13 a11 412 D=a21 122 a23 21 a22 a3132a33 a31 a32 + + + D=0十十a0 一112一203一21 The nit sions and the minus sans o The rule doesn't work for higher matrix There are 3!elementary products (Tongji University) 6/32
. Another Way D = . a11. a12. a13. a11. a12. a21. a22. a23. a21. a22. a31. a32. a33. a31. a32. . . . − − − + + + D = a11a22a33 + a12a23a31 + a13a21a32 −a11a23a32 − a12a21a33 − a13a22a31 . Note: . . The plus signs and the minus signs The rule doesn’t work for higher matrix There are 3! elementary products. (Tongji University) Linear Algebra 6 / 32

Another Way a11 Q12 a13 a11 412 D= a21 22 a23 21 a22 a31a32a33 31 a32 + D=a11a22a33+a12a23a31+a13a21a32 一112一043一21 Note: o The plus signs and the minus signs o The rule doesn't work for higher matrix There are 3!elementary products (Tongji University) 6/32
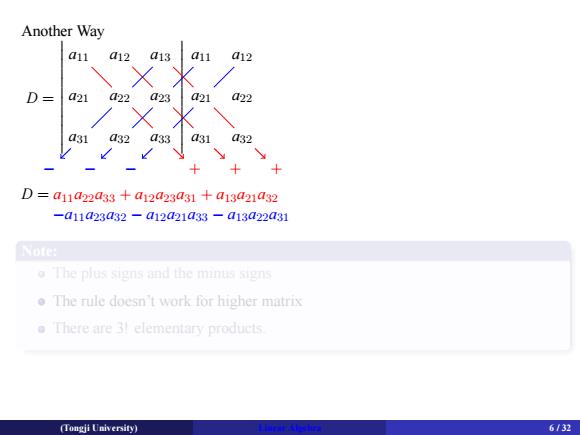
. Another Way D = . a11. a12. a13. a11. a12. a21. a22. a23. a21. a22. a31. a32. a33. a31. a32. . . . − − − + + + D = a11a22a33 + a12a23a31 + a13a21a32 −a11a23a32 − a12a21a33 − a13a22a31 . Note: . . The plus signs and the minus signs The rule doesn’t work for higher matrix There are 3! elementary products. (Tongji University) Linear Algebra 6 / 32
Another Way a11 Q12 a13 a11 412 D= a21 22 a23 21 a22 a31a32a33 a31a32 y + + D=a11a22a33+a12a23a31+a13a21a32 -a11a23a32-a12a21a33-a13a22a31 Note: o The plus signs and the minus signs o The rule doesn't work for higher matrix There are 3!elementary products (Tongji University) 6/32
. Another Way D = . a11. a12. a13. a11. a12. a21. a22. a23. a21. a22. a31. a32. a33. a31. a32. . . . − − − + + + D = a11a22a33 + a12a23a31 + a13a21a32 −a11a23a32 − a12a21a33 − a13a22a31 . Note: . . The plus signs and the minus signs The rule doesn’t work for higher matrix There are 3! elementary products. (Tongji University) Linear Algebra 6 / 32