本章内容 第6章图与网络优化 6.1图的基本概念 6.2最小支罐树 Graph Theory and 6.3最短路问思 Network Optimization 6.4网络最大流问题 2019-6-3 A A 1736年胶拉将这个间愿抽家 哥尼斯堡七桥问题 婚不出这个面形,聚 终回到原成。 不可在的文中了这是 顶点都与奇数条 相连接 的下名问 碳:豆族责能公失染典备发智七 一笔画问题 A性 △性 6.1图的基本橛念 球队比赛 一结指中的写之间的关联关系 e >端点 >关联点(相邻点) e >关联边(相邻边) A整 A性 1
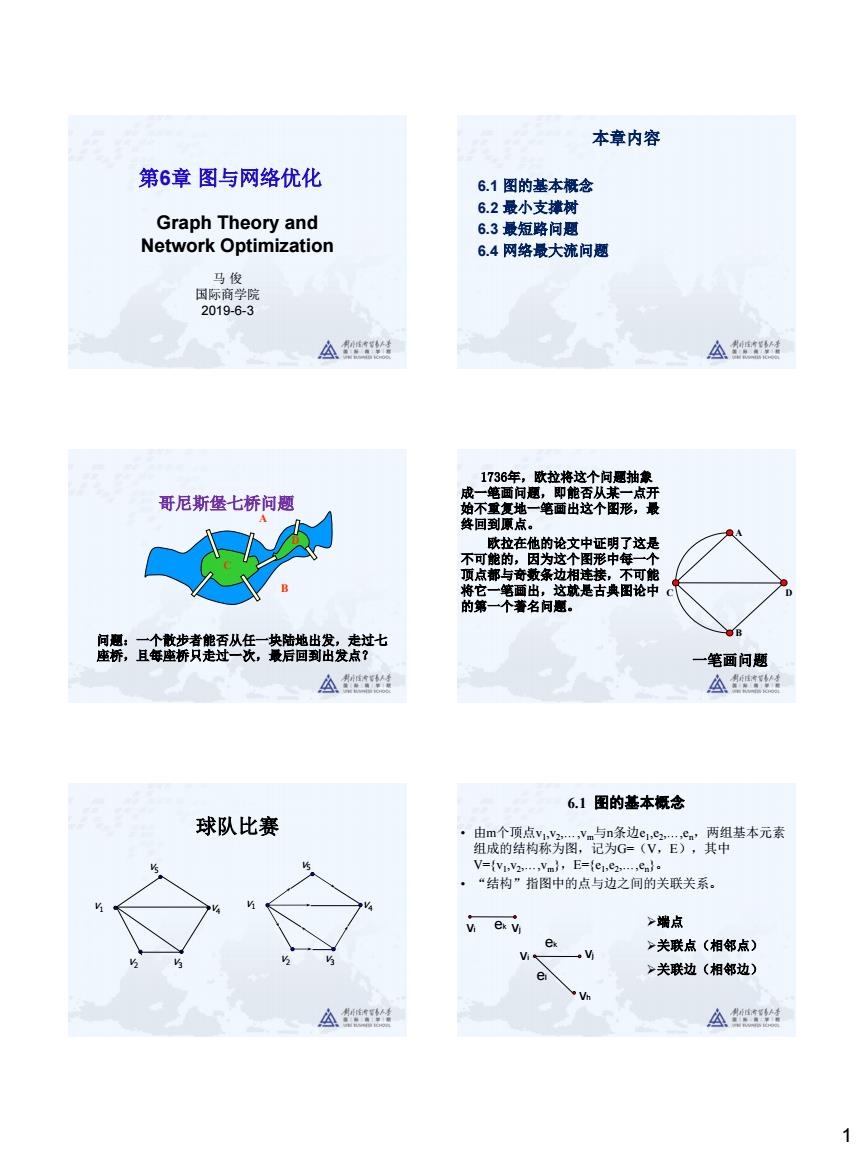
1 Graph Theory and Network Optimization 第6章 图与网络优化 马 俊 国际商学院 2019-6-3 6.1 图的基本概念 6.2 最小支撑树 6.3 最短路问题 6.4 网络最大流问题 本章内容 B A C D 哥尼斯堡七桥问题 问题:一个散步者能否从任一块陆地出发,走过七 座桥,且每座桥只走过一次,最后回到出发点? 1736年,欧拉将这个问题抽象 成一笔画问题,即能否从某一点开 始不重复地一笔画出这个图形,最 终回到原点。 欧拉在他的论文中证明了这是 不可能的,因为这个图形中每一个 顶点都与奇数条边相连接,不可能 将它一笔画出,这就是古典图论中 的第一个著名问题。 A B C D 一笔画问题 球队比赛 v1 v2 v3 v4 v5 v1 v2 v3 v5 v4 6.1 图的基本概念 • 由m个顶点v1 ,v2 ,…,vm与n条边e1 ,e2 ,…,en,两组基本元素 组成的结构称为图,记为G=(V,E),其中 V={v1 ,v2 ,…,vm},E={e1 ,e2 ,…,en}。 • “结构”指图中的点与边之间的关联关系。 vi e vj k vi vj ek el vh ➢端点 ➢关联点(相邻点) ➢关联边(相邻边)
6.1图的基本橛念 的 之间 带箭头的 叫做 如果 个图是由点和边所构 表示图 区公国 △ △ 无向图例子 有向图的例子 下图是一个无向图G=(W,) 其中y={,gvd E=vl,[vl,[小, [vs.V4],[VV,[vaVa.[va.Va -))(v.(V(V) (VgV ).(vsVj).(vsVD.(vsVo).(VoV) 其中v示有 记作,向的氧 图的分类 周无内图,记作G=心,目 有向图的边 图G或有向图D中的点数,记作pG)或D,简 有向图,记作D=(N, 称为。 例1:香尼斯桥问圆的图为 个无向图, 如果图G中,一条边的两个端点是相同的,事么称 例2:五个球队的比赛情况,V1→V2表示v1胜2 这条边是环,如图中的边[y,Y]是环。 如果两个点之间有两条以上的边,那么称它们为 多量边,如图中的边[v1,[v2】。 一个无环,无多量边的图称为葡单图 一个无环,有多置边的图称为多量图
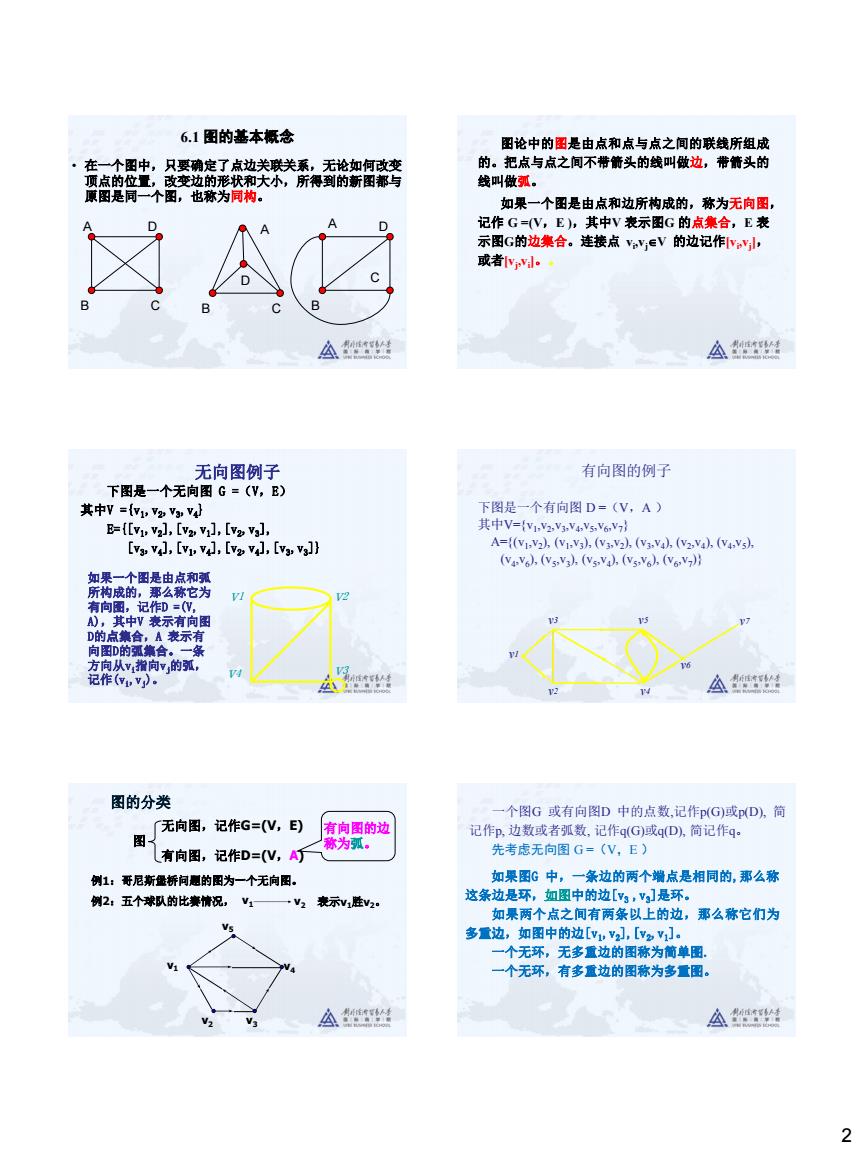
2 6.1 图的基本概念 • 在一个图中,只要确定了点边关联关系,无论如何改变 顶点的位置,改变边的形状和大小,所得到的新图都与 原图是同一个图,也称为同构。 A B C D A B C D A B C D 图论中的图是由点和点与点之间的联线所组成 的。把点与点之间不带箭头的线叫做边,带箭头的 线叫做弧。 如果一个图是由点和边所构成的,称为无向图, 记作 G =(V,E ),其中V 表示图G 的点集合,E 表 示图G的边集合。连接点 vi ,vjV 的边记作[vi ,vj ], 或者[vj ,vi ]。。 无向图例子 下图是一个无向图 G =(V,E) 其中V ={v1,v2,v3,v4} E={[v1,v2],[v2,v1],[v2,v3], [v3,v4],[v1,v4],[v2,v4],[v3,v3]} v3 v1 v2 v4 如果一个图是由点和弧 所构成的,那么称它为 有向图,记作D =(V, A),其中V 表示有向图 D的点集合,A 表示有 向图D的弧集合。一条 方向从vi指向vj的弧, 记作(vi,vj)。 有向图的例子 下图是一个有向图 D =(V,A ) 其中V={v1 ,v2 ,v3 ,v4 ,v5 ,v6 ,v7} A={(v1 ,v2 ), (v1 ,v3 ), (v3 ,v2 ), (v3 ,v4 ), (v2 ,v4 ), (v4 ,v5 ), (v4 ,v6 ), (v5 ,v3 ), (v5 ,v4 ), (v5 ,v6 ), (v6 ,v7 )} v3 v5 v7 v2 v4 v1 v6 图 无向图,记作G=(V,E) 有向图,记作D=(V,A) 例1:哥尼斯堡桥问题的图为一个无向图。 有向图的边 称为弧。 例2:五个球队的比赛情况, v1 v2 表示v1胜v2。 v1 v2 v3 v4 v5 图的分类 一个图G 或有向图D 中的点数,记作p(G)或p(D), 简 记作p, 边数或者弧数, 记作q(G)或q(D), 简记作q。 先考虑无向图 G =(V,E ) 如果图G 中,一条边的两个端点是相同的,那么称 这条边是环,如图中的边[v3 ,v3]是环。 如果两个点之间有两条以上的边,那么称它们为 多重边,如图中的边[v1,v2],[v2,v1]。 一个无环,无多重边的图称为简单图. 一个无环,有多重边的图称为多重图

链、简单链、韧等链、连通图 以点v为端点的边的个数称为点v的次,记作(W), 链:由两两相第的点及其相关联的边构成的点边序列 次为零的点称为氧立点: 如vg,01,1,2, 次为1的点称为悬挂点: 悬挂点的边称为悬挂边 分别为的惠点 次为奇戴的点称为奇点 前单 次为偶数的点称为俱点。 含的点均不相同 初等、前单 葡单圆:面中所含的边均不相同 A A 连通图:图中任意两点之间均至少 能测作不 有向图相关概念 基遍图:有向图中去掉所有或上的箭头, 很到的于向型 弧:有向图的边a=a,),惠点u,终点Y ,B2sB1,称G2是G的 路:若有从口到v不考虑方向的链,且 各方向一致,则称之为从u到v的略: 初等路:各顶点都不相同的略: 初等回路:u=v的初等略: A △世 无向图中的概念总结 无向图的性质 ,多量边 奇点 ·简单图 偶点 ·多重图 ·环 以下各点能不能是某简单图的项点的次的序列? 初等(单) 悬挂点 初等(简单)圆 悬挂边 连通图 ,孤立点 支撑子图 A性 A丝
3 以点v为端点的边的个数称为点v的次,记作d(v) 。 次为零的点称为弧立点; 次为1的点称为悬挂点; 悬挂点的边称为悬挂边; 次为奇数的点称为奇点; 次为偶数的点称为偶点。 链、简单链、初等链、连通图 链:由两两相邻的点及其相关联的边构成的点边序列; 如v0 ,e1 ,v1 ,e2 , v2 ,e3 ,v3 ,…,vn-1,en , vn ; v0 , vn分别为链的起点和终点 简单链:链中所含的边均不相同 初等链:链中所含的点均不相同 圈、初等圈、简单圈、 圈:v0 = vn 的链称为圈或闭链 初等圈:圈中所含的点均不相同 简单圈:圈中所含的边均不相同 连通图:图中任意两点之间均至少 有一条链,否则称作不连 通图。 连通分支: 支撑子图(生成子图): 如果 V2 = V1 , E2 E1 ,称 G2 是 G1 的 支撑子图(生成子图). 有向图相关概念 基础图:有向图中去掉所有弧上的箭头, 得到的无向图。 弧:有向图的边a=(u ,v),起点u,终点v; 路:若有从 u 到 v 不考虑方向的链,且 各方向一致,则称之为从u到v的路; 初等路: 各顶点都不相同的路; 初等回路:u = v 的初等路; 无向图中的概念总结 • 多重边 奇点 • 简单图 偶点 • 多重图 链 • 环 圈 • 次 初等(简单)链 • 悬挂点 初等(简单)圈 • 悬挂边 连通图 • 孤立点 支撑子图 v1 e1 e2 e3 e3 e4 e5 e6 v2 v3 v v4 v 5 6 无向图的性质 定理1 (握手定理)所有顶点次数之和等于所有边数 的2倍。 定理2 在任一图中,奇点的个数必为偶数。 以下各点能不能是某简单图的顶点的次的序列? (1)7,6,5,4,3,2 (2)6,6,5,4,3,2,1
6.2最小支撑树 [例们今有保气站A,将给一居民区供应煤气,居民区各用 本节主要内容: △ 树的性质 树的概念与性质 树:无圈连通图 (1)G为树: 例判断下面图形哪个是树 (2)G连通,且边数=点数.1 C温c命动后 (3)G无圈,且边数-点数1: (5)任意两个顶点之间恰有一条链。 △ 图的支撑树 定理3国G有支排树充要条件是图G是连通, (】南法 问题:如何找一个图的支掉树??? 在里搜接来步的雷串鞋包酱对途下的图 在该方法中,去掉的边戴为:边数点数+1 AN△ 4
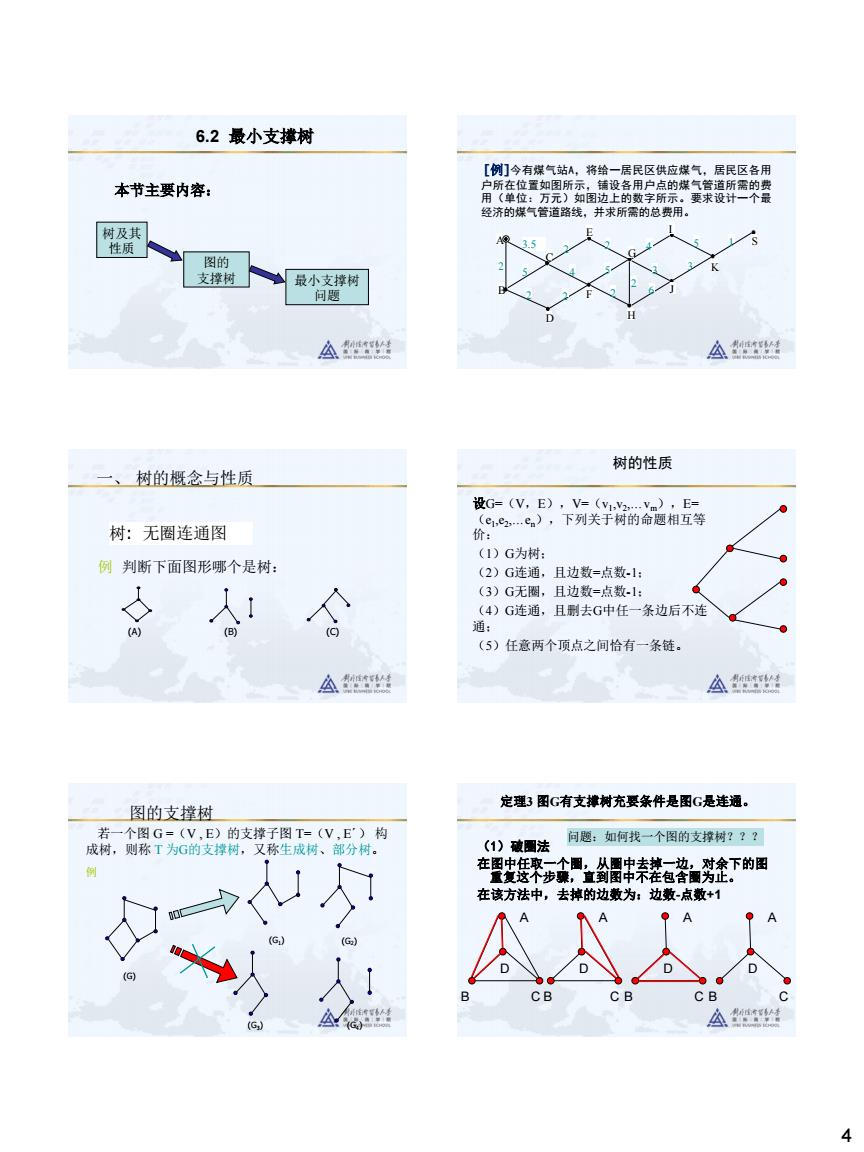
4 6.2 最小支撑树 本节主要内容: 树及其 性质 图的 支撑树 最小支撑树 问题 [例]今有煤气站A,将给一居民区供应煤气,居民区各用 户所在位置如图所示,铺设各用户点的煤气管道所需的费 用(单位:万元)如图边上的数字所示。要求设计一个最 经济的煤气管道路线,并求所需的总费用。 3.5 A B C D E F G H I J K S 2 2 2 2 2 2 5 4 5 2 6 3 4 5 3 1 树: 无圈连通图 (A) (B) (C) 例 判断下面图形哪个是树: 一、 树的概念与性质 树的性质 设G=(V,E),V=(v1 ,v2 ,…vm),E= (e1 ,e2 ,…en),下列关于树的命题相互等 价: (1)G为树; (2)G连通,且边数=点数-1; (3)G无圈,且边数=点数-1; (4)G连通,且删去G中任一条边后不连 通; (5)任意两个顶点之间恰有一条链。 若一个图 G =(V , E)的支撑子图 T=(V , E´) 构 成树,则称 T 为G的支撑树,又称生成树、部分树。 图的支撑树 (G) (G1 ) (G2 ) (G3 ) (G4 ) 例 定理3 图G有支撑树充要条件是图G是连通。 (1)破圈法 在图中任取一个圈,从圈中去掉一边,对余下的图 重复这个步骤,直到图中不在包含圈为止。 在该方法中,去掉的边数为:边数-点数+1 A B C D A B C D A B C D A B C D 问题:如何找一个图的支撑树???
(2)避圈法 二、最小支撑树问题 方法中 取出 图的所有树中权最小的树称为最小支撑树 公人 5 4 4 △ △ 求最小支撑树一避国法 求最小支撑树一破国法 以后每一步中 不含圈的图为止。 A性 △世 有想A。将给一民区应气。居民区 1 此即为最经济的煤气管道路线,所需的总费用为25万元 A整丝 A性
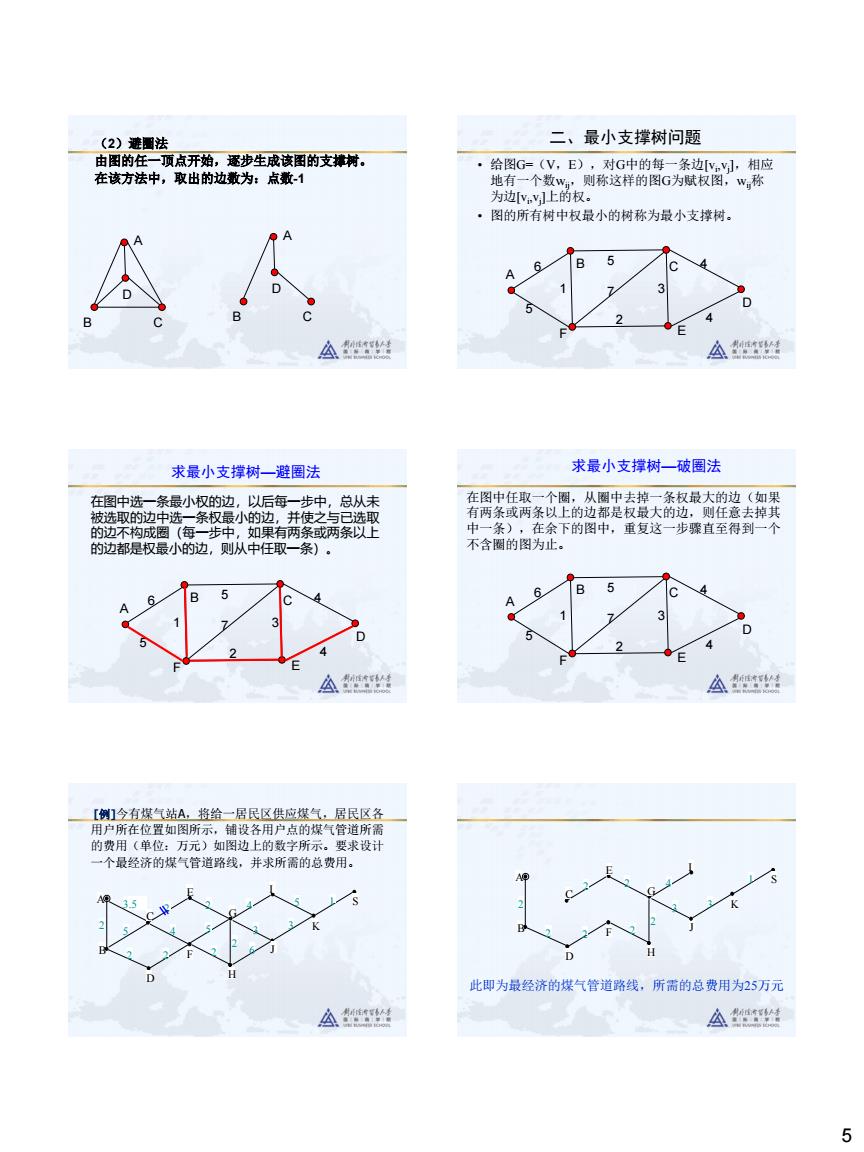
5 (2)避圈法 由图的任一顶点开始,逐步生成该图的支撑树。 在该方法中,取出的边数为:点数-1 A B C D A B C D 二、最小支撑树问题 • 给图G=(V,E),对G中的每一条边[vi ,vj ],相应 地有一个数wij,则称这样的图G为赋权图,wij称 为边[vi ,vj ]上的权。 • 图的所有树中权最小的树称为最小支撑树。 A B C D F E 6 5 1 5 7 2 3 4 4 求最小支撑树—避圈法 在图中选一条最小权的边,以后每一步中,总从未 被选取的边中选一条权最小的边,并使之与已选取 的边不构成圈(每一步中,如果有两条或两条以上 的边都是权最小的边,则从中任取一条)。 A B C D F E 5 1 2 3 6 5 7 4 4 求最小支撑树—破圈法 在图中任取一个圈,从圈中去掉一条权最大的边(如果 有两条或两条以上的边都是权最大的边,则任意去掉其 中一条),在余下的图中,重复这一步骤直至得到一个 不含圈的图为止。 A B C D F E 6 5 1 5 7 2 3 4 4 [例]今有煤气站A,将给一居民区供应煤气,居民区各 用户所在位置如图所示,铺设各用户点的煤气管道所需 的费用(单位:万元)如图边上的数字所示。要求设计 一个最经济的煤气管道路线,并求所需的总费用。 3.5 A B C D E F G H I J K S 2 2 2 2 2 2 5 4 5 2 6 3 4 5 3 1 I J A B C D E F G H K S 2 2 2 2 2 2 2 3 4 3 1 此即为最经济的煤气管道路线,所需的总费用为25万元