
2019/6/20 本章内容 第3章运输问题 3.1运输问题的数学模型 Transportation Problems 3.2表上作业法 3.3运输问题变形 马俊 3.4指派问题 国际商学院 2019-6-2 3.5运输问题的中转问题 △丝 A图 3.1运输问题的数学模型 简述 石8 单列章的原因在于: 方法对此类型进行求解 用出了赛 本章的重点在:掌提表格化方法求解运输 国B 产地产量 销量销地 A 3.1运输问题的数学模型 运输问线性规划模犁 数学篇器 B1 B2B3 B4 A A型性 1
2019/6/20 1 第3章 运输问题 Transportation Problems 马俊 国际商学院 2019-6-2 本章内容 3.1 运输问题的数学模型 3.2 表上作业法 3.3 运输问题变形 3.4 指派问题 3.5 运输问题的中转问题 • 运输、指派和转运问题,实际上都可以用 LP 模 型加以描述,所以可以认为它们是 LP 的特例 • 单列一章的原因在于:应用面极广,实践性很强, 而特有的数学结构使得人们设计出了特别有效的 方法对此类模型进行求解 • 本章的重点在:掌握表格化方法求解运输 简述 3.1 运输问题的数学模型 11 c 产地 产量 销地 1 a i a ma 1 b j b n b 1 j c i1 c ij c in c mn c mj c m1 c 1n c A1 Ai Am B1 Bj Bn 销量 3.1 运输问题的数学模型 例. 有A1,A2,A3三个砖瓦厂月产量分别为14,27,19 万块,供应B1,B2,B3,B4四个工地,月需要量分别为 22,13,12,13万块,每万块运费如下表,求总运费最 少的方案。 A1 14 A2 27 A3 19 22 13 12 13 B1 B2 B3 B4 6(千元) 7 5 3 8 4 2 7 5 9 10 6 运输问题线性规划模型 x x x x x x x x x x x x 0 x x x 13 x x x 12 x x x 13 x x x 22 x x x x 19 x x x x 27 s.t.x x x x 14 min z 6x 7x 5x 3x 8x 4x 2x 7x 5x 9x 10x 6x 11 12 13 14 21 22 23 24 31 32 33 34 14 24 34 13 23 33 12 22 32 11 21 31 31 32 33 34 21 22 23 24 11 12 13 14 11 12 13 14 21 22 23 24 31 32 33 34 + + = + + = + + = + + = + + + = + + + = + + + = = + + + + + + + + + + + 供 应 地 约 束 需 求 地 约 束

2019/6/20 运输问感模型与性质 运输问题的一般数学模型 ·运输问愿的一般提法:某种物资有若干产地和销 ·有m个产地生产某种物资,有个地区需要该类物资 地,现在需要把这种物资从各个产地运到各个销 ,b.bbn表示各销地 地,产量总数等于销量总数。已知各产地的产量 和各销地的销量以及各产地到各销地的单位运价 min w- ==2n销量约 A性 0 A 运输问惠的特点与性质 ◆矩阵的元素均为1或0: 存获组的矩库具有特珠的结构写出式系 。每一列只有两个元素为1,其余元素均为0: 0.10.0r,其 △世 3.2运输问题的表上作业法 运输问题的表上作业法 表上作业法和单纯形法的求解思想完全一数,但 是具体作法更加简德。 A整 A性 2
2019/6/20 2 运输问题模型与性质 • 运输问题的一般提法: 某种物资有若干产地和销 地,现在需要把这种物资从各个产地运到各个销 地,产量总数等于销量总数。已知各产地的产量 和各销地的销量以及各产地到各销地的单位运价 (或运距),问应如何组织调运,才能使总运费 (或总运输量)最省? 运输问题的一般数学模型 • 有m个产地生产某种物资,有n个地区需要该类物资 • 令a1 , a2 , …, am表示各产地产量, b1 , b2 , …, bn表示各销地 的销量,ai=bj称为产销平衡。 • 设xij表示产地 i 运往销地 j 的物资量,cij表示对应的单位 运费,则我们有运输问题的数学模型如下: = = = = = = = = = 0 1,2, , 1,2, , min 1 1 1 1 ij j m i ij n j ij i m i n j ij ij x x b j n x a i m w c x 销量约束 产地约束 运输问题的特点与性质 约束方程组的系数矩阵具有特殊的结构,写出式系 数矩阵A,形式如下: n n m m mn x , x , , x ; x , x , x , , , , , x , x , x 1 1 1 2 1 2 1 2 2 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 m行 n行 ❖ 矩阵的元素均为1或0; ❖ 每一列只有两个元素为1,其余元素均为0; ❖ 列向量Pij =(0,…,0,1,0,…,0,1,0,…0)T,其中 两个元素1分别处于第i行和第m+j行。 3.2 运输问题的表上作业法 (1)单纯形法 (2)表上作业法 由于问题的特殊形式而采用的更简洁、更方 便的方法。 运输问题的表上作业法 表上作业法的基本思想是:先设法给出一个初始方 案,然后根据确定的判别准则对初始方案进行检查、调 整、改进,直至求出最优方案,如图3-1所示。 表上作业法和单纯形法的求解思想完全一致,但 是具体作法更加简捷

2019/6/20 方 定是香 是 初始方案的确定 作业表(产销平衡表) 基本可行解) 初始方案戴是初始基本可行解, 格运输门愿的有关信息表和决策变量—澜运量结 最优方案 合在一起构成“作业表”(产销平衡表)。 表31是两个产地、三个销地的运输问题作业表。 图31运输问思求解思路图 A 例31甲、乙两个煤矿供应A、B、C三个城市用 表31运输间圆作麦(运价麦) 煤,各煤矿产量及各城市需煤量、各煤矿到各城市的 解地 运输距离见下表,求使总运输量最少的调运方案。 B: 产量 运距 城市 产地 A 250 日销量 6 (求量) 100 200 例3-1的数学模型 初始解的确定 mmZ=90x,+70x2+100x+80x1+65x2+752总运输量 1、最小元素法 景小元素法的基本思想是“就近供应”, ,+,+=200 ++=250日产量约束 2、西北角法 西北角法则不考感运距(或运价),年次部 需求约 选余表格的左上角(即西北角)元素作为基变 +5=20 量,其它过程与最小元素法相同 ,20,il2j-l23 A兰
2019/6/20 3 确定初始方案 ( 初 始 基本可行解) 改进调整 (换基迭代) 否 判定是否 最 优? 是 结 束 最优方案 图3-1 运输问题求解思路图 初始方案的确定 作业表(产销平衡表) 初始方案就是初始基本可行解。 将运输问题的有关信息表和决策变量——调运量结 合在一起构成“作业表”(产销平衡表)。 表3-1是两个产地、三个销地的运输问题作业表。 调 销地 运 量 产地 B1 B2 B3 产 量 A1 c11 X11 c12 X12 c13 X13 a1 A2 c21 X21 c22 X22 c23 X23 a2 销 量 b1 b2 b3 = = = 3 1 2 1 j j i i a b 表3-1 运输问题作业表(运价表) 例3-1 甲、乙两个煤矿供应A、B、C三个城市用 煤,各煤矿产量及各城市需煤量、各煤矿到各城市的 运输距离见下表,求使总运输量最少的调运方案。 100 150 200 450 日销量 (需求量) 乙 80 65 75 250 甲 90 70 100 200 日产量 A B C (供应量) 运距 城市 煤矿 例3-1的数学模型 = = + = + = + = + + = + + = = + + + + + 0, 1,2; 1,2,3; 200 150 100 250 200 . . min 90 70 100 80 65 75 1 3 2 3 1 2 2 2 1 1 2 1 2 1 2 2 2 3 1 1 1 2 1 3 1 1 1 2 1 3 2 1 2 2 2 3 x i j x x x x x x x x x x x x st Z x x x x x x ij 需求约束 日产量约束 总运输量 初始解的确定 1、最小元素法 最小元素法的基本思想是“就近供应” ; 2、西北角法 西北角法则不考虑运距(或运价),每次都 选剩余表格的左上角(即西北角)元素作为基变 量,其它过程与最小元素法相同

2019/6/20 用西北角法确定例31初始调运方案 用最小元素法确定例31初始调运方案 调、地 运 B B 产量 B B 产量 1009010-70: -00-280100 10090 79100100260100 A Xu X 80:506520075☐250200 89150第100752Q-100 A X2 100 10:200 销量 100 150 200 50 50 00 40,02 A 最优性检验 (一)闭回路法 检查当前调运方案是不是优方案的过程就是优性 什么是闭回略? 检查的万运 导于零,则该方案就是最优调运方案,否则就应 甲实的护钠的度一条封闭查镜。且所有的边部是水 (一)阳回略法 (二)对得变量法 △世 △世 (一)闭回略法 约定作为起始顶点的非基变量为奇数点1其它 以确定了初始调运方案的作业表为基赠,以一 项点顺次排列,那度,该非基变量x的检验数: 个非基变量作为起始顶点,寻求闭回略。 0,三(闭回略上奇数次顶点运距或运价之和) 可以证明。如果对闭同路的方向不加区别,对 (闭回略上偶囊次顶点运距或运价之和) A性 A性 d
2019/6/20 4 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 用最小元素法确定例3-1初始调运方案 150 100 100 100 100 100 100 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 用西北角法确定例3-1初始调运方案 100 100 100 50 50 200 200 得到初始调运方案为: x11=100,x12=100,x22=50,x23=200 检查当前调运方案是不是最优方案的过程就是最优性 检验。检查的方法:计算非基变量(未填上数值的格, 即空格)的检验数(也称为空格的检验数),若全部 大于等于零,则该方案就是最优调运方案,否则就应 进行调整。 (一)闭回路法 (二)对偶变量法 最优性检验 (一)闭回路法 什么是闭回路? 图中的折线构成一条封闭曲线,且所有的边都是水 平或垂直的; (a) (b) (c) (d) 以确定了初始调运方案的作业表为基础,以一 个非基变量作为起始顶点,寻求闭回路。 该闭回路的特点是:除了起始顶点是非基变量 外,其他顶点均为基变量(对应着填上数值的格)。 可以证明,如果对闭回路的方向不加区别,对 于每一个非基变量而言,以其为起点的闭回路存在 且唯一。 (一)闭回路法 约定作为起始顶点的非基变量为奇数点1 其它 顶点顺次排列,那麽,该非基变量xij的检验数: 现在,在用最小元素法确定例3-1初始调运方案的 基础上,计算非基变量X12的检验数 : ij =(闭回路上奇数次顶点运距或运价之和)- (闭回路上偶数次顶点运距或运价之和) (3-1)
2019/6/20 例31初始调运方案中以X,(为起点的闭回路 非基变量X的检验藏 丽地 ()-() B. 产量 =70+75(100+65)=-20, 10090 非基变量X的检验最: 200 0 15250 =80+100-(90+75)=15. 200 量 450 (二)位势法 例31初始调运方案位势变量对应表 地 B B2 品产 产地 10090 70100100200 6510075250 钠量 100 200450 位势变 △ (二)位势法 方程组的特点: 然后构造下面的方程组: ◆方程个数是mn12+31的 位势变量共有 41+y=G1=90 的券35个 通常称u为第行的位势,称v为第列 4,+y,=c,2=100 (32) ◆初始方室的每一个共变量x对应一个方程一所 42+2=c22=65 在行和列对应的位势变量之和等于该基变量对应的运 (4,+V3=c23=75 距(或运价):u+yFC ◆方程组恰有一个自由变量,可以证明方程组中任 意一个变量均可取作自由变量
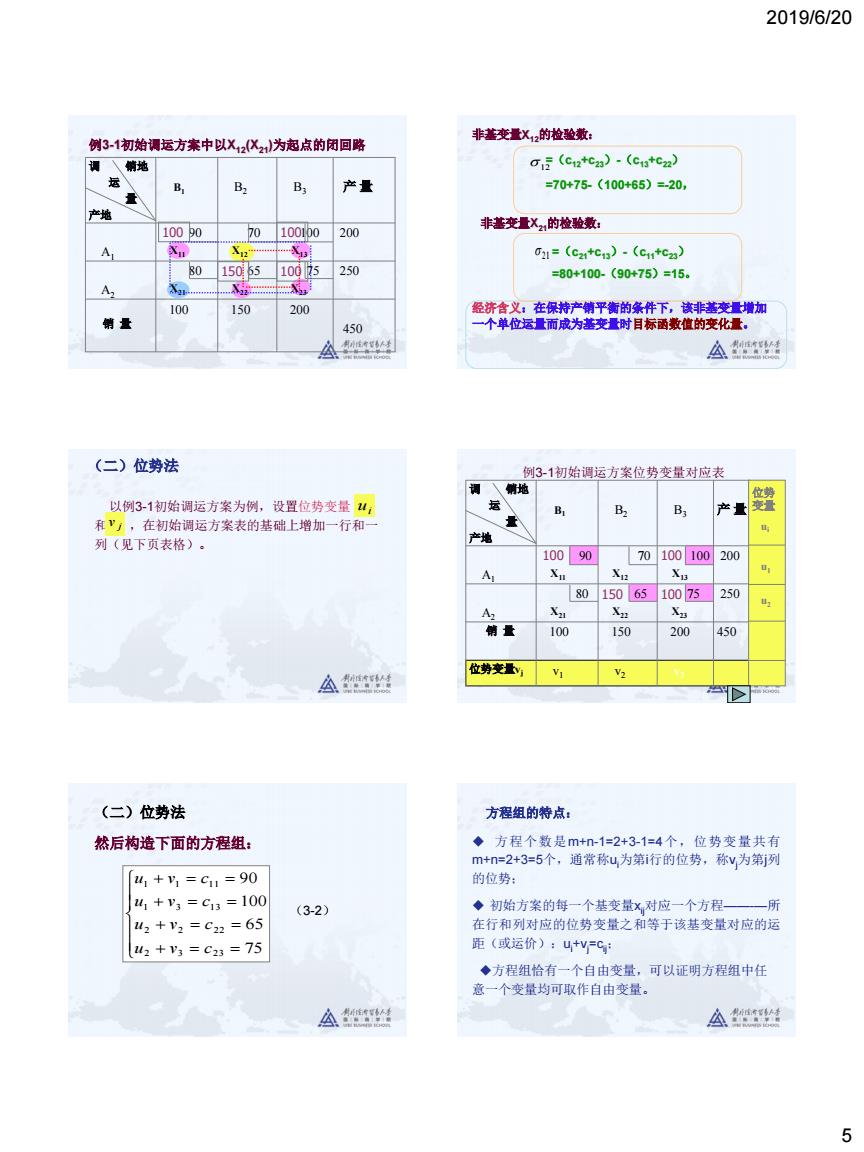
2019/6/20 5 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 100 100 150 100 例3-1初始调运方案中以X12(X21)为起点的闭回路 非基变量X12的检验数: 非基变量X21的检验数: =(c12+c23)-(c13+c22) =70+75-(100+65)=-20, 12 =(c21+c13)-(c11+c23) =80+100-(90+75)=15。 21 经济含义:在保持产销平衡的条件下,该非基变量增加 一个单位运量而成为基变量时目标函数值的变化量。 以例3-1初始调运方案为例,设置位势变量 和 ,在初始调运方案表的基础上增加一行和一 列(见下页表格)。 ui j v (二)位势法 例3-1初始调运方案位势变量对应表 调 销地 运 量 产地 B1 B2 B3 产 量 A1 90 X11 70 X12 100 X13 200 A2 80 X21 65 X22 75 X23 250 销 量 100 150 200 450 位势变量vj v1 v2 v3 100 100 150 100 位势 变量 ui u1 u2 (二)位势法 然后构造下面的方程组: + = = + = = + = = + = = 75 65 100 90 2 3 23 2 2 22 1 3 13 1 1 11 u v c u v c u v c u v c (3-2) 方程组的特点: ◆ 方程个数是m+n-1=2+3-1=4个,位势变量共有 m+n=2+3=5个,通常称ui为第i行的位势,称vj为第j列 的位势; ◆ 初始方案的每一个基变量xij对应一个方程——-—所 在行和列对应的位势变量之和等于该基变量对应的运 距(或运价):ui +vj =cij; ◆方程组恰有一个自由变量,可以证明方程组中任 意一个变量均可取作自由变量