
电路储能元件RL电路Ri(t >0)应用KVL和电感的VCR得:uRi +u, =u,(t)aldi=LRi+ Lu.=us(tdtdtR若以电感电压为变量Ldt +u = us(t)酒uLRdus(t)duULdtdt返上回页下页
( ) L S Ri + u = u t ( ) d d S u t t i Ri + L = 应用KVL和电感的VCR得: t i u L d d L = 若以电感电压为变量: d ( ) L L S u t u u t L R + = t u t t u u L R d d ( ) d d L S L + = 上 页 下 页 (t >0) + – Us uL R i + - RL电路 返 回

电路储能元件二图示为电容放电电路,电容原先带有电压U.求例3开关闭合后电容电压随时间的变化(t=0)Ri+u.=0(t≥0)解duRuc主RC'c+u=0dtp =-1/RC特征根方程:RCp+1=0RC通解:u.(t) = kept = keR→u(t)=Ue代入初始条件得:k=U在动态电路分析中,初始条件是得到明确确定解答的必需条件。返上回页F页
图示为电容放电电路,电容原先带有电压Uo ,求 开关闭合后电容电压随时间的变化。 例3 解 0 d d + c = c u t u RC Ri + u = 0 (t 0) c 特征根方程: RCp+1= 0 p = −1 RC 通解: U o k = RC t pt c u t ke ke − ( ) = = 代入初始条件得: RC t c o u t U e − ( ) = 在动态电路分析中,初始条件是得到 确定解答的必需条件。 上 页 下 页 明确 R - + C i uC (t=0) 返 回

电路储能元件②电容的初始条件i()d-01T" i()dEi()d +C-CJOi()d(0.)+一=uct = 0. 时刻1. i)duc(O+)=uc(0_)+/C Jo.当()为有限值时返上回页页F
( )d 1 ( ) − = t C i C u t ()d 1 ( )d 1 0 0 − − = + − t i C i C ()d 1 (0 ) 0− = − + t C i C u t = 0+时刻 ()d 1 (0 ) (0 ) 0 0 + − + = − + i C uC uC i uc C + - ②电容的初始条件 0 上 页 下 页 当i()为有限值时 返 回
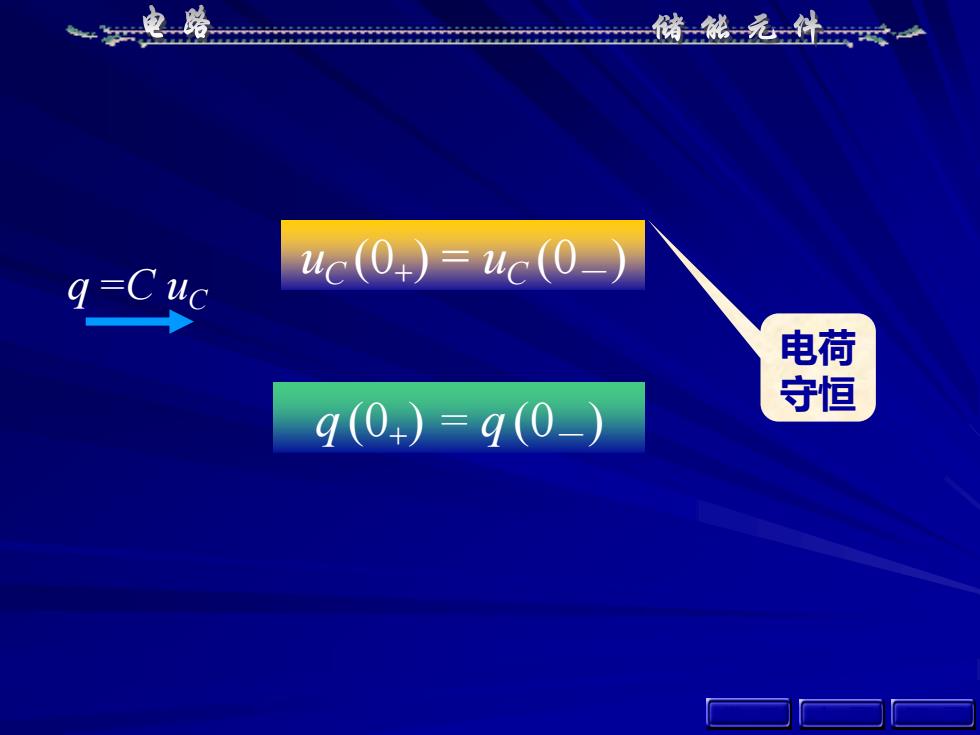
电路储能元件二uc(0+) = uc(0_)q=Cuc电荷守恒q(0+) =q(0_)
q (0+ ) = q (0-) uC (0+ ) = uC (0-) q=C uC 电荷 守恒 返 回 上 页 下 页
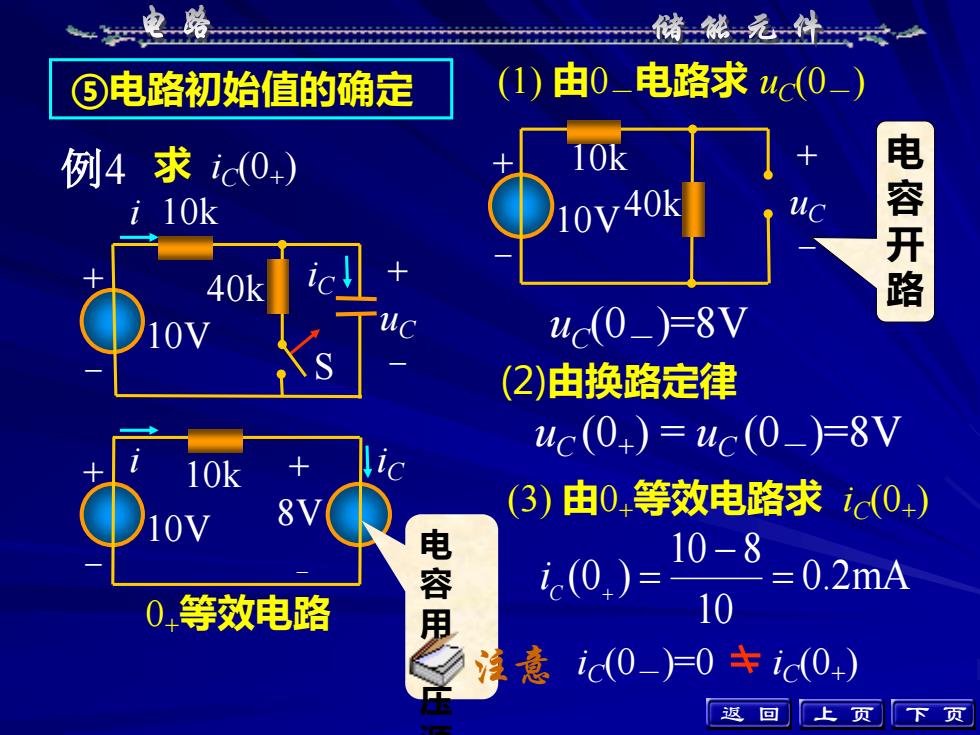
电路储能元件(1)由0_电路求 uc(0_)③电路初始值的确定电容开路10k例4 求ic(0)10v40ki 10k40kuc(0_)=8V10V(2)由换路定律uc(0+)= uc(0_)=8V+1O10k(3)由0.等效电路求ic(0+)8V10V电容用10-8=0.2mAic(0)100.等效电路ic(0_)=0 ± ic(0+)注意返上回页下页
⑤电路初始值的确定 (2)由换路定律 uC (0+ ) = uC (0-)=8V 0.2mA 10 10 8 (0 ) = − i C + = (1) 由0-电路求 uC(0-) uC (0-)=8V (3) 由0+等效电路求 iC(0+ ) iC(0-)=0 iC(0+ ) 例4 求 iC(0+ ) 电 容 开 路 上 页 下 页 + - 10V i iC + uC S - 10k 40k + - 10V + uC - 10k 40k + 8V - 0+等效电路 + - 10V i 10k iC 电 容 用 电 压 源 注意 返 回