
电路A教案 菲七章一阶电路和二阶电路 ug +uc=Us 方程c告+= K(0) 由初始条件4(0,)=0,得方程解: Us g 4,=U。-Ue嘉-U,1-e)(t≥0) 14c0门)=0 从上式可以得出电流: dt 从以上各式可以得出 (1)电压、电流是随时间按同一指数规律变化的函数,电容电压由两部分构成: 稳态分量(强制分量)+暂态分量(自由分量) (2)响应变化的快慢,由时间常数=RC决定:τ大,充电慢,T小充电就快。 (3)响应与外加激励成线性关系: (4)充电过程的能量关系为: 电容最终储存能量: 电源提供的能量为 W=J6tU,idt=U,9=CU月 电阻消耗的能量为: Wa=j6Rt=e子Rt 二、RL电路的零状态响应 用类似方法分析图所示的RL电路。电路在开关闭合前处于零初始状态,即电感 电流L(0)=0,开关闭合后,根据KCL、KVVL可得::+,=Ug K(F) 把 = L+Ri:=Us 代入上式得微分方程: dt 第6页共19页
电路 A 教案 第七章 一阶电路和二阶电路 第 6 页 共 19 页 方程 C C S du RC u U dt + = , 由初始条件 (0 ) 0 C u + = ,得方程解: 从上式可以得出电流: 从以上各式可以得出 (1)电压、电流是随时间按同一指数规律变化的函数,电容电压由两部分构成: 稳态分量(强制分量)+暂态分量(自由分量) (2)响应变化的快慢,由时间常数 τ= RC 决定;τ 大,充电慢,τ 小充电就快。 (3)响应与外加激励成线性关系; (4)充电过程的能量关系为: 电容最终储存能量: 电源提供的能量为: 电阻消耗的能量为: 二、RL 电路的零状态响应 用类似方法分析图所示的 RL 电路。电路在开关闭合前处于零初始状态,即电感 电流 iL(0-)=0 ,开关闭合后,根据 KCL、KVVL 可得: 把 代入上式得微分方程:
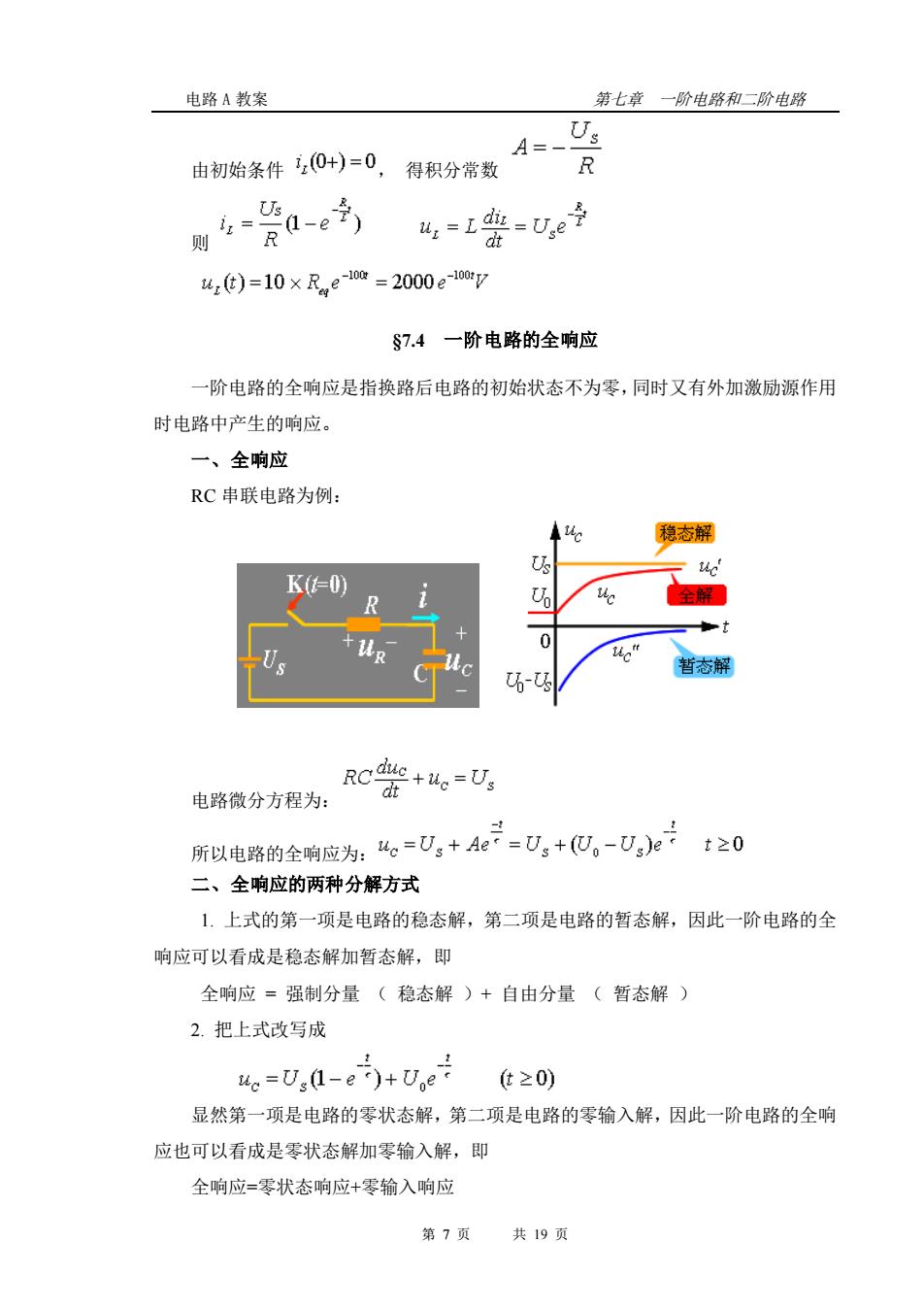
电路A教案 第七章一阶电路和二阶电路 由初始条件,0+)=0,得积分常数 A=_U R 用4-警0 4,=L=Ue子 4ze)=10×Rne-10e=2000e10e7 §7.4一阶电略的全响应 一阶电路的全响应是指换路后电路的初始状态不为零,同时又有外加激励源作用 时电路中产生的响应。 一、全响应 RC串联电路为例: 稳态解 暂态解 电路微分方程为: RC密+。=巧 所以电路的全响应为:4。=Ug+4e2=U,+心。-0,)e÷t≥0 二、全响应的两种分解方式 1.上式的第一项是电路的稳态解,第二项是电路的暂态解,因此一阶电路的全 响应可以看成是稳态解加暂态解,即 全响应=强制分量(稳态解)+自由分量(暂态解) 2.把上式改写成 uc=U:(-ei)+Ue t20) 显然第一项是电路的零状态解,第二项是电路的零输入解,因此一阶电路的全响 应也可以看成是零状态解加零输入解,即 全响应=零状态响应+零输入响应 第7页共19页
电路 A 教案 第七章 一阶电路和二阶电路 第 7 页 共 19 页 由初始条件 , 得积分常数 则 §7.4 一阶电路的全响应 一阶电路的全响应是指换路后电路的初始状态不为零,同时又有外加激励源作用 时电路中产生的响应。 一、全响应 RC 串联电路为例: 电路微分方程为: 所以电路的全响应为: 二、全响应的两种分解方式 1. 上式的第一项是电路的稳态解,第二项是电路的暂态解,因此一阶电路的全 响应可以看成是稳态解加暂态解,即 全响应 = 强制分量 ( 稳态解 )+ 自由分量 ( 暂态解 ) 2. 把上式改写成 显然第一项是电路的零状态解,第二项是电路的零输入解,因此一阶电路的全响 应也可以看成是零状态解加零输入解,即 全响应=零状态响应+零输入响应