MO *f +42) 天→ -2/T -1/T 0 1/T 2/T IMOI 人人人八入 6
6 f fs - 2 / T - 1 / T 0 1 / T 2 / T (f) f -fH 0 fH fs |Ms(f)| -fH fH f |M(f)|

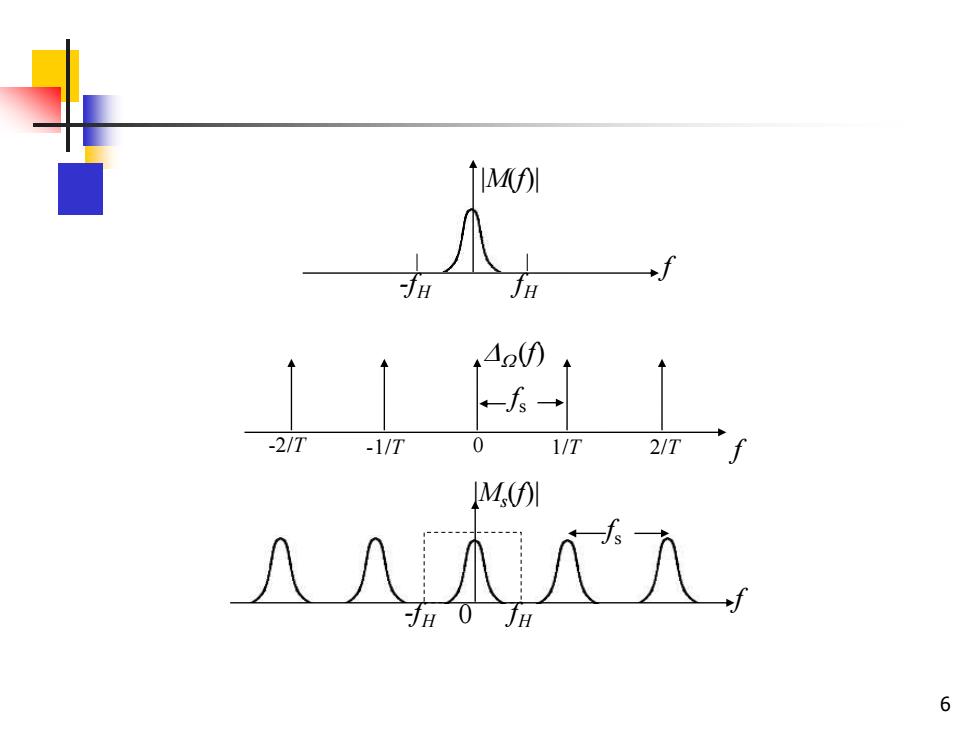
恢复原信号的方法:从上图可以看出,当f≥2时,用一个 截止频率为f的理想低通滤波器就能够从抽样信号中分离出 原信号。从时域中看,当用抽样脉冲序列冲激此理想低通滤 波器时,滤波器的输出就是一系列冲激响应之和,如下图所 示。这些冲激响应之和就构成了原信号。 理想滤波器是不能实现的。实用滤波器的截止边缘不可能做 到如此陡峭。所以,实用的抽样频率必须比2f大一些。 例如,典型电话信号的最高频率通常限制在3400Hz,而抽 样频率通常采用8000Hz。 7
7 恢复原信号的方法:从上图可以看出,当fs 2fH时,用一个 截止频率为fH的理想低通滤波器就能够从抽样信号中分离出 原信号。从时域中看,当用抽样脉冲序列冲激此理想低通滤 波器时,滤波器的输出就是一系列冲激响应之和,如下图所 示。这些冲激响应之和就构成了原信号。 理想滤波器是不能实现的。实用滤波器的截止边缘不可能做 到如此陡峭。所以,实用的抽样频率fs必须比2fH 大一些。 例如,典型电话信号的最高频率通常限制在3400 Hz,而抽 样频率通常采用8000 Hz。 t
带通抽样定理 信号频谱范围f~H 抽样频率f、应满足 fs =2B(1+k/n) B=fu-f n<fu/B的最大整数 k-fu/B-n 0≤k<1
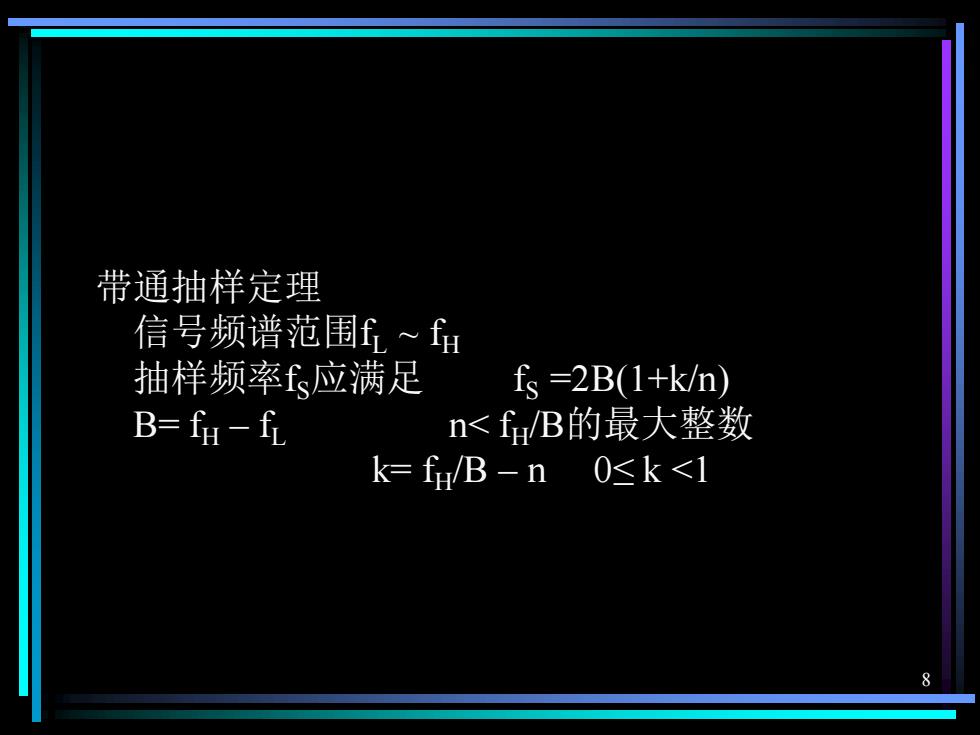
8 带通抽样定理 信号频谱范围fL ~ fH 抽样频率fS应满足 fS =2B(1+k/n) B= fH – fL n< fH/B的最大整数 k= fH/B – n 0≤ k <1

4B n= n=2 n=3 n=4 B 2B 3B 4B fs =2B(1+k/n) f0→B fHB→2B n=1 fB→2B f12B-→3B n=2 带通信号的抽样频率在2B至4B间变动
9 2B 4B S f L f B 2B 3B 4B n =1 n = 2 n = 3 n = 4 fS =2B(1+k/n) fL 0→B fH B→2B n=1 fL B→2B fH 2B→3B n=2 . 带通信号的抽样频率在2B至4B间变动

带通抽样定理在频域上的理解 以、=2B抽样,抽样后,各段频谱之间 不会发生混叠,采用带通滤波器,仍可 无失真地恢复原始信号
10 • 例 若fH = 3B 按低通抽样定理,则要求 fS≥6B 若fS=2B, 怎样? M () ( ) M −S ( ) M +S 带通抽样定理在频域上的理解 以 fs=2B抽样,抽样后,各段频谱之间 不会发生混叠,采用带通滤波器,仍可 无失真地恢复原始信号