
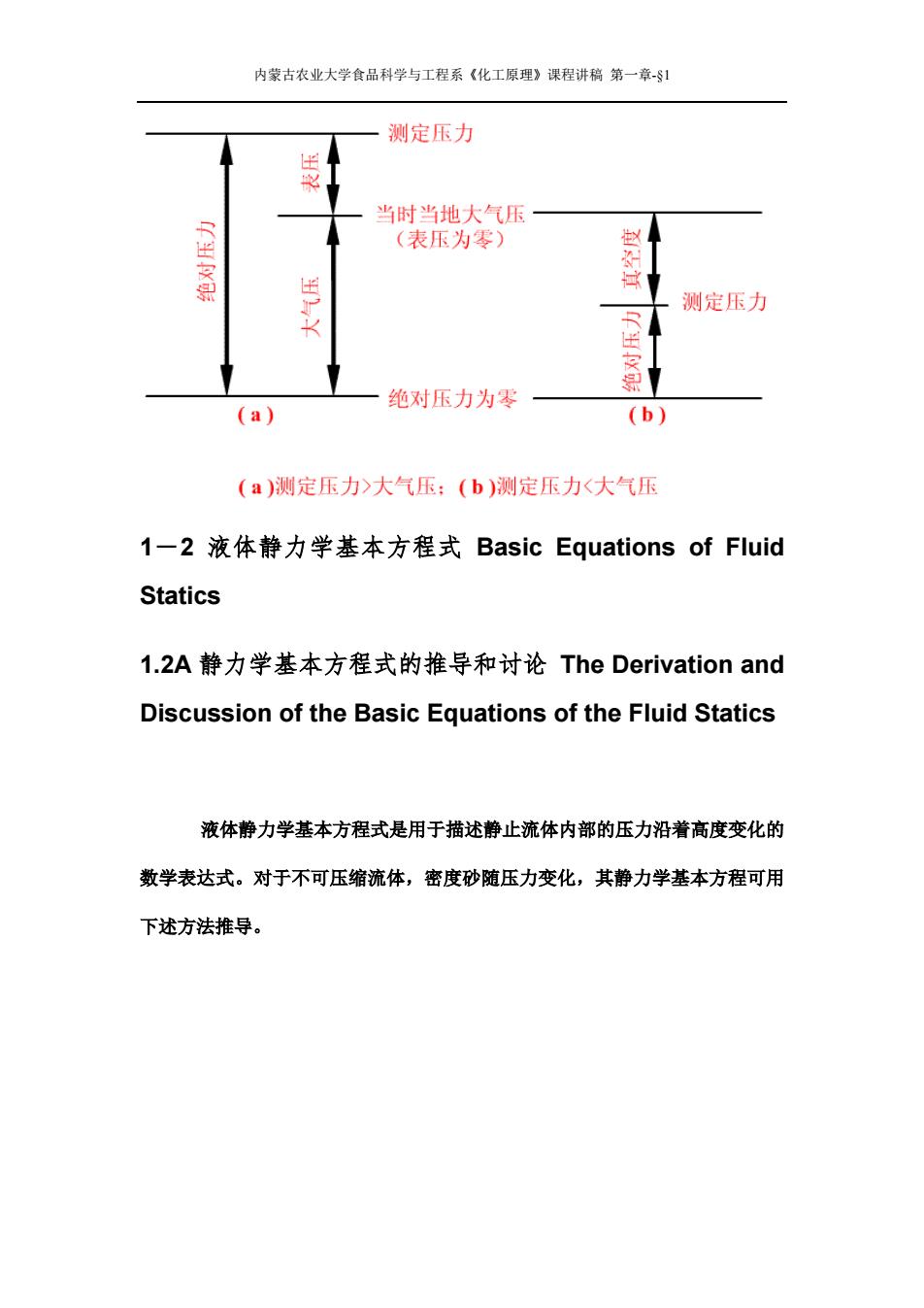
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 为压力。作用于整个面上的力称为总压力。在静止流体中,从各方向作用于某 一点的压力大小均相等。 在法定单位制中,压力的单位是 N/m2 ,称为帕斯卡,以 Pa 表示。但长期 以来采用的单位为 atm(标准大气压)、某流体在柱高度、bar(巴)或 kgf/cm2 等。它们之间的换算关系为: 1 标准大气压(atm)=101300Pa =10330kgf/m2 =1.033kgf/cm2 =10.33mH2O =760mmHg 压力可以有不同的计量基准: 如以绝对真空(即零大气压)为基准,称为绝对压力(absolute pressure)。 如以当地大气压为基准,则称为表压(gauge pressure)。 它与绝对压力的关系,可用下式表示 表压=绝对压力-大气压力 (1—9) 当被测流体的绝对压力小于大气压时,其低于大气压的数值称为真空度 (vacuum),即 真空度=大气压力-绝对压力 (1—10) 注意,此处的大气压力均应指当地大气压。在本章中如不加说明时均可按 标准大气压计算。 绝对压力、表压和真空度的关系,如图 1-1 所示。 例 1-3 某台离心泵进、出口压力表读数分别为 220mmHg(真空度)及
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 为压力。作用于整个面上的力称为总压力。在静止流体中,从各方向作用于某 一点的压力大小均相等。 在法定单位制中,压力的单位是 N/m2 ,称为帕斯卡,以 Pa 表示。但长期 以来采用的单位为 atm(标准大气压)、某流体在柱高度、bar(巴)或 kgf/cm2 等。它们之间的换算关系为: 1 标准大气压(atm)=101300Pa =10330kgf/m2 =1.033kgf/cm2 =10.33mH2O =760mmHg 压力可以有不同的计量基准: 如以绝对真空(即零大气压)为基准,称为绝对压力(absolute pressure)。 如以当地大气压为基准,则称为表压(gauge pressure)。 它与绝对压力的关系,可用下式表示 表压=绝对压力-大气压力 (1—9) 当被测流体的绝对压力小于大气压时,其低于大气压的数值称为真空度 (vacuum),即 真空度=大气压力-绝对压力 (1—10) 注意,此处的大气压力均应指当地大气压。在本章中如不加说明时均可按 标准大气压计算。 绝对压力、表压和真空度的关系,如图 1-1 所示。 例 1-3 某台离心泵进、出口压力表读数分别为 220mmHg(真空度)及

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1.7kgf/cm2 (表压)。若当地大气压力为 760mmHg,试求它们的绝对压力各为若干 (以法定单位表示)? 解 泵进口绝对压力 P1=760-220=540mmHg =7.2x104 Pa 泵出口绝对压力 P2=1.7+1.033 =2.733kgf/cm2 =2.68x105 Pa
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1.7kgf/cm2 (表压)。若当地大气压力为 760mmHg,试求它们的绝对压力各为若干 (以法定单位表示)? 解 泵进口绝对压力 P1=760-220=540mmHg =7.2x104 Pa 泵出口绝对压力 P2=1.7+1.033 =2.733kgf/cm2 =2.68x105 Pa
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1-2 液体静力学基本方程式 Basic Equations of Fluid Statics 1.2A 静力学基本方程式的推导和讨论 The Derivation and Discussion of the Basic Equations of the Fluid Statics 液体静力学基本方程式是用于描述静止流体内部的压力沿着高度变化的 数学表达式。对于不可压缩流体,密度砂随压力变化,其静力学基本方程可用 下述方法推导
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 1-2 液体静力学基本方程式 Basic Equations of Fluid Statics 1.2A 静力学基本方程式的推导和讨论 The Derivation and Discussion of the Basic Equations of the Fluid Statics 液体静力学基本方程式是用于描述静止流体内部的压力沿着高度变化的 数学表达式。对于不可压缩流体,密度砂随压力变化,其静力学基本方程可用 下述方法推导

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 现从静止液体中任意划出一垂直液柱,如图 1-2 所示。液柱的横截面积 为 A,液体密度为 ρ,若以容器器底为基准水平面,则液柱的上、下底面与基准 水平面的垂直距离分别为 Z1 和 Z2,以 p1与 p2 分别表示高度为 Z1 及 Z2处的压 力。 在垂直方向上作用于液柱的力有: 下底面所受之向上总压力为 p2A; 上底面所受之向下总压力为 p1A; 整个液柱之 G=ρgA(Z1-Z2)。 在静止液体中,上述三力之合力应为零,即 p2A-p1A-ρgA(Z1-Z2)=0 此式中向上的力用正号,向下的力用负号。化简并消去 A,得 p2=p1+ρg(Z1-Z2) (1-10) 如果将液柱的上底面取在液面上,设液面上方的压力为 p0,液柱 Z1-Z2=h, 则上式可改写为 p2=p0+ρgh (1-11) 式(1-10)及(1-11)称为静力学基本方程式
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 现从静止液体中任意划出一垂直液柱,如图 1-2 所示。液柱的横截面积 为 A,液体密度为 ρ,若以容器器底为基准水平面,则液柱的上、下底面与基准 水平面的垂直距离分别为 Z1 和 Z2,以 p1与 p2 分别表示高度为 Z1 及 Z2处的压 力。 在垂直方向上作用于液柱的力有: 下底面所受之向上总压力为 p2A; 上底面所受之向下总压力为 p1A; 整个液柱之 G=ρgA(Z1-Z2)。 在静止液体中,上述三力之合力应为零,即 p2A-p1A-ρgA(Z1-Z2)=0 此式中向上的力用正号,向下的力用负号。化简并消去 A,得 p2=p1+ρg(Z1-Z2) (1-10) 如果将液柱的上底面取在液面上,设液面上方的压力为 p0,液柱 Z1-Z2=h, 则上式可改写为 p2=p0+ρgh (1-11) 式(1-10)及(1-11)称为静力学基本方程式

内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 将式(1—10)移项得: (1—12) 1 1 2 2 p + ρgz = p + ρgz 式(1—12)各项除以密度 ρ ,可得: 2 2 1 1 gz p gz p + = + ρ ρ (1—13) 式(1—13)各项除以重力加速度 g,可得: 2 2 1 1 z g p z g p + = + ρ ρ (1—14) 讨论: 上述式(1—10) 至。(1—14)为液体静力学基本方程的各种形式。现作如下说 明和讨论: (1)上述流体静力学基本方程各种表达式只适用于重力场中静止的不可 压缩的连续的单一流体。 (2)式(1—11)表明,处于重力场中的流体的静压 p 的大小与流体本身的密度 和垂直位置有关,而与各点的水平位置无关。换句话说,在静止的连续的同 一液体中,处在同一水平位置上 的各点的压力都相等。 ρ 当液面的上方压力 p0 有变化时,必将引起液体内部各点压力发生同样大小 的变化。这就是巴斯噶原理。 (3)式(1—13)中各项的单位是 J/kg,为 1kg 流体具有的能量。其中, ρ p 称 为静压能,gz 为位能。可见,在静止流体中,一处静压能与位能之和等于另一 处静压能与位能之和。静压能和位能都属于机械能。静力学基本方程表明,在 静止流体中,这两种机械能之和是守恒的。 (4)式(1—12)中各项的单位为 Pa,亦即是 J/m3 。各项表示单位体积流体
内蒙古农业大学食品科学与工程系《化工原理》课程讲稿 第一章-§1 将式(1—10)移项得: (1—12) 1 1 2 2 p + ρgz = p + ρgz 式(1—12)各项除以密度 ρ ,可得: 2 2 1 1 gz p gz p + = + ρ ρ (1—13) 式(1—13)各项除以重力加速度 g,可得: 2 2 1 1 z g p z g p + = + ρ ρ (1—14) 讨论: 上述式(1—10) 至。(1—14)为液体静力学基本方程的各种形式。现作如下说 明和讨论: (1)上述流体静力学基本方程各种表达式只适用于重力场中静止的不可 压缩的连续的单一流体。 (2)式(1—11)表明,处于重力场中的流体的静压 p 的大小与流体本身的密度 和垂直位置有关,而与各点的水平位置无关。换句话说,在静止的连续的同 一液体中,处在同一水平位置上 的各点的压力都相等。 ρ 当液面的上方压力 p0 有变化时,必将引起液体内部各点压力发生同样大小 的变化。这就是巴斯噶原理。 (3)式(1—13)中各项的单位是 J/kg,为 1kg 流体具有的能量。其中, ρ p 称 为静压能,gz 为位能。可见,在静止流体中,一处静压能与位能之和等于另一 处静压能与位能之和。静压能和位能都属于机械能。静力学基本方程表明,在 静止流体中,这两种机械能之和是守恒的。 (4)式(1—12)中各项的单位为 Pa,亦即是 J/m3 。各项表示单位体积流体