
Nonlinear Equations →Motivation ●Bisection Method ·Newton's Method ·Secant Method ●Summary Copyright©2011,NA⊙Yin Last Modification:Oct.2011 2
Nonlinear Equations ⇒ Motivation • Bisection Method • Newton’s Method • Secant Method • Summary Copyright c 2011, NA Yin Last Modification: Oct. 2011 2

Motivation .For a given function f(),find its root(s),i.e.: =find x (or r=root)such that f(x)=0 ·BVP:dipping of suspended power cable.What isλ? 入cosh 50-λ-10=0 (Some)simple equations=solve analytically 6x2-7x+2=0c0s3x-c0s7x=0 (3x-2)(2x-1)=02sin5xsin2x=0 x= x=,暨,n∈Z Copyright©2011,NAOYin Last Modification:Oct.2011 3
Motivation • For a given function f(x), find its root(s), i.e.: ⇒ find x (or r=root) such that f(x) = 0 • BVP: dipping of suspended power cable. What is λ? λ cosh 50 λ − λ − 10 = 0 • (Some) simple equations ⇒ solve analytically 6x 2 − 7x + 2 = 0 cos 3x − cos 7x = 0 (3x − 2)(2x − 1) = 0 2 sin 5x sin 2x = 0 x = 2 3 , 1 2 x = nπ 5 , nπ 2 , n ∈ Z Copyright c 2011, NA Yin Last Modification: Oct. 2011 3

Motivation(cont.) In genetal,we cannot exploit the function,e.g.: 22-10x+1=0 and cosh(Vz2+1-e)+log sinx=0 Note:at times 3 multiple roots e.g.,previous parabola and cosine we want at least one we may only get one(for each search) Need a general,function-independent algorithm. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 4
Motivation(cont.) • In genetal, we cannot exploit the function, e.g.: 2 x 2 − 10x + 1 = 0 and cosh(p x 2 + 1 − e x ) + log |sin x| = 0 • Note: at times ∃ multiple roots ∗ e.g., previous parabola and cosine ∗ we want at least one ∗ we may only get one(for each search) Need a general, function-independent algorithm. Copyright c 2011, NA Yin Last Modification: Oct. 2011 4

Nonlinear Equations ●Motivation →Bisection Method ●Newton's Method ·Secant Method Summary Copyright 2011,NAOYin Last Modification:Oct.2011 5
Nonlinear Equations • Motivation ⇒ Bisection Method • Newton’s Method • Secant Method • Summary Copyright c 2011, NA Yin Last Modification: Oct. 2011 5
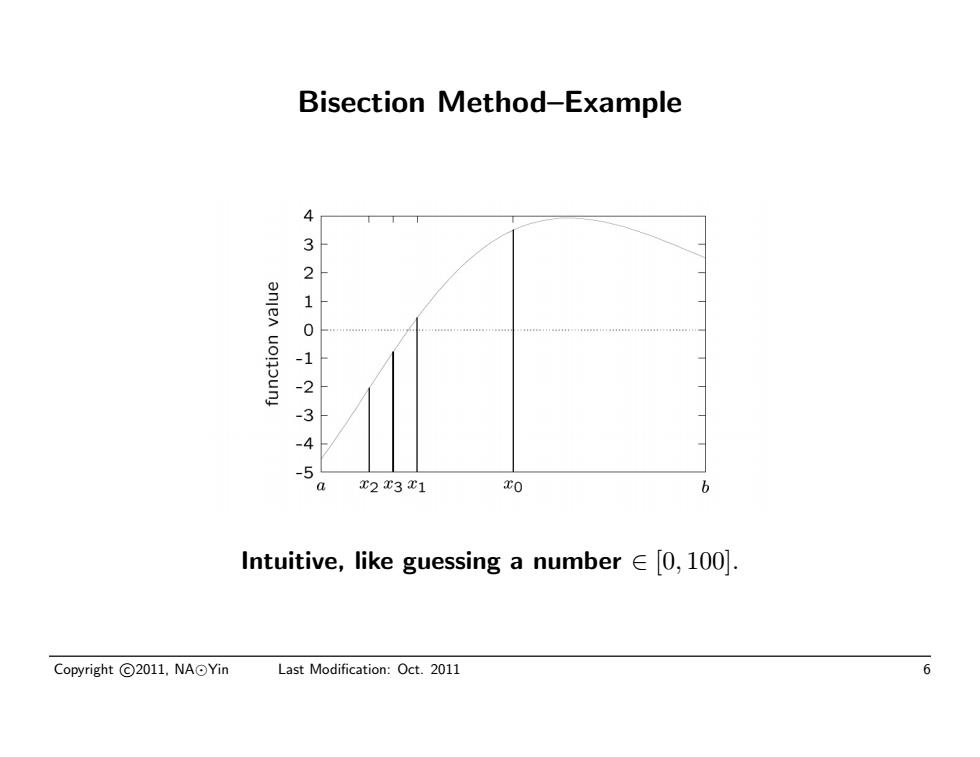
Bisection Method-Example 3 2 anjen uonounj 1 0 -1 -3 -4 -5 T2 43 1 0 b Intuitive,like guessing a number∈[0,l00l. Copyright©2011,NA⊙Yin Last Modification:Oct.2011 6
Bisection Method–Example Intuitive, like guessing a number ∈ [0, 100]. Copyright c 2011, NA Yin Last Modification: Oct. 2011 6