
Numerical Quadrature →Introduction ●Riemann Integration .Composite Trapezoid Rule Composite Simpson's Rule ●Gaussian Quadrature Copyright©2011NA⊙Yin 2
Numerical Quadrature ⇒ Introduction • Riemann Integration • Composite Trapezoid Rule • Composite Simpson’s Rule • Gaussian Quadrature Copyright c 2011 NA Yin 2
Numerical Quadrature -Interpretation f()>on [a,]boundedf()da is area under f() anjen uonounj b Copyright©2011NA⊙Yin 3
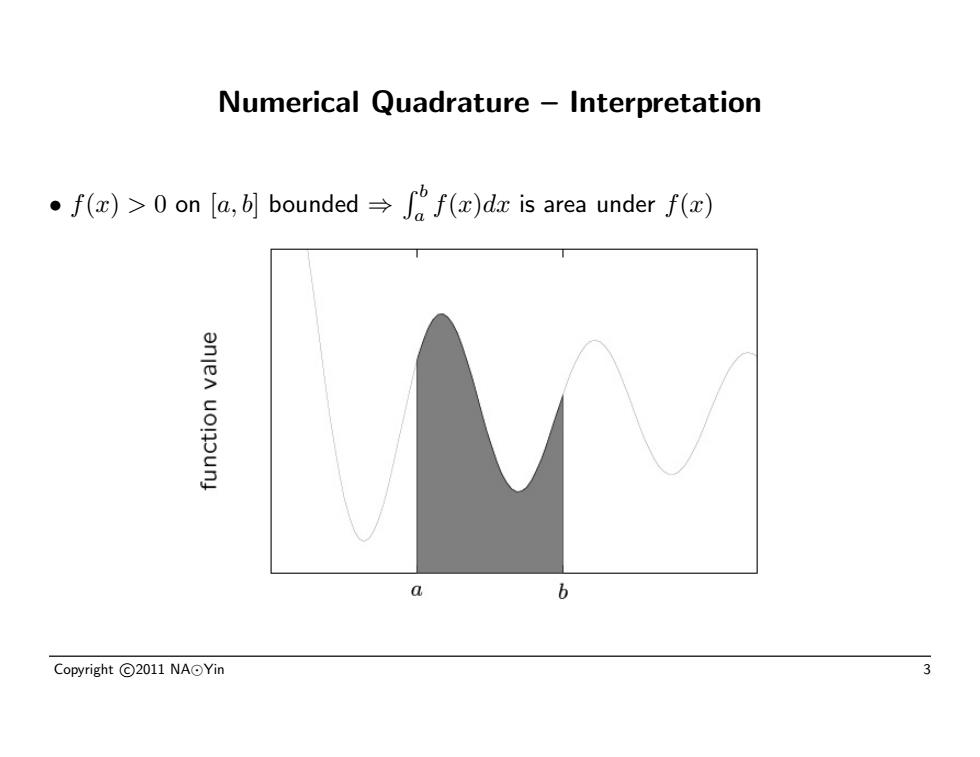
Numerical Quadrature – Interpretation • f(x) > 0 on [a, b] bounded ⇒ R b a f(x)dx is area under f(x) Copyright c 2011 NA Yin 3

Motivation Analytical solution-rare rπ/ sin(c)dr=-cosx6/2=-(0-1)=1 ●In general: π/2 (1-a2sin20)1/3d0 o e da Need general numerical technique Copyright 2011 NAOYin 4
Motivation • Analytical solution – rare Z π/2 0 sin(x)dx = − cos x| π/2 0 = −(0 − 1) = 1 • In general: Z π/2 0 (1 − a 2 sin2 θ) 1/3 dθ Z 1 0 e −x 2 dx Need general numerical technique Copyright c 2011 NA Yin 4

Definitions ●Mesh:P≡{a=xo<x1<·<xn=b},n subintervals(n+1 points) ●Infima and superma: m=inf{f(c):xa≤x≤x+1} M≡sup{f(x):x≤x≤c+1} Two methods(i.e.,integral estimates):lower and upper sums n1 f,P)=∑m,(1-x) i=0 Copyright©2011NA⊙Yin 5
Definitions • Mesh: P ≡ {a = x0 < x1 < · · · < xn = b}, n subintervals (n + 1 points) • Infima and superma: mi ≡ inf{f(x) : xi ≤ x ≤ xi+1} Mi ≡ sup{f(x) : xi ≤ x ≤ xi+1} • Two methods (i.e., integral estimates): lower and upper sums L(f, P) ≡ n X−1 i=0 mi(xi+1 − xi) Copyright c 2011 NA Yin 5

n-1 U(f,P)≡ Mi(xi+1-xi) i=0 ●For example Copyright©2011NA⊙Yin 6
U(f, P) ≡ n X−1 i=0 Mi(xi+1 − xi) • For example Copyright c 2011 NA Yin 6