
Approximation by Splines →Motivation ●Linear Splines ●Quadratic Splines ●Cubic Splines ●Summary Copyright©2011NA⊙Yin 1
Approximation by Splines ⇒ Motivation • Linear Splines • Quadratic Splines • Cubic Splines • Summary Copyright c 2011 NA Yin 1
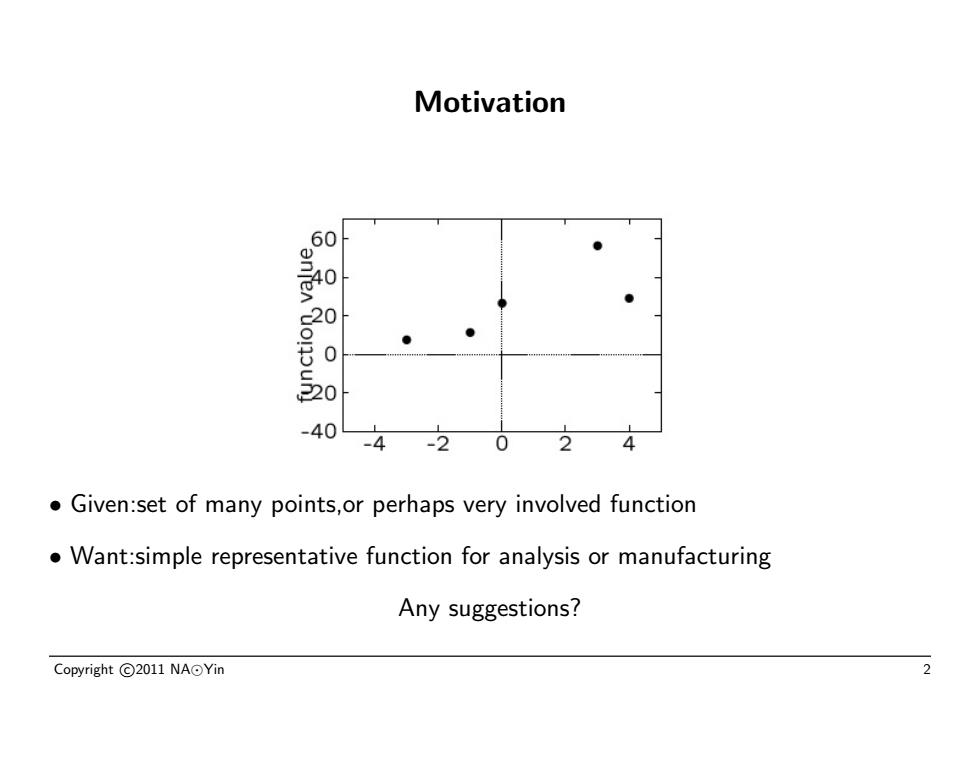
Motivation ● -40 -4-2 0 2 Given:set of many points,or perhaps very involved function Want:simple representative function for analysis or manufacturing Any suggestions? Copyright©2011NA⊙Yin 2
Motivation • Given:set of many points,or perhaps very involved function • Want:simple representative function for analysis or manufacturing Any suggestions? Copyright c 2011 NA Yin 2
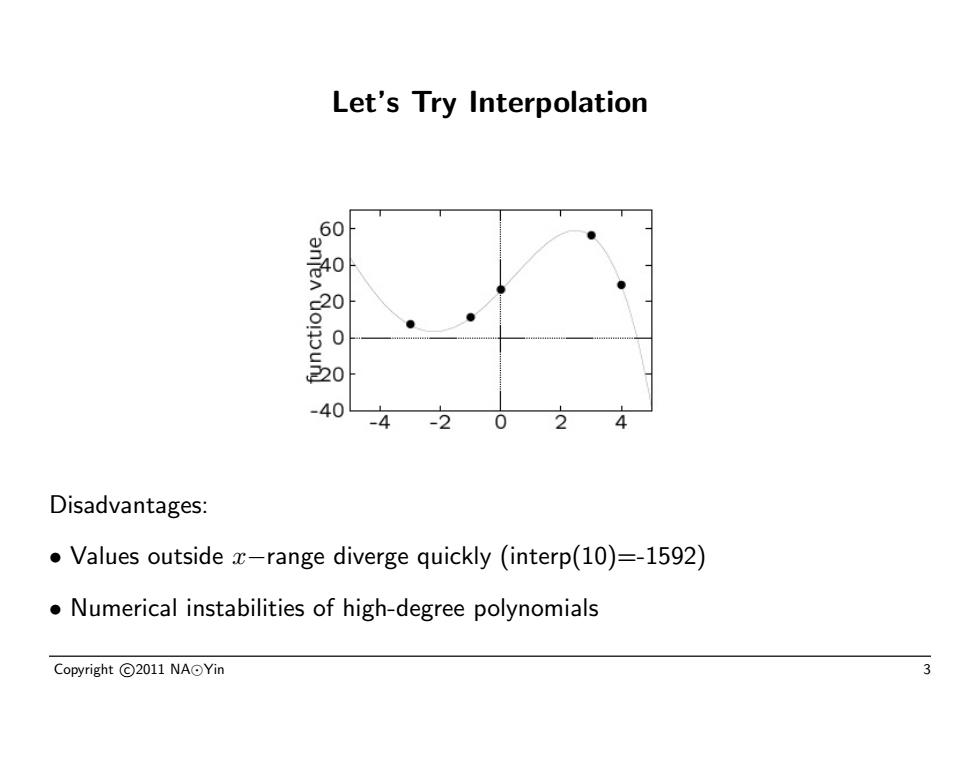
Let's Try Interpolation -40 -4 -2 0 Disadvantages: Values outside x-range diverge quickly (interp(10)=-1592) Numerical instabilities of high-degree polynomials Copyright©2011NA⊙Yin 3
Let’s Try Interpolation Disadvantages: • Values outside x−range diverge quickly (interp(10)=-1592) • Numerical instabilities of high-degree polynomials Copyright c 2011 NA Yin 3
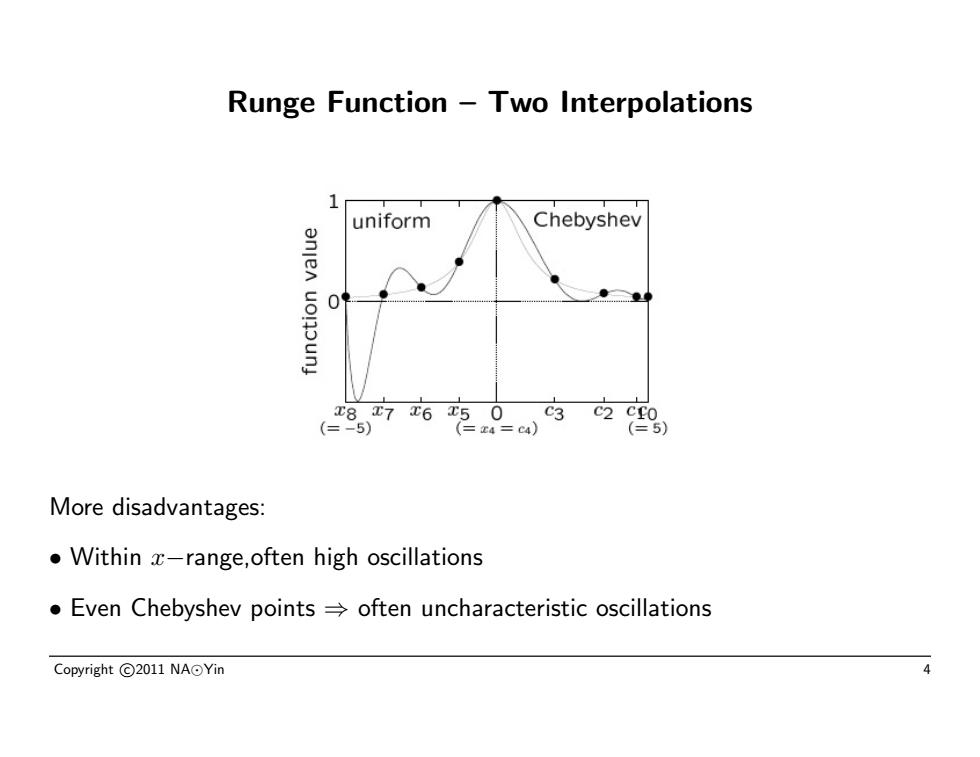
Runge Function-Two Interpolations 1 uniform Chebyshev anjen 8.7650、c3c2C0 (=-5) (x4=c4) (=5) More disadvantages: .Within x-range,often high oscillations Even Chebyshev points=often uncharacteristic oscillations Copyright©2011NA⊙Yin 4
Runge Function – Two Interpolations More disadvantages: • Within x−range,often high oscillations • Even Chebyshev points ⇒ often uncharacteristic oscillations Copyright c 2011 NA Yin 4

Splines Given domain [a,b],a spline S(x) Is defined on entire domain Provides a certain amount of smoothness 3partition of"knots"(=where spline can change form) {a to,t1,t2;...:tn=bh such that So(x),x∈[to,t], S(x)= S(x),x∈[t1,t2], Sn-1(x),x∈[tn-1,tn] is piecewise polynomial Copyright 2011 NAOYin 5
Splines Given domain [a, b],a spline S(x) • Is defined on entire domain • Provides a certain amount of smoothness • ∃ partition of ”knots”(=where spline can change form) {a = t0, t1, t2, . . . , tn = b} such that S(x) = S0(x), x ∈ [t0, t1], S1(x), x ∈ [t1, t2], ... Sn−1(x), x ∈ [tn−1, tn] is piecewise polynomial Copyright c 2011 NA Yin 5