
(1)在闭区间[a,b]上连续 fx) 件 (2)在开区间(4,b)内可导 满足 (3)a)=fb) 35∈(a,b 论 0 使得 =f'(5)(b-) 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 f b f a ( ) ( ) − = f ( ) ( ) b a − 满足 条 件 结 论 (3) f(a)=f(b) 0

(1)在闭区间[4,b]上连续 fx) 件 满足 (2)在开区间(4,b)内可导 (3)fa)=fb) 35∈(a,b 论 使得 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 满足 条 件 结 论 (3) f(a)=f(b)

(1)在闭区间[a,b]上连续 fx) 件 (2)在开区间(a,b)内可导 满足 (3)a)=fb) 35∈(a,b) 论 使得 5)=0 推广 罗尔定理 特 例 拉氏定理
罗尔定理 拉氏定理 推 广 特 例 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 满足 条 件 结 论 (3) f(a)=f(b) f ( ) 0 =
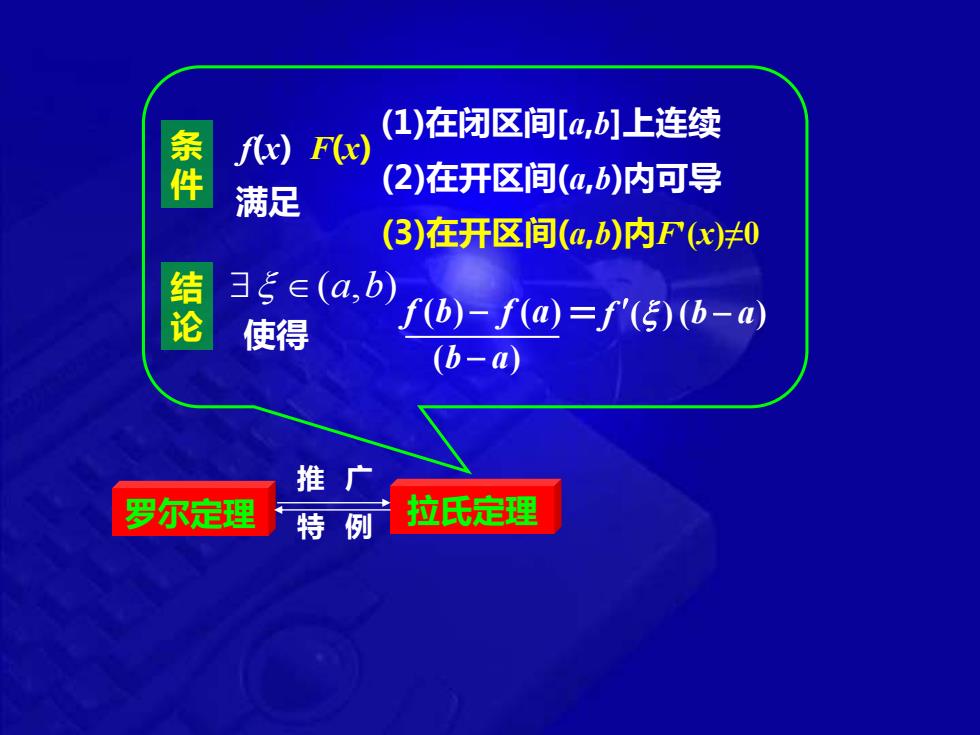
(1)在闭区间[a,b]上连续 f(x)F(x) 件 满足 (2)在开区间(a,b)内可导 (3)在开区间(a,b)内Fx)≠0 结 35∈(a,b) 使得 f(b)-f(a)=f'(5)(b-a) (b-a) 推广 罗尔定理 特 例 拉氏定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 f b f a ( ) ( ) − = f ( ) ( ) b a − 满足 条 件 结 论 罗尔定理 推 广 特 例 ( ) b a − F(x) (3)在开区间(a,b)内F'(x)≠0
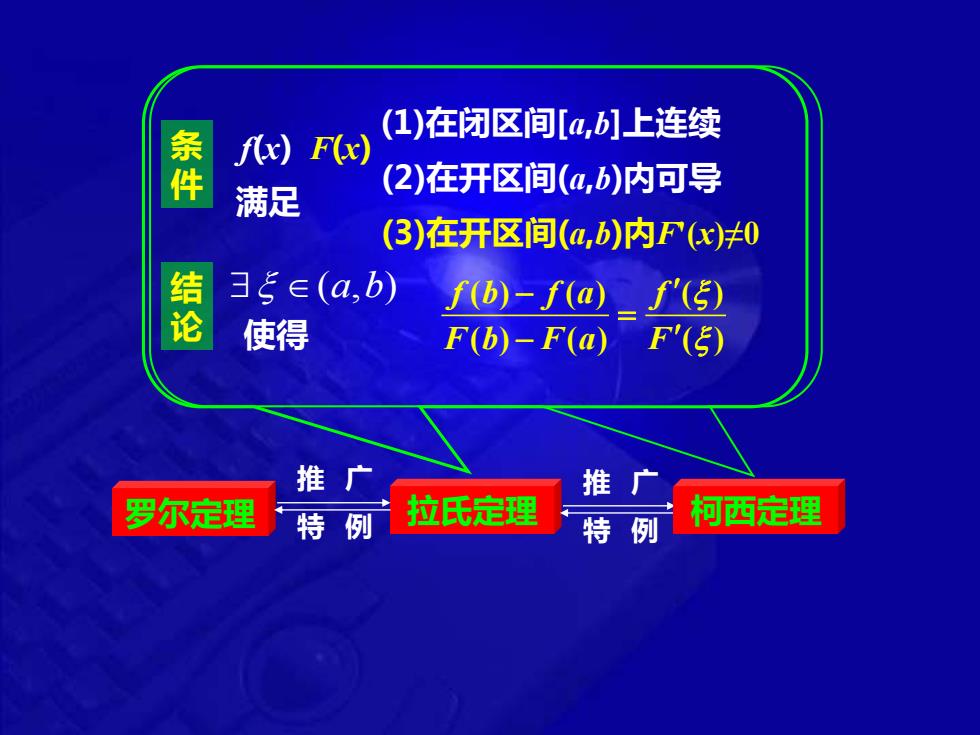
(1)在闭区间[a,b]上连续 fx)F(x) 件 (2)在开区间(a,b)内可导 满足 (3)在开区间(a,b)内Fx)≠0 35∈(a,b) f(b)-f(@)f(5) 论 使得 F(b)-F(a)F'(5) 推广 推 广 罗尔定理 特 例 拉氏定理 特 例 河西定理
拉氏定理 f(x) (1)在闭区间[a,b]上连续 (2)在开区间(a,b)内可导 (a,b) 使得 ( ) ( ) ( ) ( ) ( ) ( ) f b f a f F b F a F − = − 满足 条 件 结 论 罗尔定理 推 广 特 例 F(x) (3)在开区间(a,b)内F'(x)≠0 推 广 特 例 柯西定理