
先进控制理论与控制工程 中圆记质大学自动化学院吴敏 School of Aut 能控性(Controllability)分析 定义:存在一个输入(),使x(t)从任意的初始状态出发,在有限时间内达 到原点,则(A,B)是能控的。 定理:下述条件是等价的。 ·(A,B)是能控的: rank [B AB A2B...An-1B]=n; 存在实数矩阵F,使A+BF具有任意指定的个对称于实轴的复数 特征根; ·对于任意的复数,有rank[I-AB]=n。 30 2021年9月13日
30 2021年9月13日 能控性 (Controllability) 分析 定义: 存在一个输入u(t),使x(t)从任意的初始状态出发,在有限时间内达 到原点,则 (A,B) 是能控的。 定理: 下述条件是等价的。 • (A,B) 是能控的; • rank [B AB A2B … An-1B] = n; • 存在实数矩阵F,使A+BF具有任意指定的n个对称于实轴的复数 特征根; • 对于任意的复数,有rank [I-A B] = n。 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 能观性(Observability)分析 定义:任意的初始状态,可以由有限时间内的输出y(t)和输入()来唯一决 定,则(C,A)是能观的。 定理:下述条件是等价的。 (C,A)是能观的: rank [C CA CA2 ..CAnI]T=n; 存在实数矩阵H,使A+HC具有任意指定的n个对称于实轴的复 数特征根; ● 对于任意的复数,有rank[-ACT=n。 31 2021年9月13日
31 2021年9月13日 能观性 (Observability) 分析 定义: 任意的初始状态,可以由有限时间内的输出y(t)和输入u(t)来唯一决 定,则 (C,A) 是能观的。 定理: 下述条件是等价的。 • (C,A) 是能观的; • rank [C CA CA2 … CAn-1 ] T = n; • 存在实数矩阵H,使A+HC具有任意指定的n个对称于实轴的复 数特征根; • 对于任意的复数,有rank [I-A C] T = n。 先进控制理论与控制工程 吴 敏
先进控制理论与控制工程 中国地质大学自动化学院吴敏 内部稳定性分析 外部稳定性:输入输出(BIBO)稳定性,基于G(s)进行分析 内部稳定性:内部状态的收敛性,基于系统矩阵A进行分析 (A的特征根具有负实部) =Ax+Bu G(s)=C(sI-A)B+D y=Cx+Du 能控性+能观性:内部稳定性=外部稳定性 32 2021年9月13日
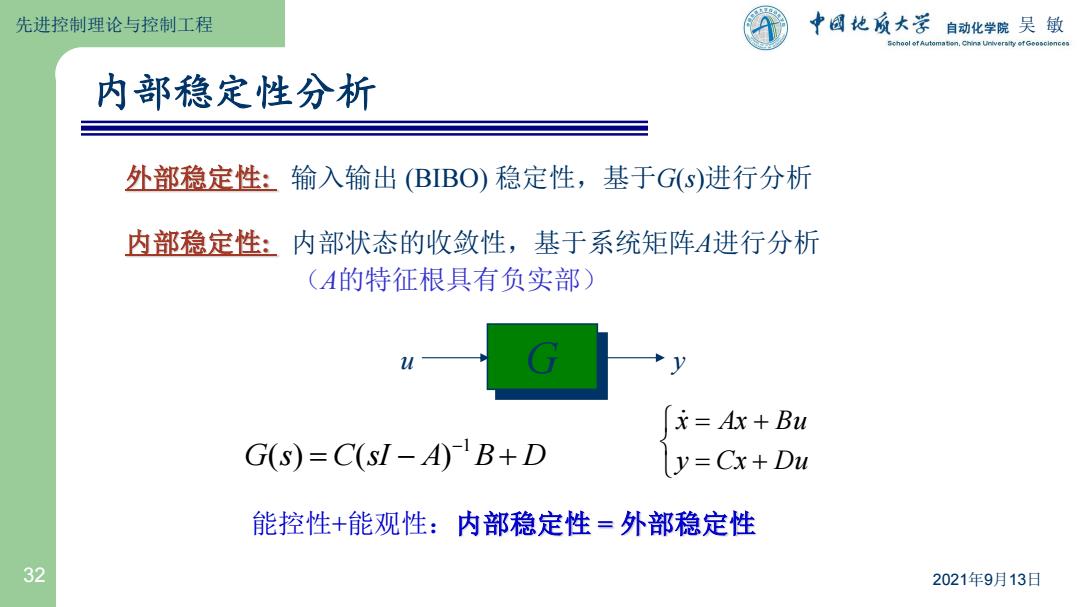
32 2021年9月13日 内部稳定性分析 外部稳定性: 输入输出 (BIBO) 稳定性,基于G(s)进行分析 内部稳定性: 内部状态的收敛性,基于系统矩阵A进行分析 (A的特征根具有负实部) u G y y Cx Du x Ax Bu G s C sI - A B D -1 ( ) ( ) 能控性+能观性:内部稳定性 = 外部稳定性 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中圆记质大学自动化学院吴敏 School of Aut LQ(Linear Quadratic)最优控制 LQ控制的基本特征: ·控制对象是线性的 ·控制目标是使线性二次型性能指标为最小 LQR问题:对于控制对象:x(t)=Ax(t)+Bu(t) 寻找控制规律:u(t)=-Kx(t) J=rOr+t'dRh 控制精度 控制能量(成本) 控制系统设计:寻找控制规律(①),实现minJ 控制问题的解:K=RBP(P为Riccati方程的解) 33 2021年9月13日
33 2021年9月13日 LQ (Linear Quadratic) 最优控制 LQ控制的基本特征: 控制系统设计:寻找控制规律u(t),实现min J x (t) Ax(t) Bu(t) 寻找控制规律: 对于控制对象: u(t) -Kx(t) LQR问题: J x t Qx t u t Ru t dt T T 0 ( ) ( ) ( ) ( ) 控制精度 控制能量 (成本) K R B P -1 T 控制问题的解: (P为Riccati方程的解) • 控制对象是线性的 • 控制目标是使线性二次型性能指标为最小 先进控制理论与控制工程 吴 敏

先进控制理论与控制工程 中国地质大学自动化学院吴敏 LQG(Linear Quadratic Gaussian)方法 LQG问题:对于控制对象:(t)=Ax(t)+B(t)+5 测量含有噪声:y=Cx+d E5(05'(x)】=E6t-t) 和u满足:k0dr(e=o6-t) 构造一个补偿器,产生一个控制输入,使如下性能指标最小: J=lim Ex"(t)Qx(t)+u"(t)Ru(t) 34 2021年9月13日
34 2021年9月13日 LQG (Linear Quadratic Gaussian) 方法 LQG问题: x (t) Ax(t) Bu(t) J lim Ex (t)Qx(t) u (t)Ru(t) T T t 测量含有噪声: 对于控制对象: 构造一个补偿器,产生一个控制输入u,使如下性能指标最小: y Cx d - - ( ) ( ) ( ) ( ) ( ) ( ) E d t d t E t t T T 和d满足: P y u d z 先进控制理论与控制工程 吴 敏