
Some special types of matrix Some special types of matrix zero matrix:a matrix,every element of which is zero. Note:Zero matrices of different orders are different. square matrix:as the name suggests,has the same number of rows as columns. 奇老这头子 Matrix Theory Matrices -3/14
Some special types of matrix Some special types of matrix ▸ zero matrix: a matrix, every element of which is zero. Note: Zero matrices of different orders are different. ▸ square matrix: as the name suggests, has the same number of rows as columns. ▸ row matrix (or vector): a 1 × m matrix, i.e., y ∈ C 1×m. ( 1 0 −1 2 ) ▸ column matrix (or vector): an n × 1 matrix, i.e., x ∈ C n×1 or shorter, x ∈ C n . ⎛ ⎜ ⎝ 6 4 3 ⎞ ⎟ ⎠ Matrix Theory Matrices - 3/14

Some special types of matrix Some special types of matrix zero matrix:a matrix,every element of which is zero. Note:Zero matrices of different orders are different. square matrix:as the name suggests,has the same number of rows as columns. row matrix (or vector):a 1 x m matrix,i.e.,ye Clxm. (10-12) 命电有这女子 Matrix Theory Matrices -3/14
Some special types of matrix Some special types of matrix ▸ zero matrix: a matrix, every element of which is zero. Note: Zero matrices of different orders are different. ▸ square matrix: as the name suggests, has the same number of rows as columns. ▸ row matrix (or vector): a 1 × m matrix, i.e., y ∈ C 1×m. ( 1 0 −1 2 ) ▸ column matrix (or vector): an n × 1 matrix, i.e., x ∈ C n×1 or shorter, x ∈ C n . ⎛ ⎜ ⎝ 6 4 3 ⎞ ⎟ ⎠ Matrix Theory Matrices - 3/14

Some special types of matrix Some special types of matrix zero matrix:a matrix,every element of which is zero. Note:Zero matrices of different orders are different. square matrix:as the name suggests,has the same number of rows as columns. row matrix(or vector)):小a1×m matrix,i.e,y∈Clxm. (10-12) column matrix (or vector):an nx 1 matrix,i.e.,x eCnx1 or shorter,xeC. 6 4 3 命电有这女 Matrix Theory Matrices -3/14
Some special types of matrix Some special types of matrix ▸ zero matrix: a matrix, every element of which is zero. Note: Zero matrices of different orders are different. ▸ square matrix: as the name suggests, has the same number of rows as columns. ▸ row matrix (or vector): a 1 × m matrix, i.e., y ∈ C 1×m. ( 1 0 −1 2 ) ▸ column matrix (or vector): an n × 1 matrix, i.e., x ∈ C n×1 or shorter, x ∈ C n . ⎛ ⎜ ⎝ 6 4 3 ⎞ ⎟ ⎠ Matrix Theory Matrices - 3/14

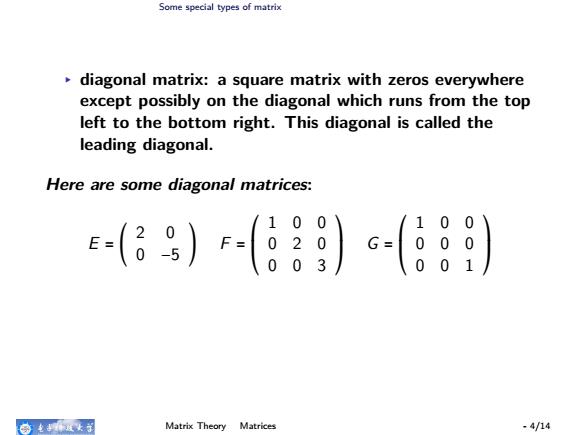
Some special types of matrix diagonal matrix:a square matrix with zeros everywhere except possibly on the diagonal which runs from the top left to the bottom right.This diagonal is called the leading diagonal. 命电有这女子 Matrix Theory Matrices -4/14
Some special types of matrix ▸ diagonal matrix: a square matrix with zeros everywhere except possibly on the diagonal which runs from the top left to the bottom right. This diagonal is called the leading diagonal. Here are some diagonal matrices: E = ( 2 0 0 −5 ) F = ⎛ ⎜ ⎝ 1 0 0 0 2 0 0 0 3 ⎞ ⎟ ⎠ G = ⎛ ⎜ ⎝ 1 0 0 0 0 0 0 0 1 ⎞ ⎟ ⎠ Note: Whereas all the non-diagonal elements are zero, the elements on the leading diagonal can be any number including zero. Matrix Theory Matrices - 4/14
Some special types of matrix diagonal matrix:a square matrix with zeros everywhere except possibly on the diagonal which runs from the top left to the bottom right.This diagonal is called the leading diagonal. Here are some diagonal matrices: 1 00 0 00 001 奇老有这头 Matrix Theory Matrices -4/14
Some special types of matrix ▸ diagonal matrix: a square matrix with zeros everywhere except possibly on the diagonal which runs from the top left to the bottom right. This diagonal is called the leading diagonal. Here are some diagonal matrices: E = ( 2 0 0 −5 ) F = ⎛ ⎜ ⎝ 1 0 0 0 2 0 0 0 3 ⎞ ⎟ ⎠ G = ⎛ ⎜ ⎝ 1 0 0 0 0 0 0 0 1 ⎞ ⎟ ⎠ Note: Whereas all the non-diagonal elements are zero, the elements on the leading diagonal can be any number including zero. Matrix Theory Matrices - 4/14