电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第七章 Bessel函数 §7.2 Bessel函数的母函数

§7.2 Besseli函数的母函数 一、】 esselE函数{Jn(x)} 的母函数 e-2() e产-2)- )] ■1730年左右，de Moivre用母函数来求解 Fabonaceis数列通项公式 1748年：Euler发展了母函数， 并用于解决分配问题 de Moivre 19世纪初，Laplace深入 研究 了母函数，并用于 处型概率同 PROBLEMS IN Euler ANALYSIS

§7.2 Bessel函数的母函数 2 一、Bessel函数 的母函数 2 0 1 ! 2 x k z k k x e z k           1 2 0 1 ( ) ! 2 x l z l l x e z l               1 ( ) 2 0 0 1 1 ( ) ! 2 ! 2 x k l z z k l k l x x e z z k l                                       J x n ( )

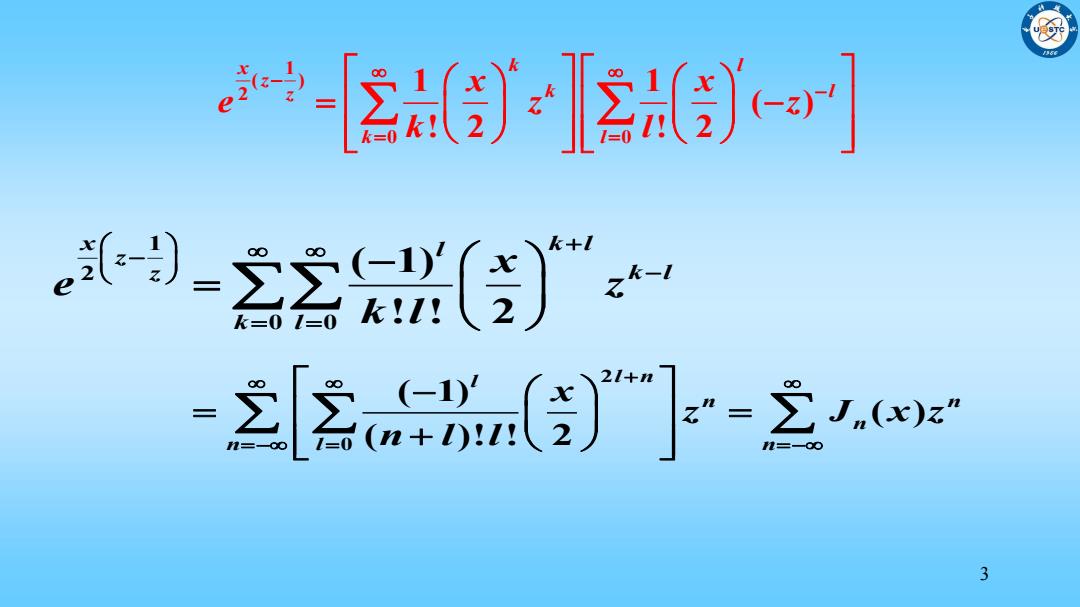
-2-引 9-22( k+ 2k-1 k三0 三房(g-空ws 3

3 1 ( ) 2 0 0 1 1 ( ) ! 2 ! 2 x k l z z k l k l x x e z z k l                                       1 2 0 0 ( 1) ! ! 2 x k l l z z k l k l x e z k l                        2 0 ( 1) ( ) ( )! ! 2 l l n n n n n l n x z J x z n l l                            

BesselE函数的母函数 w(e)=e(-) 令z=jeie ekomo-cos(xcos)+jsin(xcose)=)i"em -J(x)+>[J(x)j"eim+J()j-"e-wo] =J(x)+2>j"J(x)cosne 4

4 Bessel函数的母函数 令 j z ej   j cos j cos( cos ) jsin( cos ) ( )j x n n n n e x x J x e           1 2 ( ) x z z w z e         0 1 ( ) 2 j ( )cos n n n J x J x n      j j 0 1 ( ) ( )j ( )j n n n n n n n J x J x e J x e              

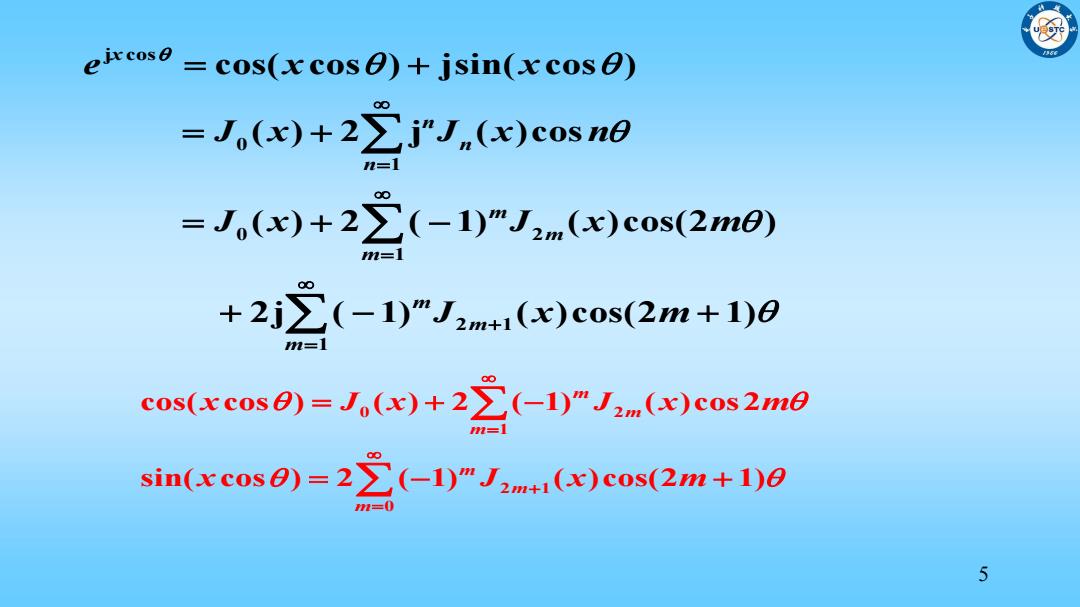
eixcoso cos(xcose)+jsin(xcose) =J(x)+2>j"J(x)cosne = =J(x)+2∑(-1)"J2m(x)cos(2m0) =1 +2j∑(-1)"J2m+1(x)c0s(2m+1)8 cos(xcos0)=J(x)+2>(-1)"J2m(x)cos2m0 I- sin(xcose)=2>(-1)"J2m(x)cos(2m+1)0 =0 5

5 j cos 0 1 0 2 1 2 1 1 cos( cos ) jsin( cos ) ( ) 2 j ( )cos ( ) 2 ( 1) ( )cos(2 ) 2j ( 1) ( )cos(2 1) x n n n m m m m m m e x x J x J x n J x J x m J x m                           0 2 1 2 1 0 cos( cos ) ( ) 2 ( 1) ( )cos2 sin( cos ) 2 ( 1) ( )cos(2 1) m m m m m m x J x J x m x J x m                 

二、Bessel函数的积分表达式 Laurent展式的系数公式 1=-o Laurent展式的系数公式 w=2j∮eae 取C为单位圆 6

6 二、Bessel函数的积分表达式 Laurent展式的系数公式 1 2 1 1 1 ( ) d 2 j x z z n C n J x e z  z           取C为单位圆 Laurent展式的系数公式 1 0 1 ( ) d 2πj ( ) n n C f z C z z z     1 ( ) 2 ( ) x z z n n n n n n e C z J x z         