电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第七章 Bessel函数 §7.1 Bessel方程的求解

激学物理方程与特殊函激精品课程 第七章Bessel函数 主讲：李明奇副教授

主讲：李明奇 副教授 第七章 Bessel函数

§7.1 Bessel方程的求解 一、n阶Bessel方程 x2 d'y 贝塞尔函数 岁+x%+(x2-n2)y=0 Bessel Functions n为任意实数和复数 不妨暂先假定心≥0，设方程有一个级数解形式为 y=x‘(a0+41x+a2x2+…akxk+…) =∑4kx+,an≠0 FRANK BOWMAN INTRODUCTION TO k=0 BESSEL FUNCTIONS 80 FRIEDRICH WILHELM BESSEL 1846

§7.1 Bessel方程的求解 2 一、n 阶Bessel方程 2 2 2 2 2 ( ) 0 d y dy x x x n y dx dx     n为任意实数和复数 不妨暂先假定 n≥0, 设方程有一个级数解形式为 2 0 1 2 0 0 ( ) , 0 c k k c k k k y x a a x a x a x a x a           

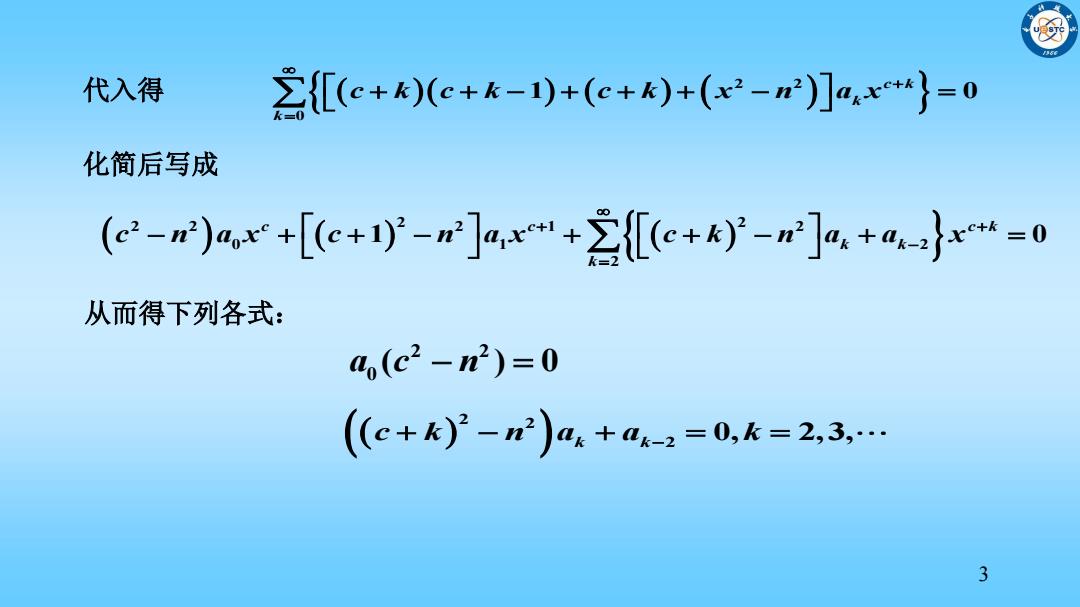
代入得 2{[(c+k)(e+k-)+(e+k)+(x2-)]ax}=0 化简后写成 (e2-r)a+[e+-]a,x+2e+k-n],+a}=0 从而得下列各式： a,(c2-2)=0 (c+k)-n2)0+ak-2=0,k=2,3,… 3

3 代入得          2 2 0 1 0 c k k k c k c k c k x n a x                 化简后写成         2 2 2 2 2 1 2 0 1 2 2 1 0 c c c k k k k c n a x c n a x c k n a a x                        从而得下列各式： 2 2 0 a c n ( ) 0      2 2 2 0, 2,3, k k c k n a a k      

取c=n 41=43=45=02=…=0 一Lk-2 ax=k(2n+k) -0 ao %=2(2n+2),0,=2-42n+2)(2n+4’ 一o a6=2.4:6(2n+2)(2n+4)(2n+6) a2m=(-10” do 2.4.6…2m(2n+2)(2n+4)…(2n+2m) 4

4 取 c=n 2 (2 ) k k a a k n k     1 3 5 7 a a a a      0 0 0 2 4 0 6 0 2 , , 2(2 2) 2 4(2 2)(2 4) 2 4 6(2 2)(2 4)(2 6) ( 1) 2 4 6 2 (2 2)(2 4) (2 2 ) m m a a a a n n n a a n n n a a m n n n m                     

a2m三 (-1)"a0 22mm:(n+1)(n+2)…(n+n) 一般项为 do xn+2m 22mm!(n+1)(n+2)…(n+n) (n+m)(n+n-1).(n+2)(n+1)T(n+1)=T(n+m+1) 1 1 ao=2"T(n+1) a2m=(-1)" 2n+2mm!Γ(n+m+1) y=之(-1)” +2m i=0 2+2"m!T(n+m+1) ,h≥0 5

5 0 2 2 ( 1) 2 !( 1)( 2) ( ) m m m a a m n n n m      一般项为 0 2 2 ( 1) 2 !( 1)( 2) ( ) m n m m a x m n n n m      ( )( 1) ( 2)( 1) ( 1) ( 1) n m n m n n n n m            2 2 1 ( 1) 2 ! ( 1) m m n m a  m n m      2 1 2 0 ( 1) , 0 2 ! ( 1) n m m n m m x y n m n m            0 1 2 ( 1) n a n   