电子科技大学：《数学物理方程与特殊函数 Mathematical Physics Equations with Special Function》课程教学资源（课件讲稿）第七章 Bessel函数 §7.4 Bessel函数应用

§7.4 Besselp函数应用 例设有半径为的薄圆盘，其侧面绝热，若圆盘边界上的温度恒保持为零度，且初 始温度为已知。求圆盘内的瞬时温度分布规律。 解： 2+ +R u(x,y,0)=p(x,y) u(x,y,t)=V(x,y)T(t) e+-R=0 Al址Bai约 Generalized T'=a2(VT+VnT） Bessel Functions of the First Kind V(c,y)+-gT0=0 u(x,y,0)=o(x,y)=p(pcose,psine)=f(p,0)

§7.4 Bessel函数应用 2 例 设有半径R为的薄圆盘，其侧面绝热，若圆盘边界上的温度恒保持为零度，且初 始温度为已知。求圆盘内的瞬时温度分布规律。 u x y t V x y T t ( , , ) ( , ) ( )  解：   2 2 2 2 2 2 2 2 2 2 2 , ( , ,0) , 0 x y R u u u a x y R t x y u x y x y u                                2 2 2 2 ( , ) ( ) 0 ( , ,0) ( , ) ( cos , sin ) ( , ) xx yy x y R VT a V T V T V x y T t u x y x y f                        

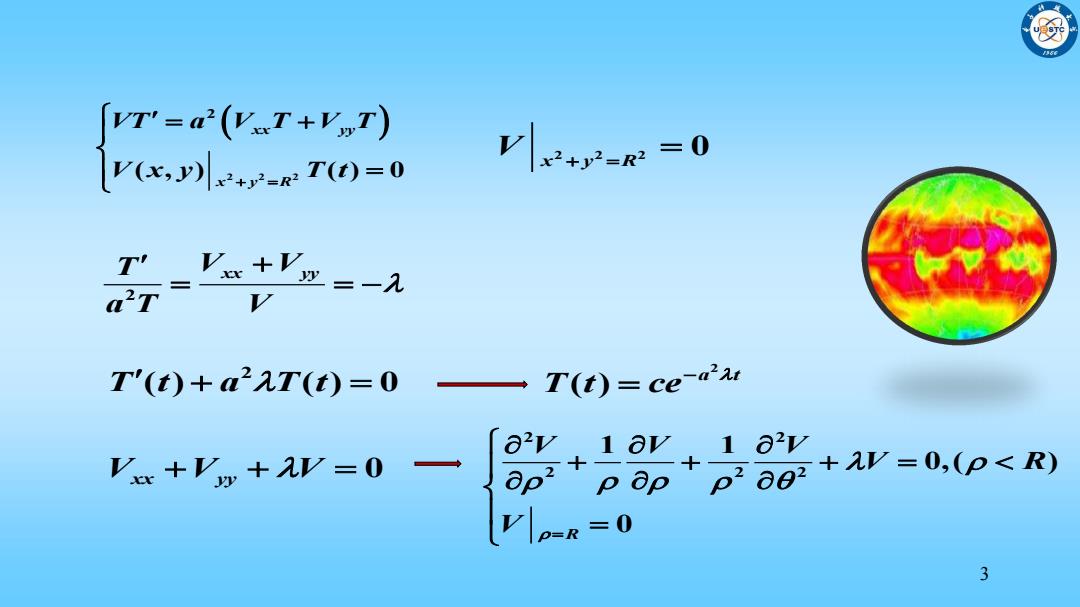
o V+-R=0 T'(t)+a2孔T(t)=0一 T(t)=ce-aa Vi +V+=0 +1 +pa8+r=0,(p<R) V=R=0 3

3 2 T V V xx yy a T V         2 2 2 2 ( , ) ( ) 0 xx yy x y R VT a V T V T V x y T t            2 T t a T t ( ) ( ) 0    2 2 2 0 x y R V    V V V xx yy     0 2 ( ) a t T t ce   2 2 2 2 2 1 1 0,( ) R 0 V V V V R V                         

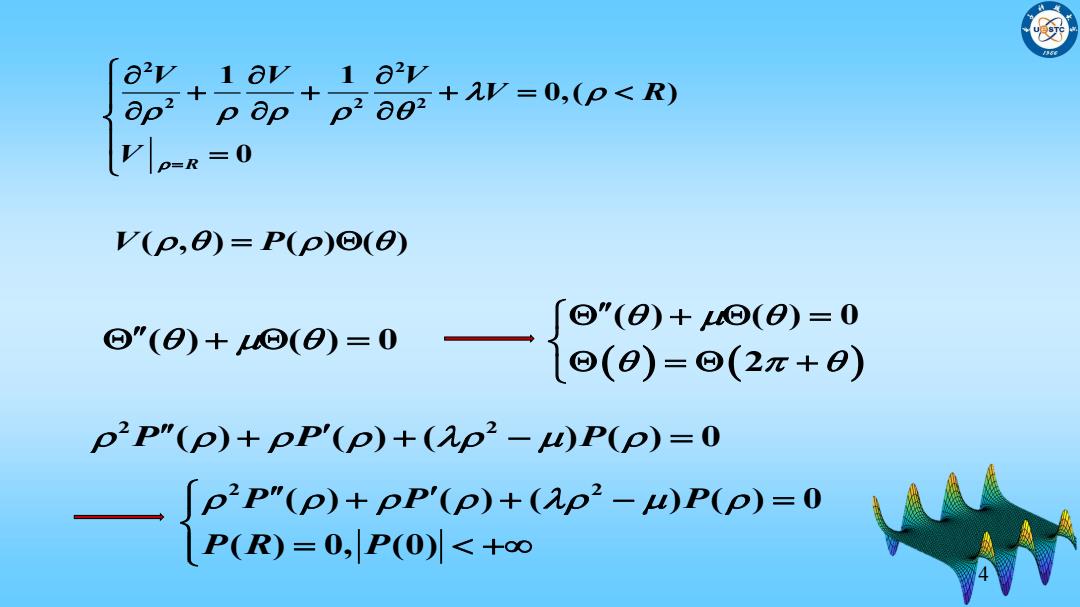
2/ E+P=0,(p<R) Ke-R=0 V(p,B)=P(p)⊙(B) oo+a0-0—8网89，l p2P"(p)+pP'(p)+(p2-)P(p)=0 —P6On-n-0

4 2 2 2 2 2 1 1 0,( ) R 0 V V V V R V                          V P ( , ) ( ) ( )           ( ) ( ) 0    2 2        P P P   ( ) ( ) ( ) ( ) 0         ( ) ( ) 0 2                  2 2 ( ) ( ) ( ) ( ) 0 ( ) 0, (0) P P P P R P                   

「⊙"(0)+⊙(0)=0 l⊙(0)=⊙(2x+8) hn=n2,n∈N ⊙，(0-2（为常数） 2 ()=a cosne+b'sin ne,n=1,2,... 5

5     ( ) ( ) 0 2                  2 , n   n n N 0 0 ( ) ( ) 2 ( ) cos sin , 1,2, n n n a a n b n n             为常数

RoR6n-o1-0 r=√夙p r2P"(r)+rP'(r)+(r2-n2)P( =0 P(r)=AJ (r)+BY (r) P(P)=AJ(Ap)+BY(Ap) Bessel Runctiors of the Rirst Kind 3. 0 limy (x)=-oo B=0 x→0 05

6 r    2 2 2 r P r rP r r n P r   ( ) ( ) ( ) ( ) 0     2 2 2 ( ) ( ) ( ) ( ) 0 ( ) 0, (0) P P n P P R P                   ( ) ( ) ( ) P r AJ r BY r   n n ( ) ( ) ( ) P AJ BY        n n 0 lim ( ) n x Y x    B  0