
3)、电容元件的s域模型 wf, =∫.(nr 0) +v(t) 1 10) s)=s)+3 +vc(0) 1) 's) 内电源极性与电容两端极性一致 电流源形式: 1c) sC Ic(s)=sCVc(s)-Cvc(0_) C0) ① Vc(s)
(3)、电容元件的s域模型 11 (0 ) 1 1 ( ) ( ) C = C + C − v sC s V s I s 电流源形式: sC 1 ( ) − 0 1 C v s I (s) C + V (s) − C I (s) C sC 1 ( ) CvC 0− + V (s) C − ( ) ( ) − = t C C i t C v t d 1 ( ) ( ) (0 ) C = C −CvC − I s sCV s i c (t) c + v (t) - c (0 ) − c v 内电源极性与电容两端极性一致

12 注意: 1.内电压源极性只与电容两端电压有关; 内电流源方向只与电感电流有关; 2.“等效”概念(端子); 3.1>-,6(t)>1 GC心g0o外恕G包卷M@3入9海
12 1. 内电压源极性只与电容两端电压有关; 内电流源方向只与电感电流有关; 2. “等效”概念(端子); , (t) 1 s 1 3.1 注意:

复频域电路模型:将原电路中已知电压源和电流源都变 换为相应的拉氏变换;未知电压、电流也用其拉氏变换 表示;各电路元件都用其复频域模型代替(初始状态变 换为相应的电源)。 对该电路模型而言,用以分析计算正弦稳态电路的 各种方法((如无源支路的串、并联、电压源与电流源 的等效变换等等)都适用。无需列写电路的微分方程。 i()分I(),KCL:∑i0)=0→∑Is)=0 v(t)分V(s)KVL:∑)=0→∑V(s)=0
13 复频域电路模型: 将原电路中已知电压源和电流源都变 换为相应的拉氏变换;未知电压、电流也用其拉氏变换 表示;各电路元件都用其复频域模型代替(初始状态变 换为相应的电源)。 对该电路模型而言,用以分析计算正弦稳态电路的 各种方法(如无源支路的串、并联、电压源与电流源 的等效变换等等)都适用。无需列写电路的微分方程。 i(t) I(s), v(t) V(s) KCL :i(t) = 0 → I(s) = 0 KVL :v(t) = 0 → V(s) = 0

14 用电的蚧域僕塑型棒逑博型蝶替(初 始状态转换为相应的内电源); 2.信号源及各变量用其拉氏变换式代替; 3.画出电路的复频域模型; 4应用电路分析的各种方法和定理求解响应的变 换式。 5.反变换得响应的时域表达式
用电路的复频域模型求解响应的步骤 14 1. 电路中的每个元件都用其复频域模型代替(初 始状态转换为相应的内电源); 2. 信号源及各变量用其拉氏变换式代替; 3. 画出电路的复频域模型; 4. 应用电路分析的各种方法和定理求解响应的变 换式。 5. 反变换得响应的时域表达式
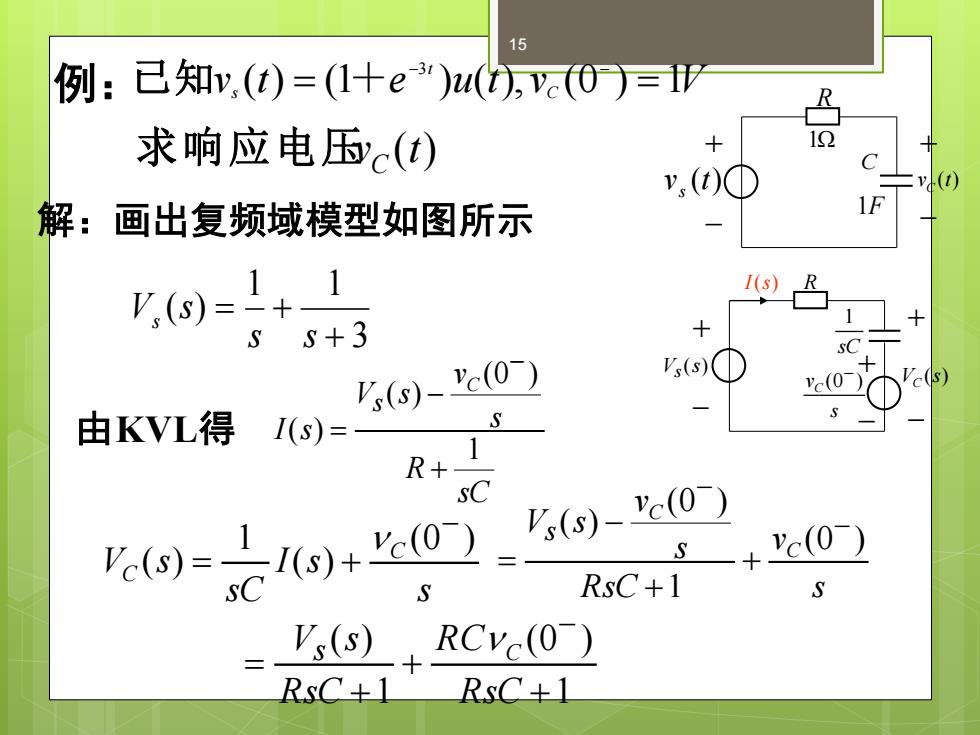
例:已知v,(t)=(1+e')(,0)= R 求响应电压(t) v,()① 解:画出复频域模型如图所示 )=1+1 I(s) R ss+3 (s)-"e(0) 'c(0 由KVL得I(s)= S ()=1)+0)_ (s)-(0) 'c(0) S RsC+1 V、(s),RCyc(0) RsC+1 RsC+1
15 v t e u t vC V t s ( ) (1 ) ( ), (0 ) 1 3 = = 已 知 + − − v (t) 求响应电压 C 3 1 1 ( ) + = + s s V s s sC R s v V s I s C s 1 (0 ) ( ) ( ) + − = − 解:画出复频域模型如图所示 v (t) s R C 1 1F v (t) C + + − − V (s) s V (s) C + + − − + − s vC (0 ) − sC 1 I(s) R 由KVL得 s I s sC V s C C (0 ) ( ) 1 ( ) − = + s v RsC s v V s C C s (0 ) 1 (0 ) ( ) − − + + − = 1 (0 ) 1 ( ) + + + = − RsC R C RsC V s s C 例: