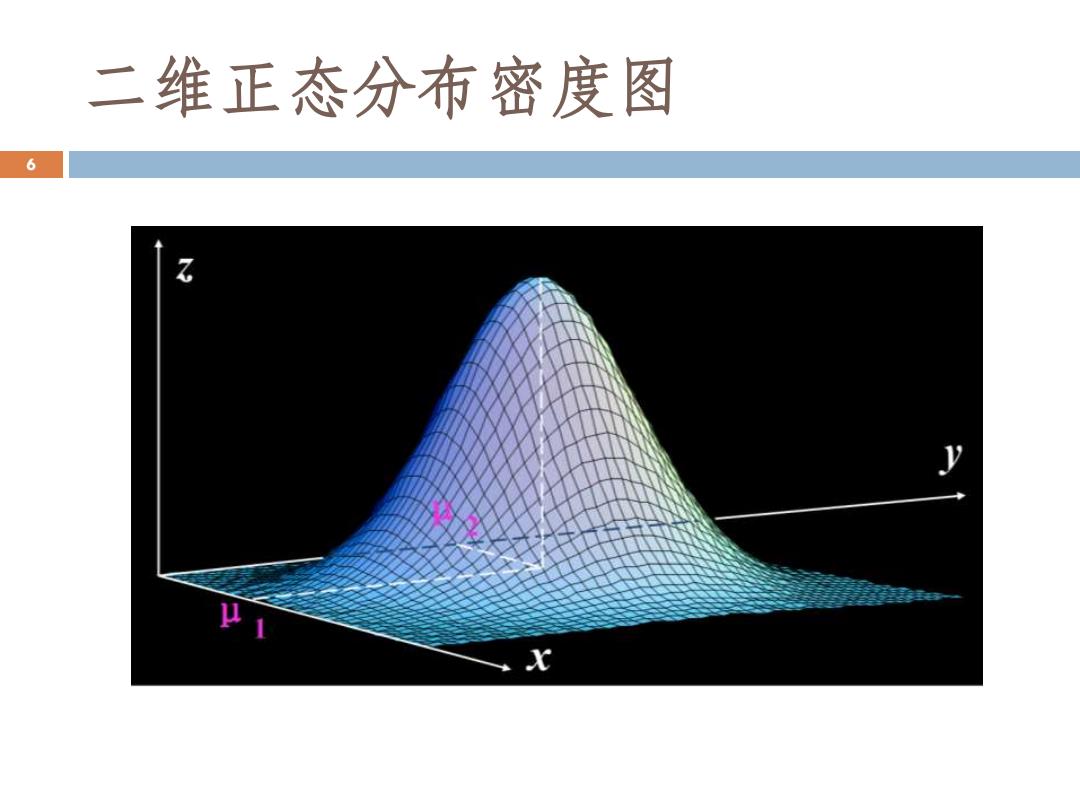
二维正态分布密度图 6 乙 y X
二维正态分布密度图 6

二维正态分布剖面图 7
二维正态分布剖面图 7

二维正态分布的边缘分布 8 口设(X,Y)~N(u1u2,oo2p),则 X~N(1,o),Y~N(2,o) 即:Px(x)= e 2元01 2a1,-00<X<十00 -2)2 pr(y)= 2mo2 2a吃,-00<y<+0 二维正态分布的边缘分布仍是正态分布 证:根据边缘分布的定义,换元积分即可
二维正态分布的边缘分布 设 𝑿, 𝒀 ∼ 𝑵 𝝁𝟏,𝝁𝟐,𝝈𝟏 𝟐 ,𝝈𝟐 𝟐 ,𝝆 ,则 𝑿 ∼ 𝑵 𝝁𝟏,𝝈𝟏 𝟐 ,𝒀 ∼ 𝑵 𝝁𝟐,𝝈𝟐 𝟐 即:𝒑𝑿 𝒙 = 𝟏 𝟐𝝅𝝈𝟏 𝒆 − 𝒙−𝝁𝟏 𝟐 𝟐𝝈𝟏 𝟐 , −∞ < 𝒙 < +∞ 𝒑𝒀 𝒚 = 𝟏 𝟐𝝅𝝈𝟐 𝒆 − 𝒚−𝝁𝟐 𝟐 𝟐𝝈𝟐 𝟐 , −∞ < 𝒚 < +∞ 8 二维正态分布的边缘分布仍是正态分布 证:根据边缘分布的定义,换元积分即可

二维正态随机变量的独立性 9 定理:设(X,Y)N(1,42,o1,吃,p),则 X,Y相互独立的充要条件为:p=0。 证明:p=0时,二维正态(X,)的密度函数: p(x,)= 2πo02V1-p ewp20'ply -2p(*4'二)+('-4)21]} ap,0gy]}
二维正态随机变量的独立性 9 定理:设 𝑿, 𝒀 ∼ 𝑵(𝝁𝟏,𝝁𝟐, 𝝈𝟏 𝟐 , 𝝈𝟐 𝟐 , 𝝆),则 𝑿, 𝒀相互独立的充要条件为:𝝆 = 𝟎