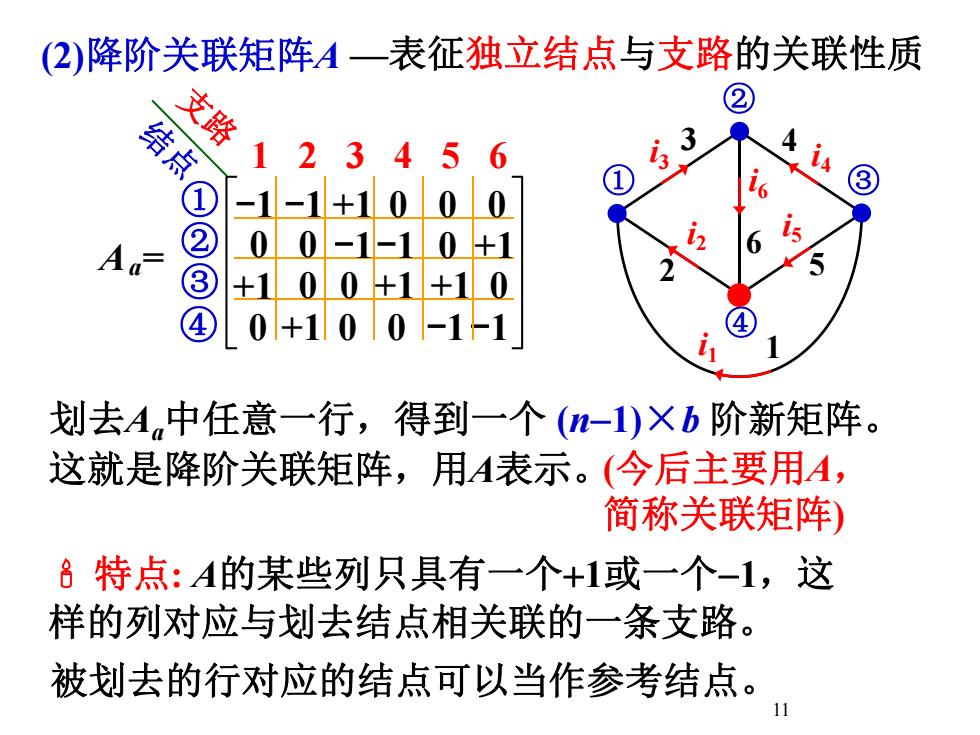
(2)降阶关联矩阵A一表征独立结点与支路的关联性质2支路结点264431101115i260520A划去A,中任意一行,得到一个(n-1)×b阶新矩阵这就是降阶关联矩阵,用A表示。(今后主要用A简称关联矩阵8特点:A的某些列只具有一个+1或一个-1,这样的列对应与划去结点相关联的一条支路。被划去的行对应的结点可以当作参考结点。11
11 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ (2)降阶关联矩阵A 划去Aa中任意一行,得到一个 (n-1)×b 阶新矩阵。 特点: A的某些列只具有一个1或一个-1,这 样的列对应与划去结点相关联的一条支路。 0 +1 0 0 -1 -1 A = ① ② ③ 1 2 3 4 5 6 -1 -1 +1 0 0 0 0 0 -1-1 0 +1 +1 0 0 +1 +1 0 支 结 路 点 a ④ 这就是降阶关联矩阵,用A表示。(今后主要用A, 简称关联矩阵) 被划去的行对应的结点可以当作参考结点。 —表征独立结点与支路的关联性质
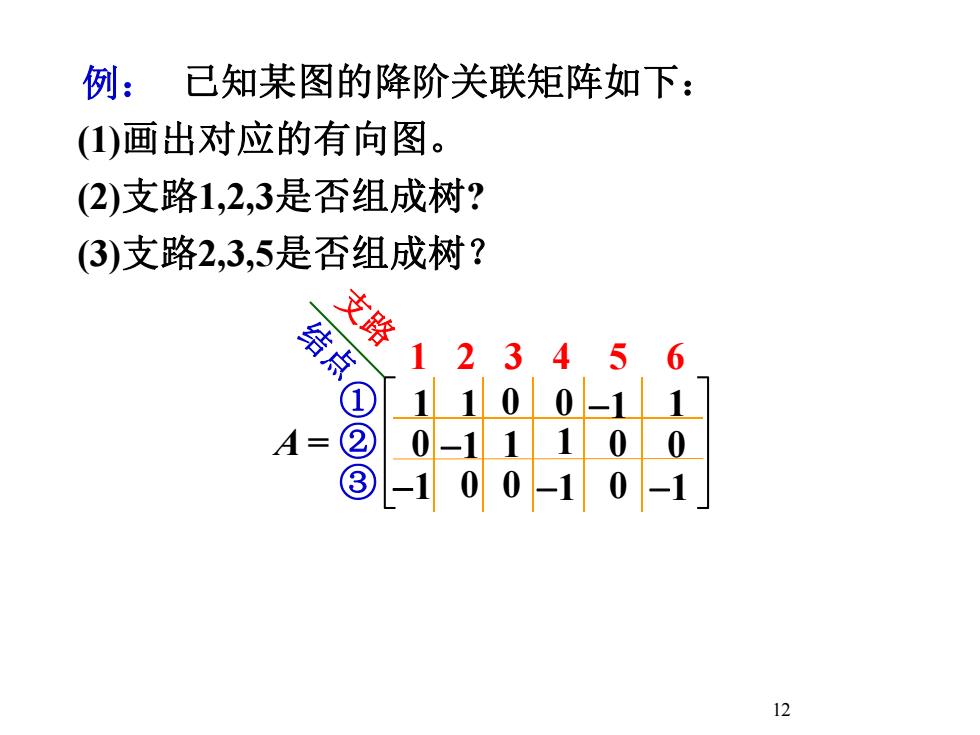
例:已知某图的降阶关联矩阵如下(1)画出对应的有向图。(2)支路1,2,3是否组成树?(3)支路2,3,5是否组成树?支路结点2+①②A=③012
例: 12 已知某图的降阶关联矩阵如下: (1)画出对应的有向图。 (2)支路1,2,3是否组成树? (3)支路2,3,5是否组成树? A = ① ② ③ 1 2 3 4 5 6 1 1 0 0 -1 1 支 结 路 点 0 -1 1 1 0 0 -1 0 0 -1 0 -1
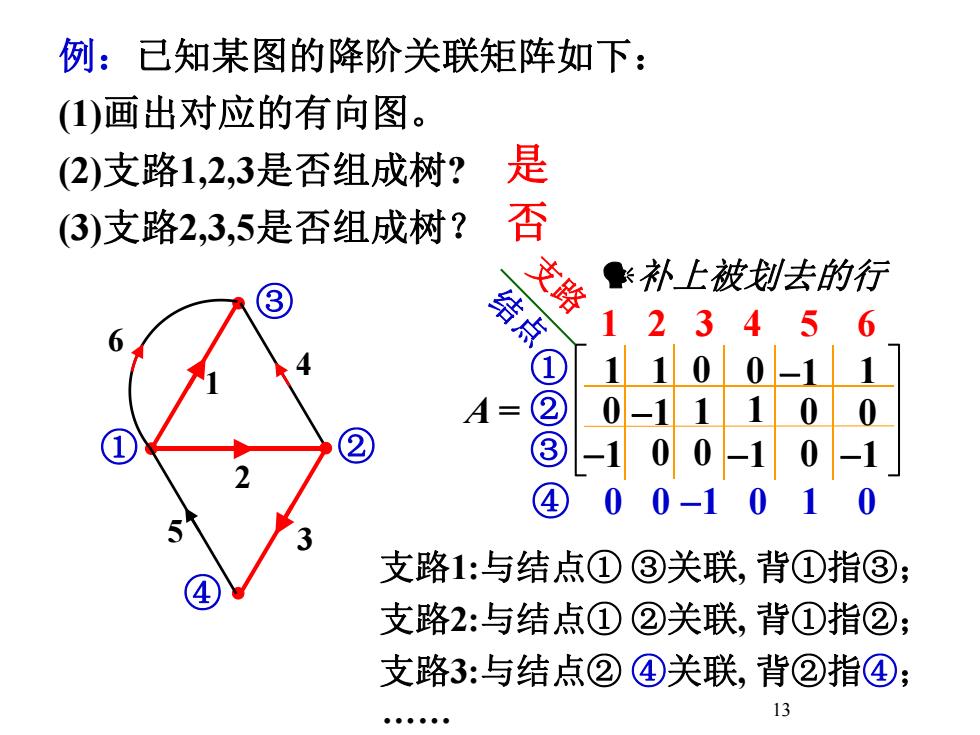
例:已知某图的降阶关联矩阵如下:(1)画出对应的有向图。是否(2)支路1,2,3是否组成树?(3)支路2,3,5是否组成树?支路补上被划去的行3结点234①2A=2③0401D3支路1:与结点①③关联,背①指③:支路2:与结点①②关联,背①指②:支路3:与结点②④关联,背②指④:13
13 例:已知某图的降阶关联矩阵如下: (1)画出对应的有向图。 (2)支路1,2,3是否组成树? (3)支路2,3,5是否组成树? ④ 0 0 -1 0 1 0 A = ① ② ③ 1 2 3 4 5 6 1 1 0 0 -1 1 支 结 路 点 0 -1 1 1 0 0 -1 0 0 -1 0 -1 支路1:与结点① ③关联, 背①指③; ① ③ ② ④ 支路2:与结点① ②关联, 背①指②; 支路3:与结点② ④关联, 背②指④; . 补上被划去的行 1 2 3 4 5 6 是 否
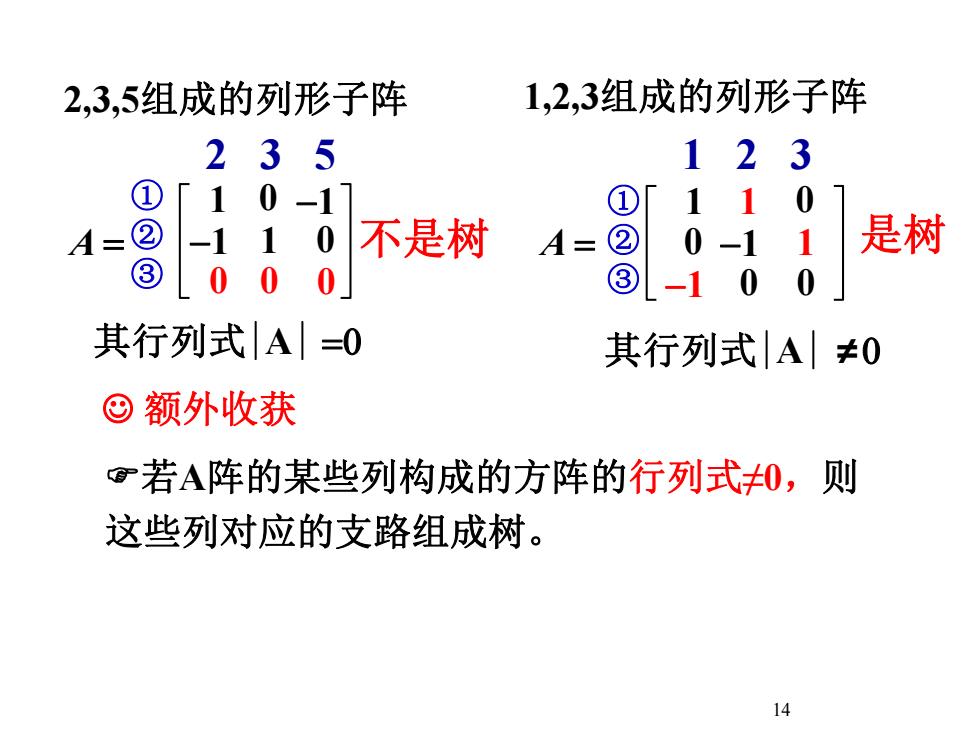
1,2,3组成的列形子阵2,3,5组成的列形子阵51323210 -1011是树不是树20A=②10 -1-113③00000-1其行列式|A|=0其行列式|A丨±0?额外收获则若A阵的某些列构成的方阵的行列式0,这些列对应的支路组成树。14
14 A 1 0 -1 -1 1 0 0 0 0 2 3 5 ① ② ③ A 1 1 0 0 -1 1 -1 0 0 1 2 3 ① ② ③ 2,3,5组成的列形子阵 1,2,3组成的列形子阵 其行列式|A| 0 额外收获 若A阵的某些列构成的方阵的行列式≠0,则 这些列对应的支路组成树。 不是树 是树 其行列式|A| ≠0
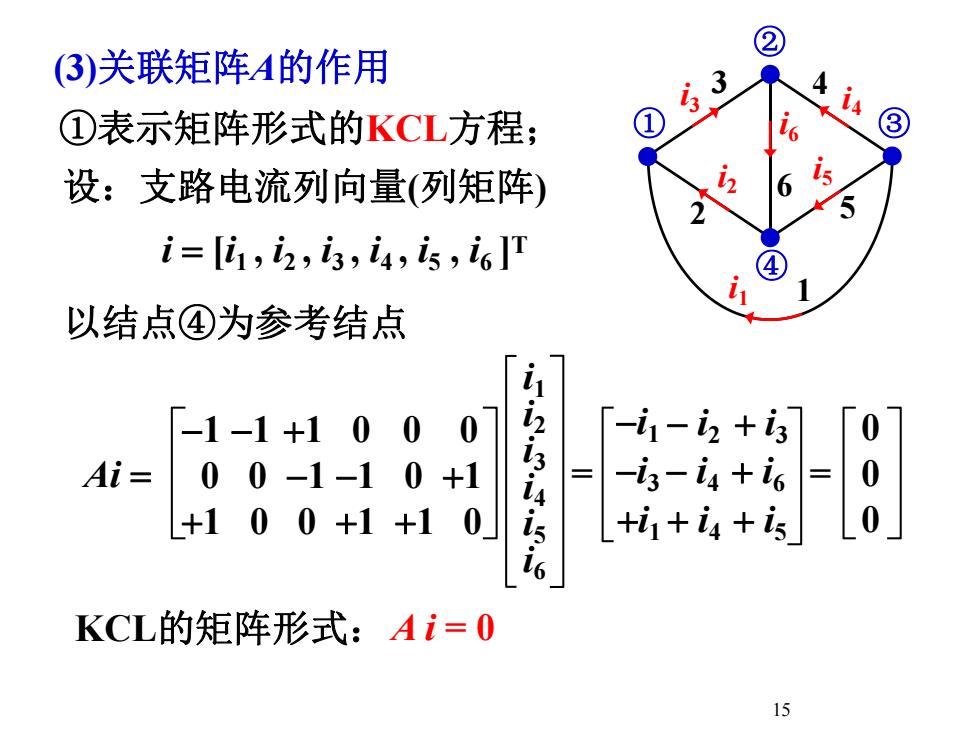
②(3)关联矩阵A的作用34is141ig3①表示矩阵形式的KCL方程isi26设:支路电流列向量(列矩阵52i=[i,, i,i4, is, i]T4L以结点④为参考结点i23i4i5.-i-iz +i0001+10-is-i +icAi==0+100110000+1+1+1+i+i +is6KCL的矩阵形式:Ai= 015
15 (3)关联矩阵A的作用 -1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 1 1 0 i1 i2 i3 i4 i5 i6 = -i1 -i3 - i4 i6 i1 i4 i5 = 0 0 0 A i = 0 ①表示矩阵形式的KCL方程; 以结点④为参考结点 - i2 i3 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ KCL的矩阵形式: i [i1 , i2 , i3 , i4 , i5 , i6 ]T 设:支路电流列向量(列矩阵) Ai