
*引言在第三章里,我们学习了图的基本知识和电路的基本分析方法,本章是在第三章的基础上,对电路进行更深入的讨论,即应用图论的知识研究电路方程的系统列写方法及方程的矩阵形式。本章的研究目的着眼于方法的系统化,以便于利用计算机作为工具进行辅助分析。所以,学习这一章的自的是为此作理论准备的6
6 引言 在第三章里,我们学习了图的基本知识和电路 的基本分析方法,本章是在第三章的基础上, 对电路进行更深入的讨论,即应用图论的知识, 研究电路方程的系统列写方法及方程的矩阵形 式。本章的研究目的着眼于方法的系统化,以 便于利用计算机作为工具进行辅助分析。所以, 学习这一章的目的是为此作理论准备的

$15-2割集矩阵关联矩阵、回路矩阵、售研究系统化建立方程的方法,且方程用矩阵形式表示。图的矩阵表示:指用矩阵描述图的拓扑性质即KCL和KVL的矩阵形式有三种矩阵形式:哪三种?结点—支路关联矩阵回路矩阵回路一支路割集矩阵割集一支路7
7 §15-2 关联矩阵、回路矩阵、割集矩阵 研究系统化建立方程的方法,且方程用矩阵 形式表示。 图的矩阵表示:指用矩阵描述图的拓扑性质, 即KCL和KVL的矩阵形式。 有三种矩阵形式: 结点 支路 关联矩阵 回路 支路 回路矩阵 割集 支路 割集矩阵 哪三种?

1.关联矩阵A描述结点与支路的关联性质n个结点b条支路的图用nxb的矩阵A,描述:支路b结点每一行对应一个结点,nxbA=每一列对应一条支路。n(1) 元素定义支路k与结点i关联,方向背离结点;+1支路k与结点i关联,方向指向结点:aik=支路k与结点i无关背离+1,指向-1,无关0。ajk:
1. 关联矩阵A ——描述结点与支路的关联性质 每一行对应一个结点, (1) 元素定义 ajk 1 支路 k 与结点 j 关联,方向背离结点; -1 支路 k 与结点 j 关联,方向指向结点; 0 支路 k 与结点 j 无关。 Aa = nb n个结点b条支路的图用 nb 的矩阵Aa描述: 结 点 n 支路b 每一列对应一条支路。 ajk:背离1,指向-1,无关0
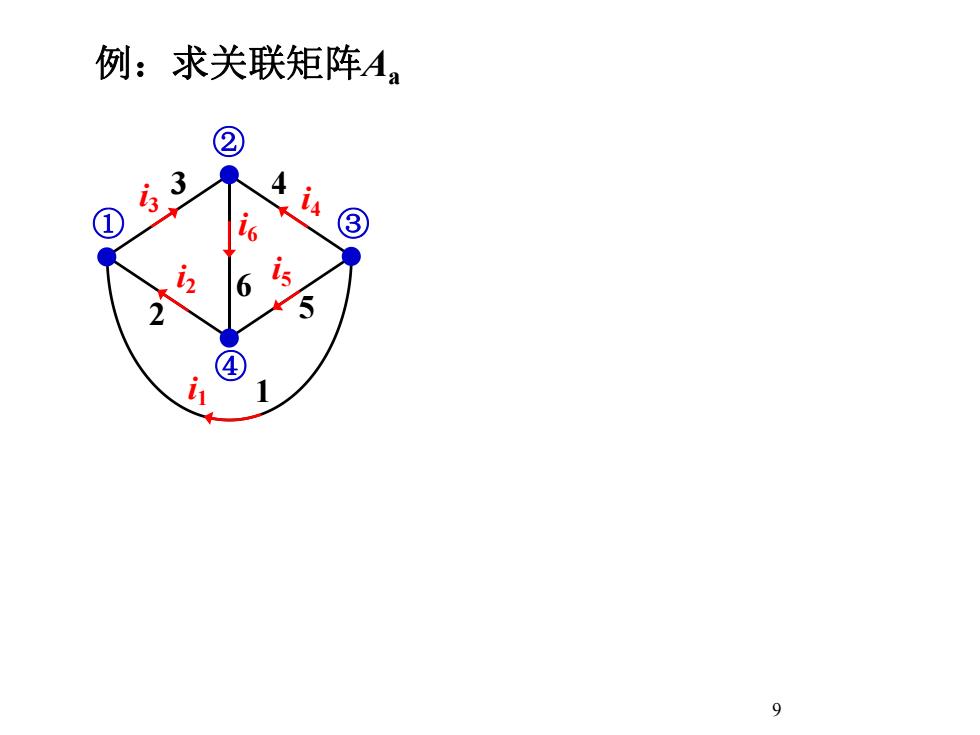
例:求关联矩阵A,233316isi2652A
9 例:求关联矩阵Aa i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④

背离+1,指向-1,无关0。ajk:2按行列写33支路3结点2345isi26①??52Aa4吕注意其特点①每一列只有两个非零元素,一个是+1,一个?是-1,A,的每一列元素之和为零;②矩阵中任一行可以从其他n-1行中导出,即只有n-1行是独立的。10
10 Aa = ① ② ③ ④ 1 2 3 4 5 6 -1 -1 +1 0 0 0 0 0 -1 -1 0 +1 +1 0 0 +1 +1 0 0 +1 0 0 -1 -1 ajk:背离1,指向-1,无关0。 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ 支 结 路 点 注意其特点 ②矩阵中任一行可以从其他 n-1行中导出,即 只有n-1行是独立的。 ? 按行 列写 ①每一列只有两个非零元素,一个是1,一个 是-1,Aa的每一列元素之和为零;