第10章含有耦合电感的电路UT本章目录互感10.1含有耦合电感电路的计算10.2耦合电感的功率10.3变压器原理10.4理趣变压器10.5传!
SDUT 内 部 资 料! 请 勿 外 传! 1 第10章 含有耦合电感的电路 本章目录 10.1 互感 10.2 含有耦合电感电路的计算 10.3 耦合电感的功率 10.4 变压器原理 10.5 理想变压器

8重点1.耦合电感的相关概念(互感、同名端等);2.耦合电感的伏安关系3.含有互感电路的计算(直接列方程法、去耦等效法、原边副边等效电路法)4.理想变压器的分析计算资料!丫难点1.耦合电感的同名端及互感电压极性的确定:2.含有耦合电感的电路的方程3.理想变压器电路的分析富本章与其它章节的联系本章的学习内容建立在前面各章理论的基础之上。2
SDUT 内 部 资 料! 请 勿 外 传! 2 难点 本章与其它章节的联系 本章的学习内容建立在前面各章理论的基础之上。 1. 耦合电感的相关概念(互感、同名端等); 2. 耦合电感的伏安关系 3.含有互感电路的计算(直接列方程法、去耦等效 法、原边副边等效电路法); 4. 理想变压器的分析计算。 1. 耦合电感的同名端及互感电压极性的确定; 2. 含有耦合电感的电路的方程; 3.理想变压器电路的分析
S 10-1互感1.耦合电感的相关概念一个线圈的情况i产生的磁通为u。dui与Φ的参考方向符合右手螺旋法则,为料0-关联的参考方向,uu十Φ,穿越自身线圈时,若uu与i取关联参考方向产生的自感磁通链用dYdi则uin,表示:=Lidtd请若u;非关联参考方向当i变化时,将产生自感电压ui。3
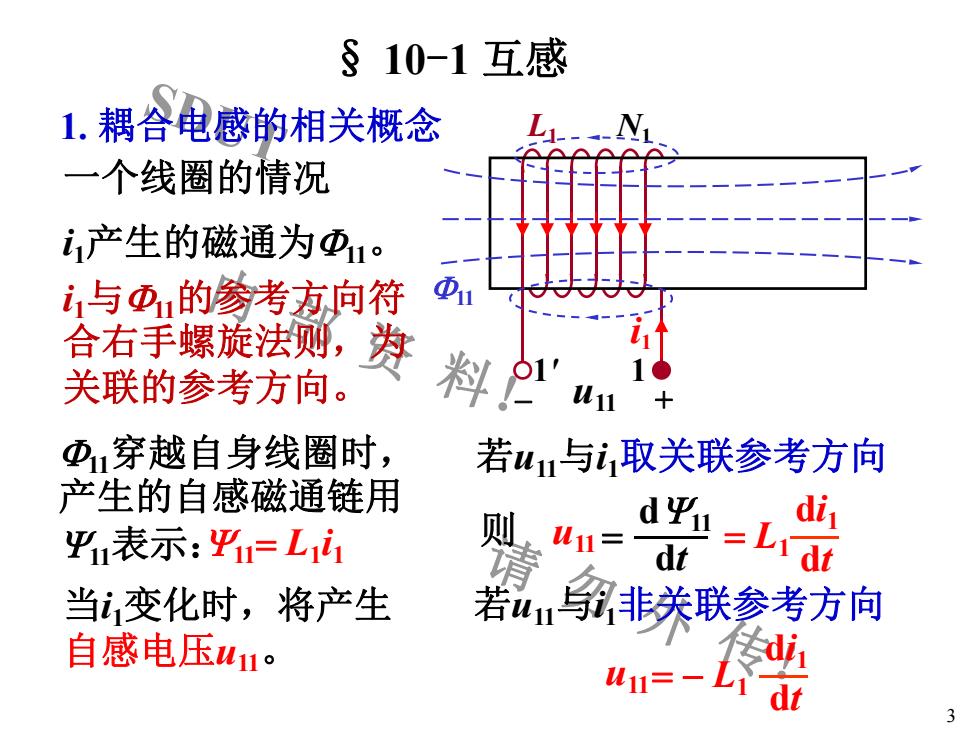
SDUT 内 部 资 料! 请 勿 外 传! 3 § 10-1 互感 1. 耦合电感的相关概念 L1 N1 1' 1 i1 F11 i1产生的磁通为F11。 i1与F11的参考方向符 合右手螺旋法则,为 关联的参考方向。 F11穿越自身线圈时, 产生的自感磁通链用 Y11表示:Y11= L1 i1 当i1变化时,将产生 自感电压u11。 - u11 + 若u11与i1取关联参考方向 则 u11= dt dY11 = L1 dt di1 若u11与i1非关联参考方向 u11= - L1 dt di1 一个线圈的情况
N2L2(1) 互感概念21则若L,邻近一线圈L,,Φu的一部分穿过L2°DP22内部22'001一→自感磁通du一→自感磁通链i通入i一→互感磁通—互感磁通链421施感电流—→自感磁通Φ22—→自感磁通链手422通入i一→互感磁通Φi2互感磁通链Y12载流线圈之间通过彼此的磁场相互联系的物理传!现象称为磁耦合,这就是互感现象。4
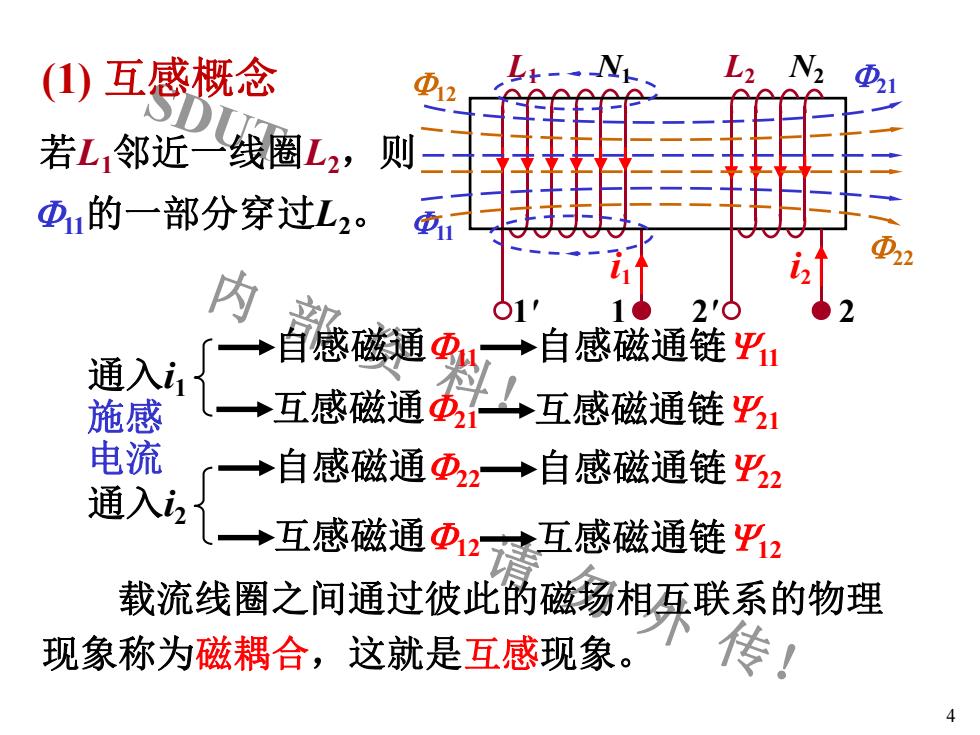
SDUT 内 部 资 料! 请 勿 外 传! (1) 互感概念 4 L1 N1 1' 1 i1 F11 L2 N2 2' 2 F11的一部分穿过L2。 F21 i2 F22 F12 通入i1 自感磁通F11 自感磁通链Y11 互感磁通F21 互感磁通链Y21 通入i2 自感磁通F22 自感磁通链Y22 互感磁通F12 互感磁通链Y12 施感 电流 载流线圈之间通过彼此的磁场相互联系的物理 现象称为磁耦合,这就是互感现象。 若L1邻近一线圈L2,则
d(2)互感系数M2两线圈都有电流时,每一线圈的磁链均为自磁链与互磁Ddp22链的代数和。222'0Y=Yi12 =L±M12i2+- uz+u2=Y22422i2±M21i资料!注意:①大小M值与线圈的形状、几何位置、空间媒质有关,与线圈中的电流无关,Miz=Ma1(从M的定义出发将面积分化为曲线积分证明);请勿M前正负2)+号:表示互磁链与自磁链方向一致,自感方向的磁场得到增强,称为同向耦合;否则为反尚耦合(-号)
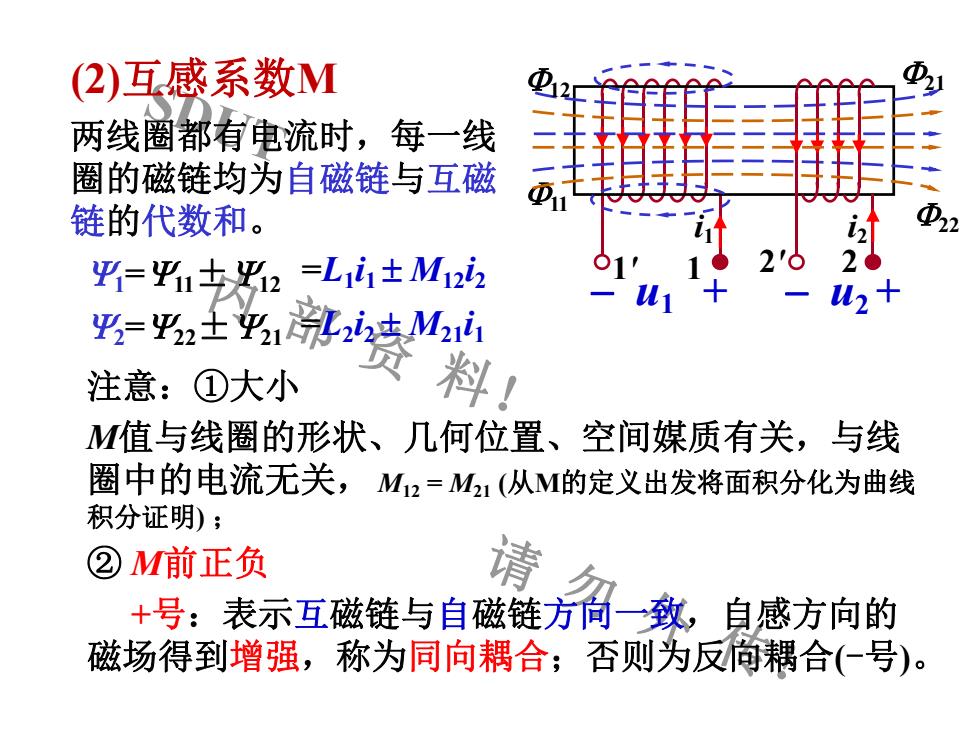
SDUT 内 部 资 料! 请 勿 外 传! - u1 + - u2 + (2)互感系数M 5 Y1=Y11±Y12 Y2=Y22±Y21 =L1 i1 M12 i2 =L2 i2 M21 i1 两线圈都有电流时,每一线 圈的磁链均为自磁链与互磁 链的代数和。 1' 1 F11 2' 2 F21 i2 F22 F12 注意:①大小 M值与线圈的形状、几何位置、空间媒质有关,与线 圈中的电流无关, M12 = M21 (从M的定义出发将面积分化为曲线 积分证明) ; ② M前正负 +号:表示互磁链与自磁链方向一致,自感方向的 磁场得到增强,称为同向耦合;否则为反向耦合(-号)。 i1