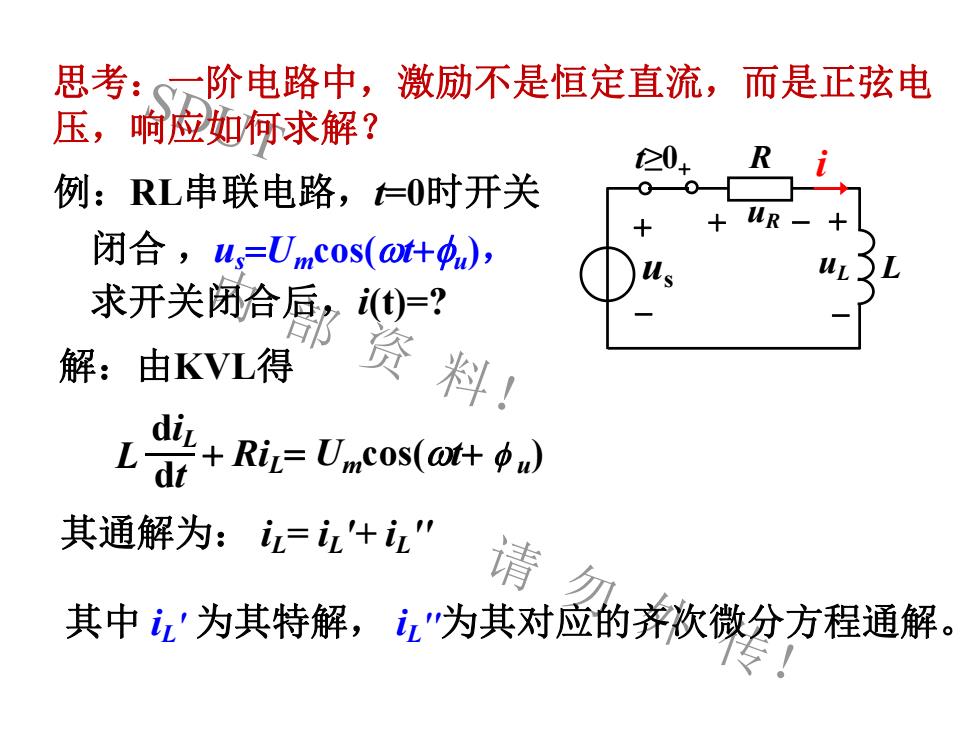
思考:一阶电路中,激励不是恒定直流,而是正弦电压,响应如何求解?Rtz0+例:RL串联电路,-0时开关SUR+X闭合,u=Umcos(ot+Φu),A26求开关阴合厨i0-?资料!解:由KVL得di+ Rii= Umcos(ot+ Φu)dt其通解为:i=i'+i"请勿其中i'为其特解,i"为其对应的齐次微分方程通解。公
SDUT 内 部 资 料! 请 勿 外 传! 思考:一阶电路中,激励不是恒定直流,而是正弦电 压,响应如何求解? 例:RL串联电路,t=0时开关 闭合 ,us =Umcos(wt+u ), 求开关闭合后,i(t)=? t≥0+ us + - + -uL R L i + uR - L diL dt + RiL= Umcos(wt+ u ) 其通解为: iL= iL '+ iL '' 解:由KVL得 其中 iL ' 为其特解, iL ''为其对应的齐次微分方程通解

Rt≥0.OORi= Umcos(ot $.)UR+us其通解为:i=i+i'R(1)先求特解iu,=Umcos(at+du)特解的形式:i=Imcos(ot+の)di'+ Rin Un数(a+ 0.)则dt-のLImsin(ot+)+RImcos(ot+0) =Umcos(ot+ Φu)整理得Im[R cos(αt + 0) - oL sin(at+ )] = U m cos(ot + d.)勿外传!
SDUT 内 部 资 料! 请 勿 外 传! dt us =Umcos(wt+u ) L R t = t≥0+ us + - + -uL R L i + uR - (1)先求特解iL ' 特解的形式:i' L= Imcos(wt +q ) -wLImsin(wt+q ) +RImcos(wt+q ) =Umcos(wt+ u ) 则 L di' L + Ri' L = Umcos(wt+ u ) [ cos( ) sin( )] cos( ) m w +q -w w +q = w + u I R t L t U t m 整理得 L diL dt + RiL= Umcos(wt+ u ) 其通解为: iL= iL '+ iL

Im[R cos(αt + O) - oL sin(ot + 0)] = Um cos(ot + d.)SDUTaLI. :R?+(oL)[cos(ot + 0)sin(ot + O)) = U cos(ot + d.R2 +(oL)R2 + (oL)I m ' R? + (oL)lcos @ cos(ot + 0)-sin p sin(αot +O)) = U m cos(ot + d.)部Rcos(ot+0+Φ)其中cos=令Z|= /R2 +(oL)2““料!R* +(oL)?aL则Im zcos(ot + 0 + p) = Um cos(ot + d.)sin@=/R? +(oL)2Imz|=Um, +=d.Ur因此特解:it=Imcos(at +ocos(at + Φu-Φ)玄外传!
SDUT 内 部 资 料! 请 勿 外 传! [ cos( ) sin( )] cos( ) m w +q -w w +q = w + u I R t L t U t m sin( )] cos( ) ( ) cos( ) ( ) ( ) [ u 2 2 2 2 2 2 m w q w w w w q w w + = + + + - + + t U t R L L t R L R I R L m ( ) [cos cos( ) sin sin( )] cos( ) u 2 2 Im R + wL wt +q - wt +q = Um wt + cos(wt+q +) 2 2 2 2 ( ) sin , ( ) cos R L L R L R w w w + = + 2 2 其中 = 令Z = R + (wL) cos( ) cos( ) m w +q + = w + u I Z t U t 则 m m = q + = u I Z U m , |Z| Um 因此特解:i' L = Imcos(wt +q ) = cos(wt + u-)

Um特解:ii=Imcos(ot +の)=cos(t + Φu-p)[2oTAe-!·再求通解iUmT.cos(ot+ Φu-p)+ A ei=i+i"R[Z]OOUR由i(0+)0定出;+++部资1usuiUmL类则cos(Φu-Φ)T=A=R[2]UUmmcos(u-) e-cos(ot+ Φu-P)LL=UR=RiL[Z][Zdi,ui=L暂态分量"随时稳态分量讠是与外加dt间的增长衰臧为零。激励同频率的正弦量外传!
SDUT 内 部 资 料! 请 勿 外 传! |Z| Um 特解:i' L = Imcos(wt +q ) = cos(wt + u-) |Z| Um iL = cos(wt+ u-)+ A e - t t 由iL (0+ ) = 0定出: A = - |Z| Um cos( u-) |Z| Um iL = cos(wt+ u-)- cos( u-) e |Z| Um - t t 稳态分量i‘ L是与外加 激励同频率的正弦量 暂态分量i" L随时 间的增长衰减为零。 l再求通解iL '' iL '+ iL '' = A e - t t L R t = us + - + -uL R L i + uR - uR = R iL uL= L diL dt 则
第8章相量法SDUT本章目录K立8.1复数8.2正弦量8.3相量法的基础8.4电路定律的相量形式传!
SDUT 内 部 资 料! 请 勿 外 传! 第8章 相量法 8.1 复数 8.2 正弦量 8.3 相量法的基础 8.4 电路定律的相量形式 本章目录