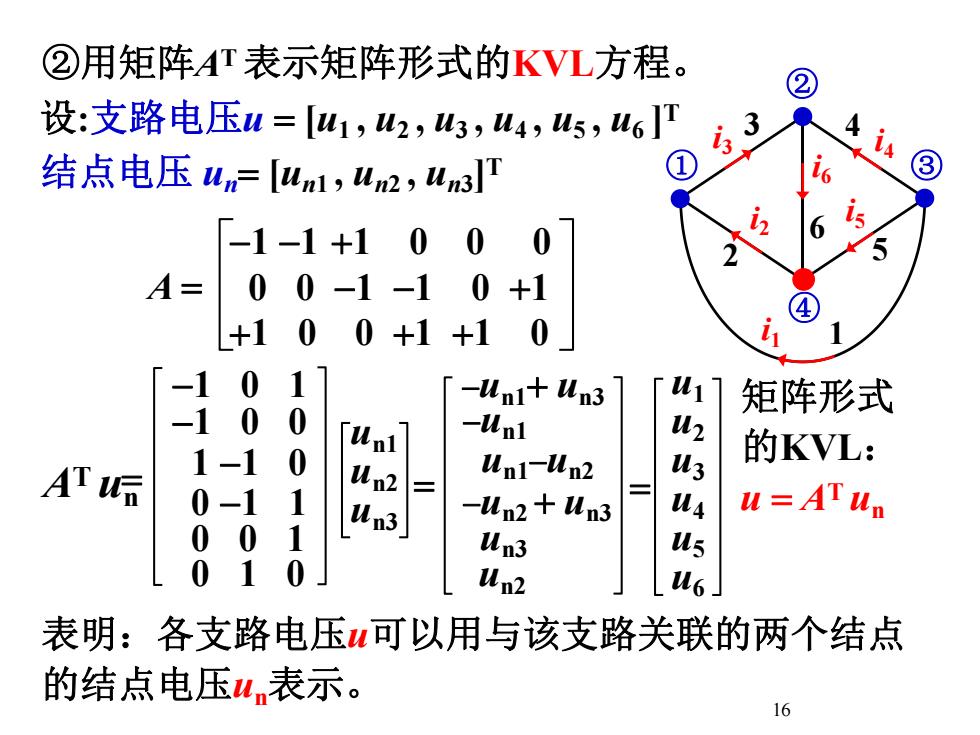
②用矩阵AT表示矩阵形式的KVL方程②设:支路电压u=[ui,u2,u3,4,us,u]T3N13①③结点电压 un=[uni,un2,un3]TL6is26000+1-1-152000-1-1+1A=400.0 +1L+1+110-1ui-uni+ Un3矩阵形式00-1u2-unl[un]的KVL:01-1usUn1-un2Un2AT u=u=ATun0-11us-Un2 + Un3Un3001usUn30011Un2u6.表明:各支路电压u可以用与该支路关联的两个结点的结点电压u,表示。16
16 0 1 0 ②用矩阵AT表示矩阵形式的KVL方程。 AT un un1 un2 un3 -1 0 0 1 -1 0 取④为参考结点, 结点电压与支路电压之间的关系为 结点①~③的 电压列向量 un [un1 , un2 , un3 ]T A -1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 1 1 0 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ -un1 un3 -un1 un1-un2 -un2 un3 un3 un2 u AT un 矩阵形式 的KVL: u1 u2 u3 u4 u5 u6 结点电压 un [un1 , un2 , un3]T 表明:各支路电压u可以用与该支路关联的两个结点 的结点电压un表示。 -1 0 1 0 0 1 0 -1 1 设:支路电压u [u1 , u2 , u3 , u4 , u5 , u6 ]T

描述独立回路与支路的关联性质2.回路矩阵B一支路b独立回路每一行对应一个独立回路,× bB =每一列对应一条支路。1(1)矩阵B的每一个元素定义为:+1,支路k与回路i关联,且方向一致-1,支路k与回路i关联,且方向相反k=30,支路k不在回路i中(无关)。方向一致+1,方向相反-1,无关0。bjk:17
17 2. 回路矩阵B 每一行对应一个独立回路, B = l b 独 立 回 路 l 支路b 每一列对应一条支路。 (1)矩阵B的每一个元素定义为: bjk 1, 支路 k 与回路 j 关联,且方向一致; -1, 支路 k 与回路 j 关联,且方向相反; 0, 支路 k 不在回路 j 中(无关)。 bjk:方向一致1,方向相反-1,无关0。 ——描述独立回路与支路的关联性质

例:求其回路矩阵B233LA3is652A18
18 i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ 例:求其回路矩阵B
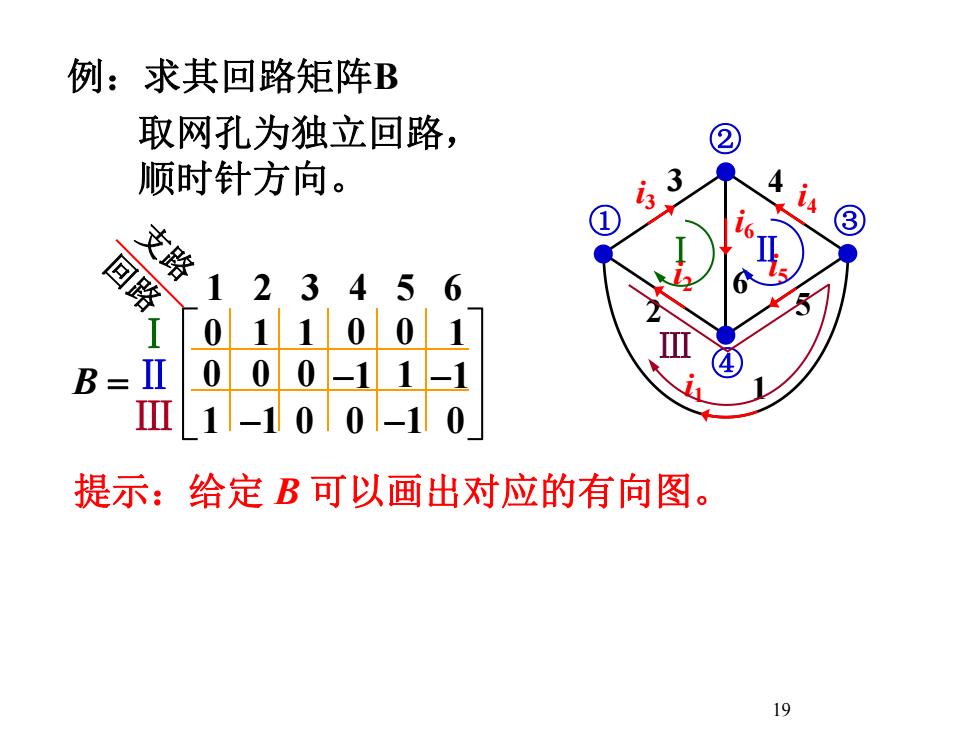
例:求其回路矩阵B取网孔为独立回路顺时针方向。+1支路回路623A-I0-0III40II00-1B=iIII1提示:乡给定B可以画出对应的有向图19
19 Ⅰ Ⅱ Ⅲ 1 2 3 4 5 6 0 Ⅰ 1 1 0 0 1 0 0 0 -1 1 -1 1 -1 0 0 -1 0 B i1 1 2 i2 3 i3 4 i4 5 i5 i6 6 ① ② ③ ④ Ⅱ Ⅲ 取网孔为独立回路, 顺时针方向。 回路 支路 提示:给定 B 可以画出对应的有向图。 例:求其回路矩阵B
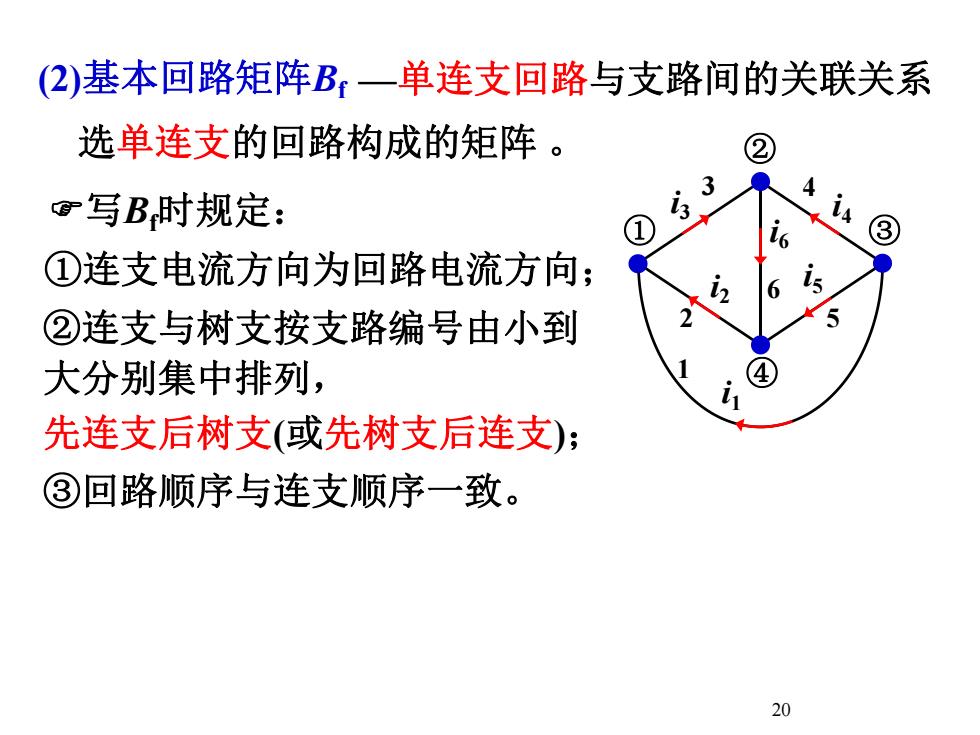
(2)基本回路矩阵B一单连支回路与支路间的关联关系选单连支的回路构成的矩阵。24G写B,时规定:13l6①连支电流方向为回路电流方向;i262②连支与树支按支路编号由小到4大分别集中排列i先连支后树支(或先树支后连支)③回路顺序与连支顺序一致。20
20 (2)基本回路矩阵Bf 选单连支的回路构成的矩阵 。 —单连支回路与支路间的关联关系 ①连支电流方向为回路电流方向; ②连支与树支按支路编号由小到 大分别集中排列, 先连支后树支(或先树支后连支); 写Bf时规定: ③回路顺序与连支顺序一致。 1 3 i3 4 i4 i6 6 ① ② ③ ④i1 2 i2 5 i5