
电 路义原义理 第2章线性电阻网络分析 本章以线性电阻网络为例,介绍分析线性电路的一般方法和电路定理。 一般方法是选择一组电路未知变量列写电路方程进行求解的方法。电路定 理主要包括替代定理、叠加定理、等效电源定理、互易定理等。这些方法和 定理在电路分析中具有普遍应用意义
第2章 线性电阻网络分析 本章以线性电阻网络为例,介绍分析线性电路的一般方法和电路定理。 一般方法是选择一组电路未知变量列写电路方程进行求解的方法。电路定 理主要包括替代定理、叠加定理、等效电源定理、互易定理等。这些方法和 定理在电路分析中具有普遍应用意义。 电 路 原 理

电 路义原义理 2.1支路电流法
电 路 原 理 2 . 1 支路电流法

上一章学习了依据元件特性和基尔霍夫定律、同时运用一些等效变换化简 电路的方法进行电路的分析计算。这些方法在分析复杂电路时不便于对电路进行 一般性的分析,因而对复杂电路的分析需要系统化的一般方法。系统化的一般方 法是选择一组电路变量(电流或电压),建立电路变量的方程进行求解的方法。 在这类方法中,支路电流法最为直接,并具有普遍适用性。支路电流法是 以支路电流为电路变量,应用KCL和KVL,列出与支路数相等的独立方程,然 后解出各支路电流的方法
上一章学习了依据元件特性和基尔霍夫定律、同时运用一些等效变换化简 电路的方法进行电路的分析计算。这些方法在分析复杂电路时不便于对电路进行 一般性的分析,因而对复杂电路的分析需要系统化的一般方法。系统化的一般方 法是选择一组电路变量(电流或电压),建立电路变量的方程进行求解的方法。 在这类方法中,支路电流法最为直接,并具有普遍适用性。支路电流法是 以支路电流为电路变量,应用KCL和KVL,列出与支路数相等的独立方程,然 后解出各支路电流的方法
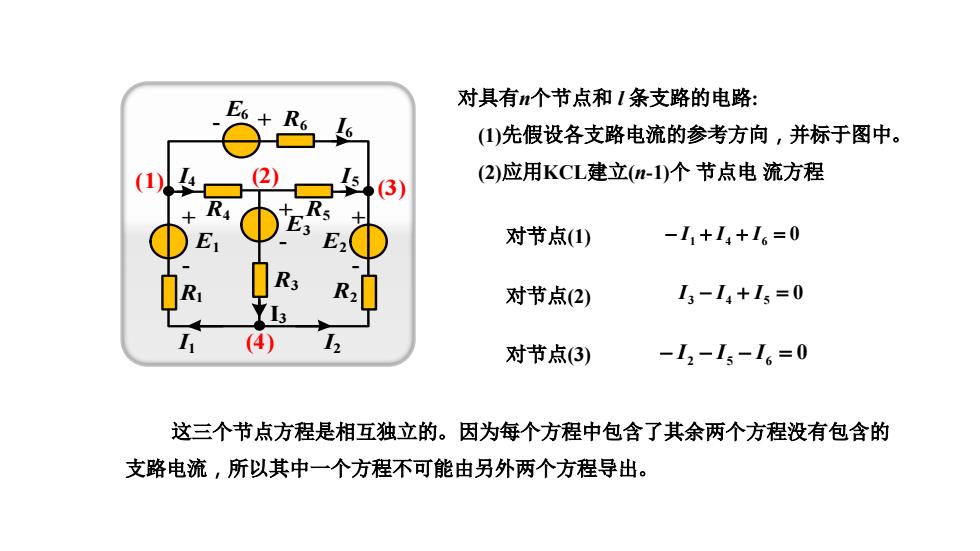
对具有个节点和1条支路的电路: ()先假设各支路电流的参考方向,并标于图中。 (1 (2)应用KCL建立(-1)个节点电流方程 3) 对节点() -L1+I4+I6=0 对节点(2) I3-14+I3=0 (4) 对节点3) -I2-I5-I6=0 这三个节点方程是相互独立的。因为每个方程中包含了其余两个方程没有包含的 支路电流,所以其中一个方程不可能由另外两个方程导出
对具有n个节点和 l 条支路的电路: (1)先假设各支路电流的参考方向,并标于图中。 E6 - + R6 E1 - + E3 - + E2 - + R1 R2 R3 R4 R5 I1 I2 I3 I4 I5 I6 (4) (3) (1) (2) (2)应用KCL建立(n-1)个 节点电 流方程 对节点(1) 对节点(2) 对节点(3) I1 I4 I6 0 I3 I4 I5 0 I2 I5 I6 0 这三个节点方程是相互独立的。因为每个方程中包含了其余两个方程没有包含的 支路电流,所以其中一个方程不可能由另外两个方程导出

如果对节点④再列一个方程,四个方程就不再是独立的了,因为对节点④列 出的节点方程是上列3个节点方程相加的结果。由此可见,具有四个节点的网络,应 用KCL,可以列出3个独立的节点方程,对应独立节点方程的节点称为独立节点。 推广到具有个节点的网络,理论上可以证明,独立的节点方程数(或独立节点数) 等于节点数减1,即(-1)个。这说明,对于有n个节点的网络,任选一个节点作参考节 点,其余(-1)个节点是独立节点,对这(-)个节点列出的方程是独立方程。 为求出图示电路的6个未知支路电流,在已列出3个独立节点方程的基础上,还需应 用KVL,建立其余三个方程
如果对节点 ④ 再列一个方程,四个方程就不再是独立的了, 因为对节点 ④ 列 出的节点方程是上列3个节点方程相加的结果。由此可见,具有四个节点的网络,应 用KCL,可以列出3个独立的节点方程,对应独立节点方程的节点称为独立节点。 推广到具有n个节点的网络,理论上可以证明,独立的节点方程数(或独立节点数) 等于节点数减1,即 (n-1) 个。这说明,对于有n个节点的网络,任选一个节点作参考节 点,其余(n-1) 个节点是独立节点,对这(n-1) 个节点列出的方程是独立方程。 为求出图示电路的6个未知支路电流,在已列出3个独立节点方程的基础上,还需应 用KVL,建立其余三个方程