边界上的电场 由介质分界面上电场强度切向分量连续的边界条件, 可知在处上下两部分电场强度满足: E(r)a,·a,=E2(r)a·a.→E(r)=E2(r)=E(r) ~在高斯面上应用高斯定理:[D=Q 2πr28,E,(r)+2πr282E2(r)=q →2πr2[8,+62]E(r)=9 q 82 →E(r)= 2x[8+62]r2 D(r)=&E(r) -电位移矢量为: D2(r)=82E(r) 16 lexu@mail.xidian.edu.cn
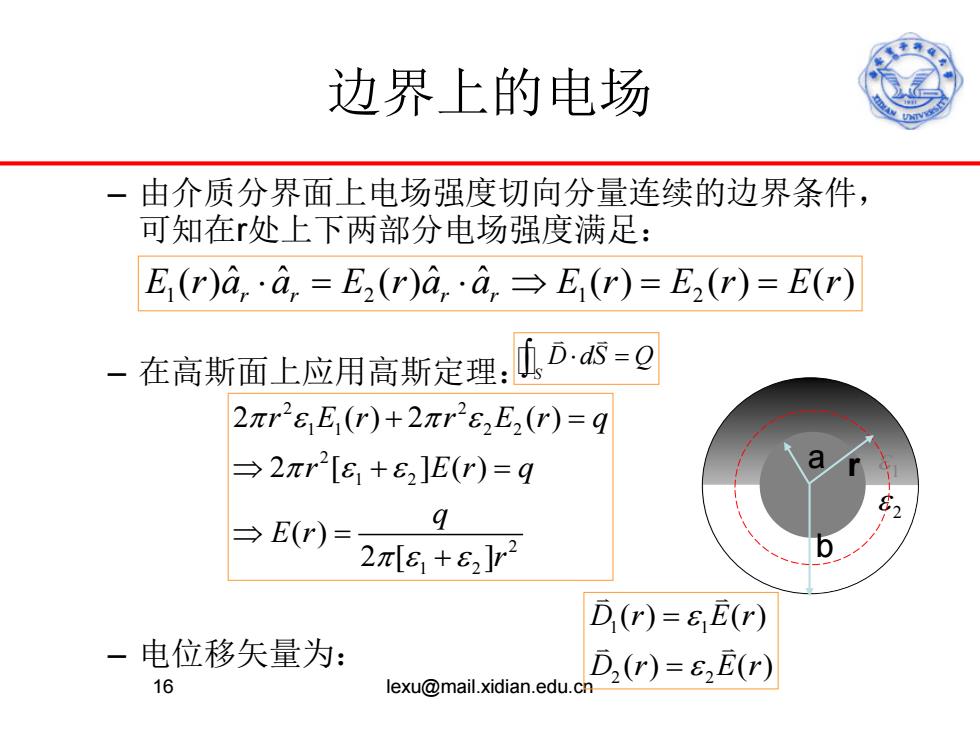
边界上的电场 – 由介质分界面上电场强度切向分量连续的边界条件, 可知在r处上下两部分电场强度满足: – 在高斯面上应用高斯定理: – 电位移矢量为: 16 lexu@mail.xidian.edu.cn a b 1 ε 2 ε r 1 2 12 () () () () () ˆ ˆ ˆ ˆ E ra a E ra a E r E r Er rr rr ⋅= ⋅⇒ = = S D dS Q ⋅ = ∫ 2 2 1 1 2 2 2 1 2 2 1 2 2 () 2 () 2 [ ] () ( ) 2[ ] r Er r Er q r Er q q E r r πε πε πεε πε ε + = ⇒+= ⇒ = + 1 1 2 2 () () () () D r Er D r Er ε ε = =

边界上的电场 -边界条件验证: ·介质边界上任取一点,显然电场强度切向连续; 电位移矢量法向连续(界面上无自由电荷): D2n Din=0 ·导体边界上任取一点,显然电场强度无切向分量, 即切向电场强度连续;内导体边界电位移矢量满足: i.D=a·a,eE(a=9 9 81+622na2 =P1 iD,=a,a,6,E(a)=62 9 81+632πa2 17 lexu@mail.xidian.edu.cn
边界上的电场 – 边界条件验证: • 介质边界上任取一点,显然电场强度切向连续; 电位移矢量法向连续(界面上无自由电荷): • 导体边界上任取一点,显然电场强度无切向分量, 即切向电场强度连续;内导体边界电位移矢量满足: 17 lexu@mail.xidian.edu.cn 2 1 0 D D n n = = 1 1 1 2 1 1 2 2 2 2 2 2 1 2 ˆ ˆ ˆ ( ) 2 ˆ ˆ ˆ ( ) 2 r r s r r s q nD a a Ea a q nD a a Ea a ε ε ρ εεπ ε ε ρ εεπ ⋅ =⋅ = = + ⋅ =⋅ = = +