
2)矢量积(矢量的叉乘 ) 任意两个矢量A与B的矢量积(ector Product)是一个矢量,矢量积的大小等于两 个矢量的大小与它们夹角的正弦之乘积,其 方向垂直于矢量A与B组成的平面,如图1-3 所示,记为 C=AX B-e,AB sin0 en-eaXeg(右手螺旋)
第一章 矢量分析 2) 矢量积(矢量的叉乘) 任 意 两 个 矢 量 A 与 B 的 矢 量 积 ( Vector Product)是一个矢量,矢量积的大小等于两 个矢量的大小与它们夹角的正弦之乘积,其 方向垂直于矢量A与B组成的平面, 如图1-3 所示,记为 C=A×B=enAB sinθ en=eA×eB (右手螺旋)
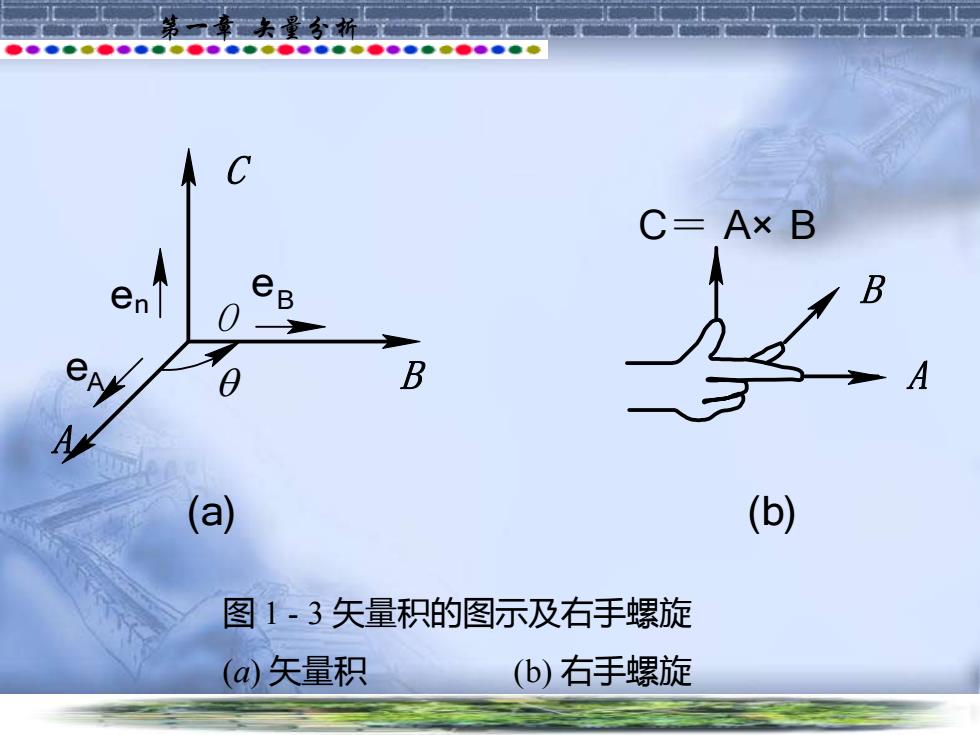
C=A×B e B D (a) (b) 图1-3矢量积的图示及右手螺旋 (a)矢量积 (b)右手螺旋
第一章 矢量分析 图 1 - 3 矢量积的图示及右手螺旋 (a) 矢量积 (b) 右手螺旋 C B A n eB A O C= A× B B A (a) (b) e e

矢量积又称为叉乘(Cross Product),如果两个 不为零的矢量的叉乘等于零,则这两个矢量 必然相互平行,或者说,两个相互平行矢量 的叉乘一定等于零。矢量的叉积不服从交换 律,但服从分配律,即 AXB=-BXA AX(B+C)=AXB+AXC
第一章 矢量分析 矢量积又称为叉乘(Cross Product),如果两个 不为零的矢量的叉乘等于零,则这两个矢量 必然相互平行,或者说,两个相互平行矢量 的叉乘一定等于零。矢量的叉积不服从交换 律,但服从分配律,即 A×B= -B×A A×(B+C)=A×B+A×C
直角坐标系中的单位矢量有下列关系式: exxey-e,eyxe,=ex exex-ey e, exxex=ey×e,=ezxe,=0 在直角坐标系中,矢量的叉乘还可以表示为 ev ex ey e: A×B= A A A B B B (4B.-AB)e(4.B,A B.)+e,(A B-AB)
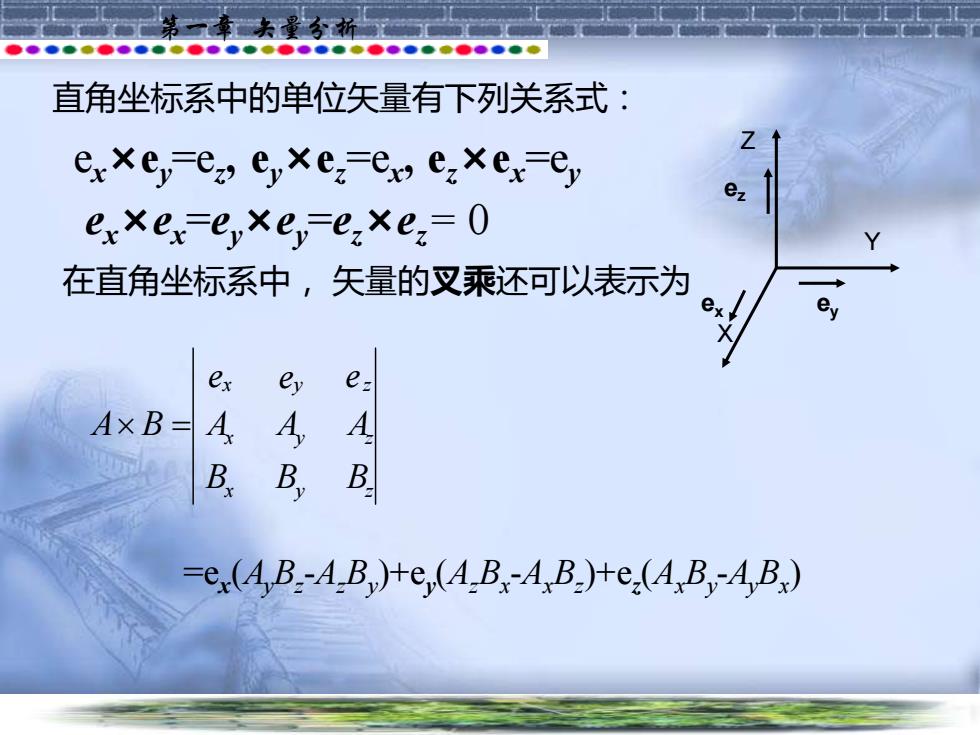
第一章 矢量分析 直角坐标系中的单位矢量有下列关系式: ex×ey=ez , ey×ez=ex , ez ×ex=ey ex×ex =ey×ey =ez ×ez = 0 在直角坐标系中, 矢量的叉乘还可以表示为 =ex (AyBz -AzBy )+ey (AzBx -AxBz )+ez (AxBy -AyBx ) x y z x y z x y z B B B A A A e A B = e e Z X Y ez ex ey

三、失量函数的导数与积分 矢量函数一般是空间坐标的函数,有时它也是时 间的函数。 1、矢量函数:若A的每个分量都是变量t的函数,则 称A是变量t的矢量函数。 2、矢量函数的导数:若极限1im A(t+△t)-A(@ 存在,则 称它为矢量函数A=A(t)的导数,总为: dA=dA (e dt dt (A) dt dt
第一章 矢量分析 三、矢量函数的导数与积分 矢量函数一般是空间坐标的函数,有时它也是时 间的函数。 1、矢量函数:若A的每个分量都是变量t 的函数,则 称A是变量t 的矢量函数。 2、矢量函数的导数:若极限 存在,则 称它为矢量函数A=A(t)的导数,记为: t 0 (t t)- (t) lim t → + A A x z y x y z d dA (t) dA (t) dA (t) e + e + e dt dt dt dt = A