
●●●●●●●●●● 在直角坐标系中,用单位矢量2,、已,、e表征矢量 分别沿x、y、轴分量的方向。 空间的一点A(X,Y,Z☑能够由它在三个相互垂直 的轴线上的投影唯一地被确定,如图1-1所示。 从原点指向点A的矢量下称为位置矢量 (Position Vector),它在直角坐标系中表示为 r =e.X+e Y+e.Z
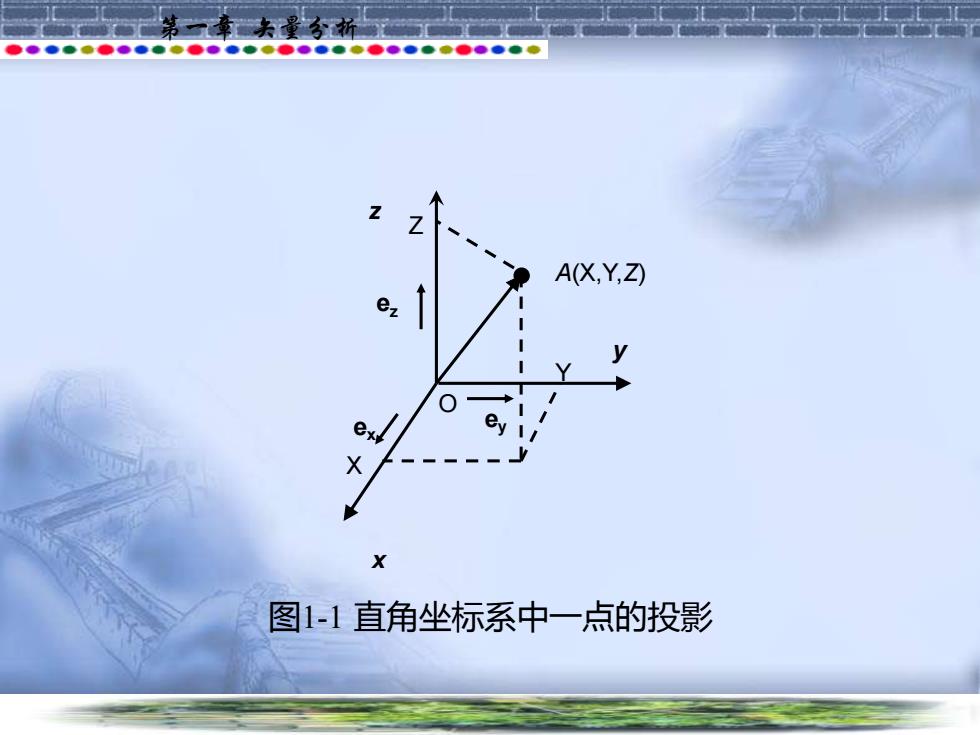
第一章 矢量分析 在直角坐标系中,用单位矢量 、 、 表征矢量 分别沿x、y、 z轴分量的方向。 空间的一点A(X,Y,Z)能够由它在三个相互垂直 的轴线上的投影唯一地被确定,如图1-1所示。 从原点指向点A的矢量 称为位置矢量 (Position Vector),它在直角坐标系中表示为 x e y e z e r r e e e = x y z X+ Y+ Z
A(X,YZ) 图11直角坐标系中一点的投影
第一章 矢量分析 图1-1 直角坐标系中一点的投影 z x e ey x ez y O A(X,Y,Z) Y Z X
二、矢量的加法和减法 矢量加、减符合平行四边形法则; 矢量的加减法:是两矢量对应坐标分量之和,矢量加 法的结果仍是矢量 A=exAx +eyAy+eA B=e,Bx +e,By +e,B A+B=e(Ax+B)+e(A,+B)+e(A,+B) A-B=e,(Ax-B)+e(Ay-B)+e(A.-B) “A+B月 A
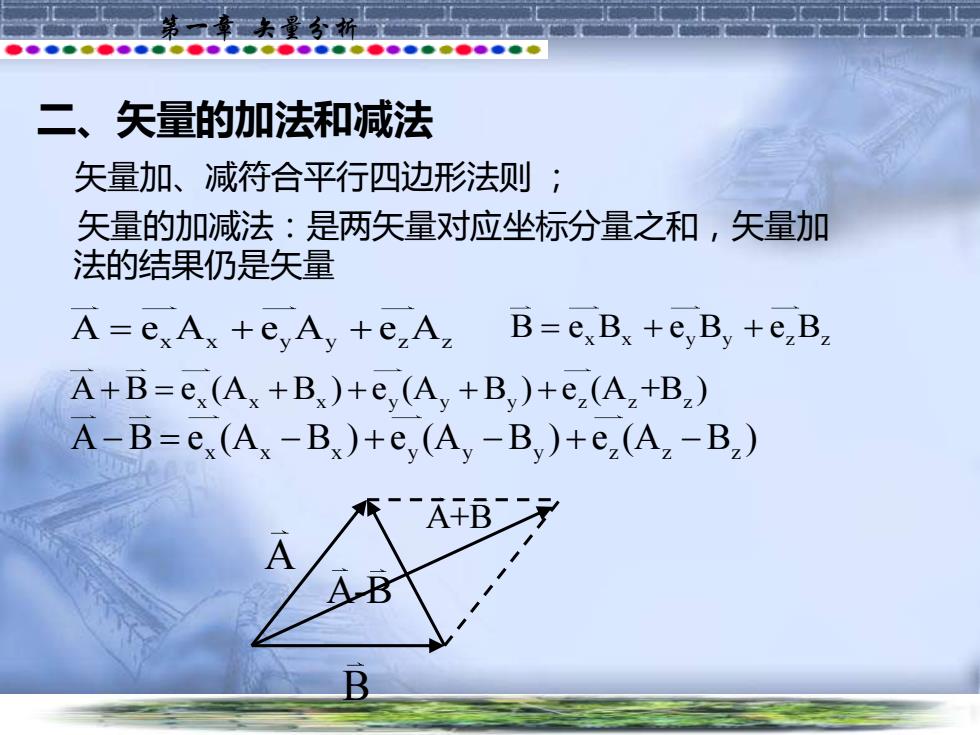
第一章 矢量分析 二、矢量的加法和减法 矢量加、减符合平行四边形法则 ; 矢量的加减法:是两矢量对应坐标分量之和,矢量加 法的结果仍是矢量 A e A e A e A = + + x x y y z z B e B e B e B = + + x x y y z z A B e (A B ) e (A B ) e (A +B ) + = + + + + x x x y y y z z z A B e (A B ) e (A B ) e (A B ) − = − + − + − x x x y y y z z z A B A+B A-B
1.1.3矢量的乘积 矢量的乘积包括标量积和矢量积。 1)标量积(矢量的点乘)》 任意两个矢量A与B的标量积 (Scalar Product)是一个标量, 它等于两个矢量的大小与它 们夹角的余弦之乘积,如图 1-2所示,记为 Bcos 0 A AB=AB cos0 图1-2标量积
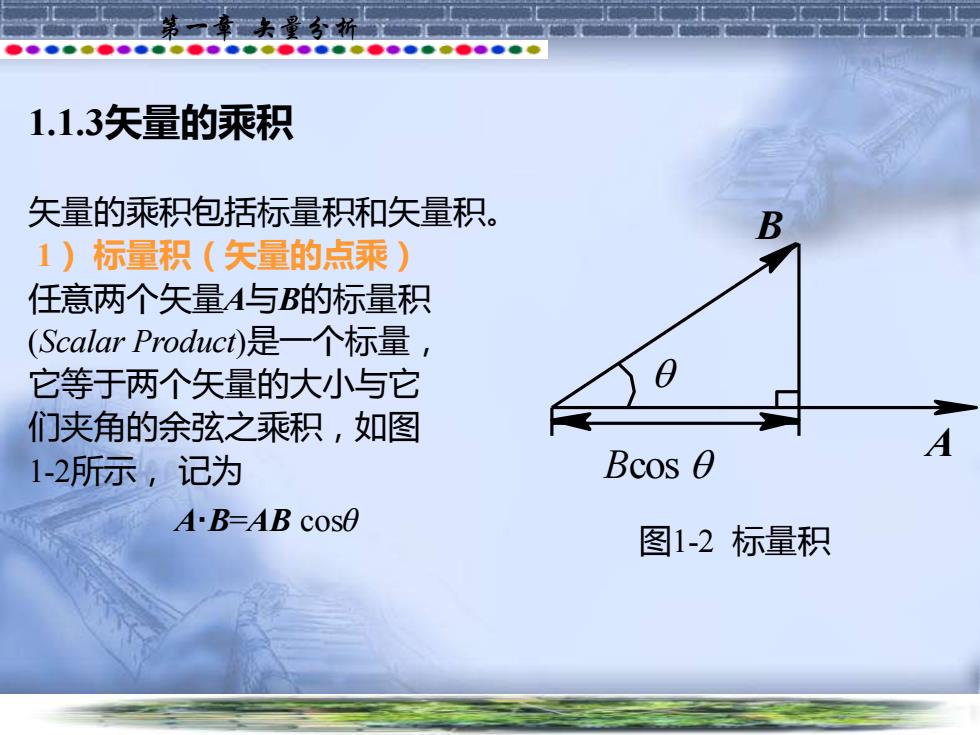
第一章 矢量分析 1.1.3矢量的乘积 矢量的乘积包括标量积和矢量积。 1) 标量积(矢量的点乘) 任意两个矢量A与B的标量积 (Scalar Product)是一个标量, 它等于两个矢量的大小与它 们夹角的余弦之乘积,如图 1-2所示, 记为 A·B=AB cosθ Bcos A B 图1-2 标量积

● 例如,直角坐标系中的单位矢量有下列关 系式: ex"e,-e,"e=exe,-0 ex'ex=ey'ey=e,e=1 任意两矢量的标量积,用矢量的三个分量 表示为 AB-A B,+A B+A.B. 标量积服从交换律和分配律,即 AB=BA A(B+C)=AB+AC
第一章 矢量分析 例如,直角坐标系中的单位矢量有下列关 系式: ex·ey =ey·ez = ex·ez=0 ex·ex =ey·ey =ez·ez=1 任意两矢量的标量积,用矢量的三个分量 表示为 A·B=AxBx +AyBy +AzBz 标量积服从交换律和分配律,即 A·B=B·A A·(B+C)=A·B+A·C