
在我们以后研究的有关内容中必将涉及到矢量函数随空 间坐标和时间的变化率问题,既对上述变量的偏导数问题 (CA.+A,+eA.) Ox 8x xx 一 -ex Ox ae+e⊙Ay+yOx 0e2 eyteAz+A2x ex Ox 矢量函数的积分包括不定积分和定积分两种,它们和一般函 数的积分在形式上类似,所以一般函数积分的基本法则对 矢量函数积分也适用
第一章 矢量分析 在我们以后研究的有关内容中必将涉及到矢量函数随空 间坐标和时间的变化率问题,既对上述变量的偏导数问题 x x y y z z x x z z y y x x y y z z x z y x y z A (e A e A e A ) A e A e A e e A e A e A A A A e e e x x x x x x x x x x x = + + = + + + + + = + + 矢量函数的积分包括不定积分和定积分两种,它们和一般函 数的积分在形式上类似,所以一般函数积分的基本法则对 矢量函数积分也适用
1.2三种常用的正交坐标系 1.2.1直角坐标系 e,=e xe. e..=e. 坐标变量: e.=e,xe M (xy) 变量取值范围: 0 单位矢量: (ex,e,e.) 任一矢量可表示为F=EF+E,F,+eF 图1.2.1直角坐标系 位置矢量:产=Ex+E,y+e2 di=e,dk+e,dy+e,d正 BACK
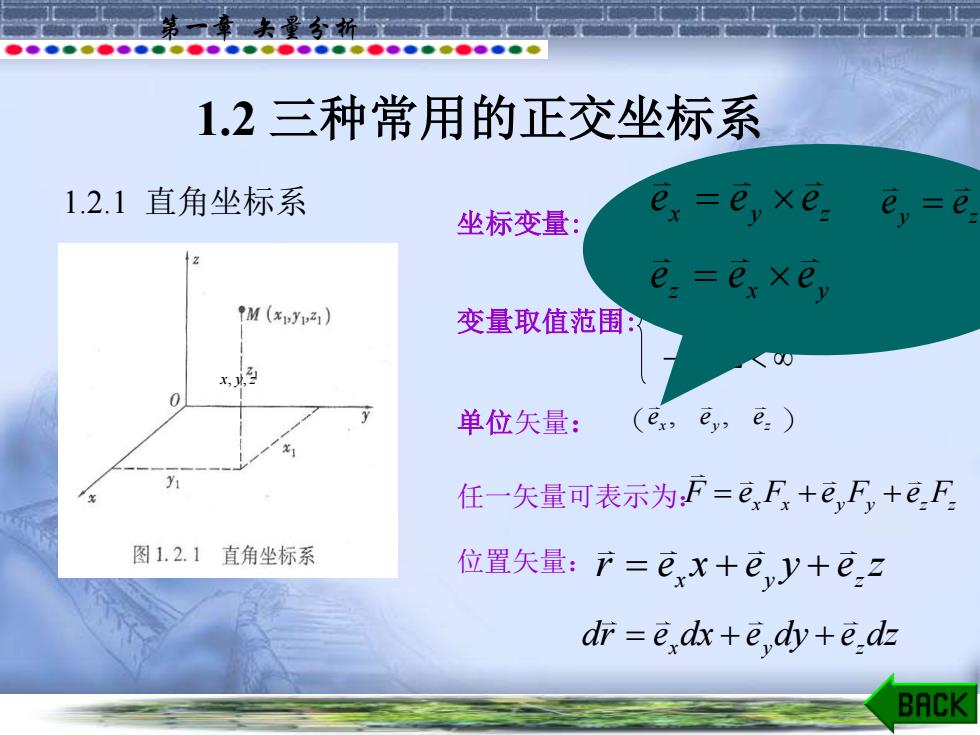
第一章 矢量分析 1.2 三种常用的正交坐标系 1.2.1 直角坐标系 坐标变量: 变量取值范围: 单位矢量: ( ) 任一矢量可表示为: 位置矢量: x, y,z x, y,z − y − x − z , , x y z e e e F e F e F e F = + + x x y y z z x y z r e x e y e z = + + x y z e e e = y z x e e e = z x y e e e = x y z dr e dx e dy e dz = + +