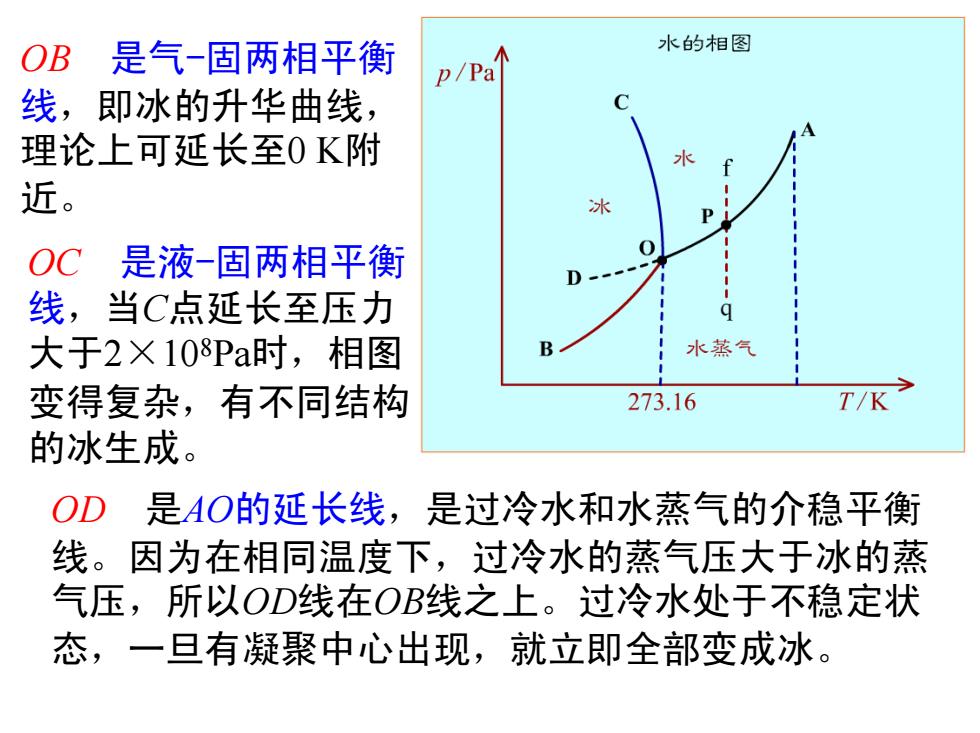
OB 是气-固两相平衡 水的相图 p/Pa 线,即冰的升华曲线, C 理论上可延长至0K附 水 近。 冰 P OC是液-固两相平衡 0 D 线,当C点延长至压力 大于2×108Pa时,相图 水蒸气 变得复杂,有不同结构 273.16 T/K 的冰生成。 OD 是AO的延长线,是过冷水和水蒸气的介稳平衡 线。因为在相同温度下,过冷水的蒸气压大于冰的蒸 气压,所以OD线在OB线之上。过冷水处于不稳定状 态,一旦有凝聚中心出现,就立即全部变成冰
OB 是气-固两相平衡 线,即冰的升华曲线, 理论上可延长至0 K附 近。 OC 是液-固两相平衡 线,当C点延长至压力 大于2×108Pa时,相图 变得复杂,有不同结构 的冰生成。 OD 是AO的延长线,是过冷水和水蒸气的介稳平衡 线。因为在相同温度下,过冷水的蒸气压大于冰的蒸 气压,所以OD线在OB线之上。过冷水处于不稳定状 态,一旦有凝聚中心出现,就立即全部变成冰
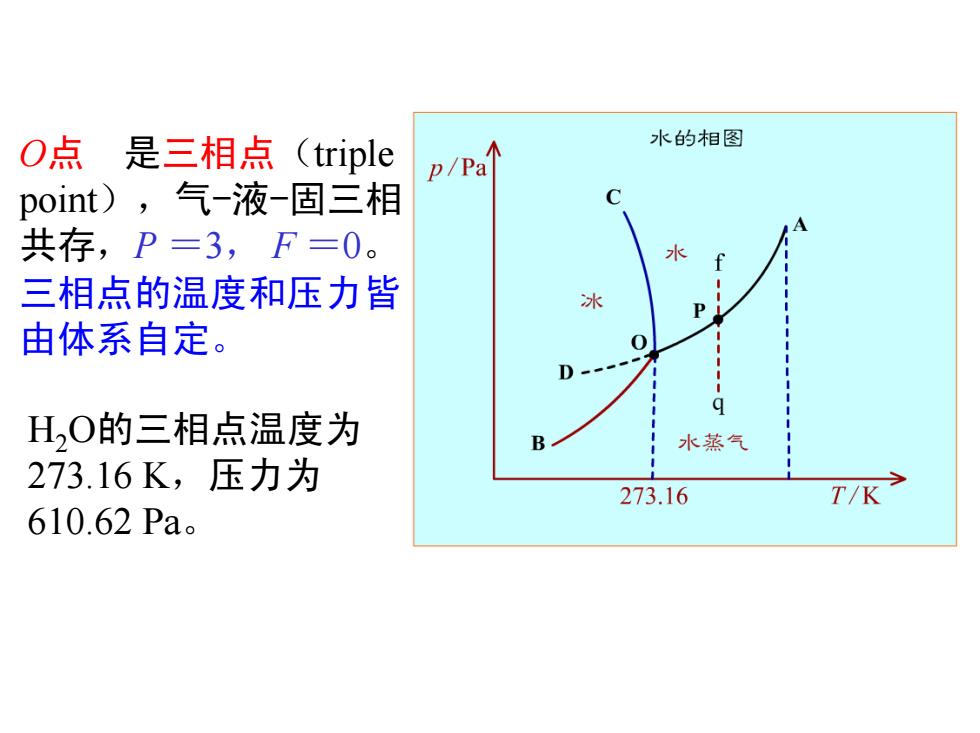
O点是三相点(triple 水的相图 P/Pan point),气-液-固三相 共存,P=3,F=0。 水 三相点的温度和压力皆 冰 由体系自定。 D- q HO的三相点温度为 水蒸气 273.16K,压力为 273.16 T/K 610.62Pa
O点 是三相点(triple point),气-液-固三相 共存,P =3, F =0。 三相点的温度和压力皆 由体系自定。 H2O的三相点温度为 273.16 K,压力为 610.62 Pa

两相平衡衡线上的相变过程 在两相平衡线上的任何一点都可能有三种情况。 如OA线上的P点: p/Pa 水的相图 (1)处于点的纯水,保持 温度不变,逐步减小压力, 在无限接近于P点之前,气 相尚未形成,系统自由度为 2。用升压或降温的办法保持 液相不变。 T/ (2)到达P点时,气相出现,在气-液两相平衡时, F=1。压力与温度只有一个可变。 (3)继续降压,离开P点时,最后液滴消失,成单一 气相,F=2
两相平衡线上的相变过程 在两相平衡线上的任何一点都可能有三种情况。 如OA线上的 P点: ( 1)处于f点的纯水,保持 温度不变,逐步减小压力, 在无限接近于 P点之前,气 相尚未形成,系统自由度为 2。用升压或降温的办法保持 液相不变。 ( 2)到达 P点时,气相出现,在气-液两相平衡时, F = 1。压力与温度只有一个可变。 ( 3)继续降压,离开 P点时,最后液滴消失,成单一 气相, F = 2

三相点与冰点的区别 p/Pa 水的相图 三相点是物质 自身的特性,不能 105 加以改变,如H,O 610.62 的三相点 T=273.16K, p=610.62Pa 273.15273.16 TK 冰点是在大气压力下,水、冰、气三相共存。当大 气压力为105Pa时,冰点温度为273.15K,改变外 压,冰点也随之改变
三相点与冰点的区别 三相点是物质 自身的特性,不能 加以改变,如 H 2 O 的三相点 T = 273.16 K , p =610.62 Pa 冰点是在大气压力下,水、冰、气三相共存。当大 气压力为 时,冰点温度为273.15K,改变外 压,冰点也随之改变。 5 10 P a
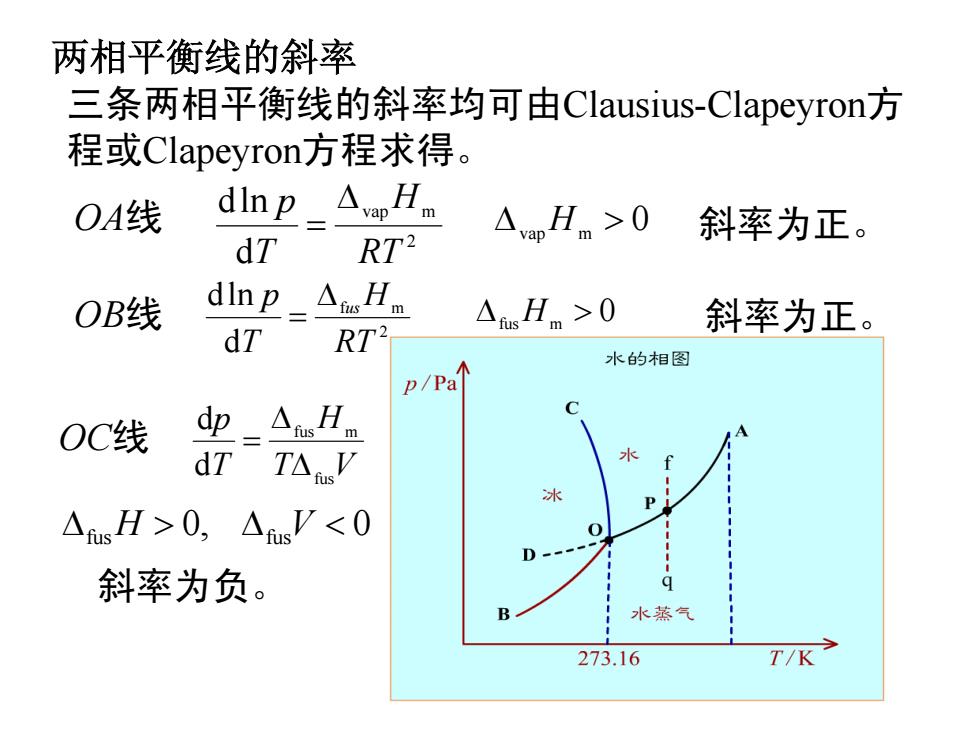
两相平衡线的斜率 三条两相平衡线的斜率均可由Clausius-Clapeyron方 程或Clapeyron?方程求得。 OA线 dIn p Avp Hm △anHm>0 斜率为正。 dT RT2 vap OB线 dlnp_△sHn △sHm>0 dT RT2 斜率为正。 水的相图 p/Pa个 OC线 dp_△sHm dT TAV △sH>0,△sV<0 斜率为负。 水蒸气 273.16 T/K
两相平衡线的斜率 三条两相平衡线的斜率均可由Clausius-Clapeyron 方 程或Clapeyron方程求得。 OA 线 2 vap m d dln RT H T p ∆ = ∆ vap H m > 0 斜率为正。 OB 线 2 f m d dln RT H T p ∆ us = 0 ∆fus H m > 斜率为正。 OC 线 T V H T p fus fus m d d ∆ ∆ = 斜率为负。 ∆ > fu sH V 0, ∆ fu s < 0