海南大学：《电路原理》课程教学资源（课件讲稿）第九章 正弦稳态电路的分析

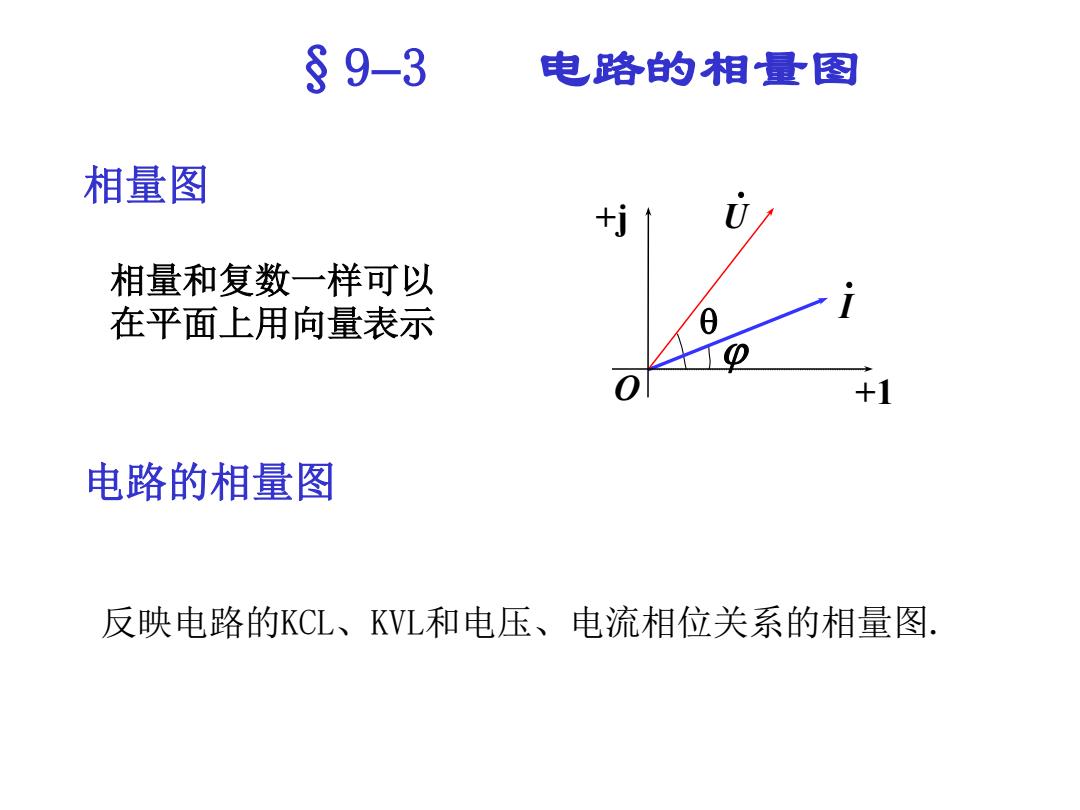
§9-3 电路的相量图 相量图 +j U 相量和复数一样可以 在平面上用向量表示 0 +1 电路的相量图 反映电路的KCL、KVL和电压、电流相位关系的相量图

§93 电路的相量图 相量和复数一样可以 在平面上用向量表示  q  U  I +1 +j O 相量图 电路的相量图 反映电路的KCL、KVL和电压、电流相位关系的相量图

§9-4， 正弦稳态电路的分析 电阻电路与正弦稳态电路相量法分析比较： 电阻电路： 正弦电路相量分析： KCL: ∑i=0 KVL:∑u=0 KCL:∑i=0 元件约束关系： u=Ri KL:∑U=0 或i=Gu 元件约束关系：U=zi 或1=YU 可见，二者依据的电路定律是相似的。只要作出正弦 稳态电路的相量模型，便可将电阻电路的分析方法推广到 正弦稳态电路的相量分析中

§94 正弦稳态电路的分析 电阻电路与正弦稳态电路相量法分析比较：              i Gu u Ri u i : KVL : 0 KCL : 0 : 或 元件约束关系 电阻电路 : KVL : 0 KCL : 0 :                      I Y U U Z I U I 或 元件约束关系 正弦电路相量分析 可见，二者依据的电路定律是相似的。只要作出正弦 稳态电路的相量模型，便可将电阻电路的分析方法推广到 正弦稳态电路的相量分析中

一、利用心=Zi或i=Y心求解 1.同一元件的阻抗与导纳互为倒数，同一对端口之间的阻抗与导 纳互为倒数，即 2.记住基本元件的阻抗和导纳 名.Zdd 3.串联部分总阻抗和并联部分的总导纳 k=1 k=1

一、利用 U   Z I  或 I   Y U  求解 1．同一元件的阻抗与导纳互为倒数，同一对端口之间的阻抗与导 纳互为倒数，即 2．记住基本元件的阻抗和导纳 3．串联部分总阻抗和并联部分的总导纳 Z Y Y Z 1 , 1   C j j C ZR R ZL j L ZC    1 1  ,  ,      n k Z Zk 1   n k Y Yk 1

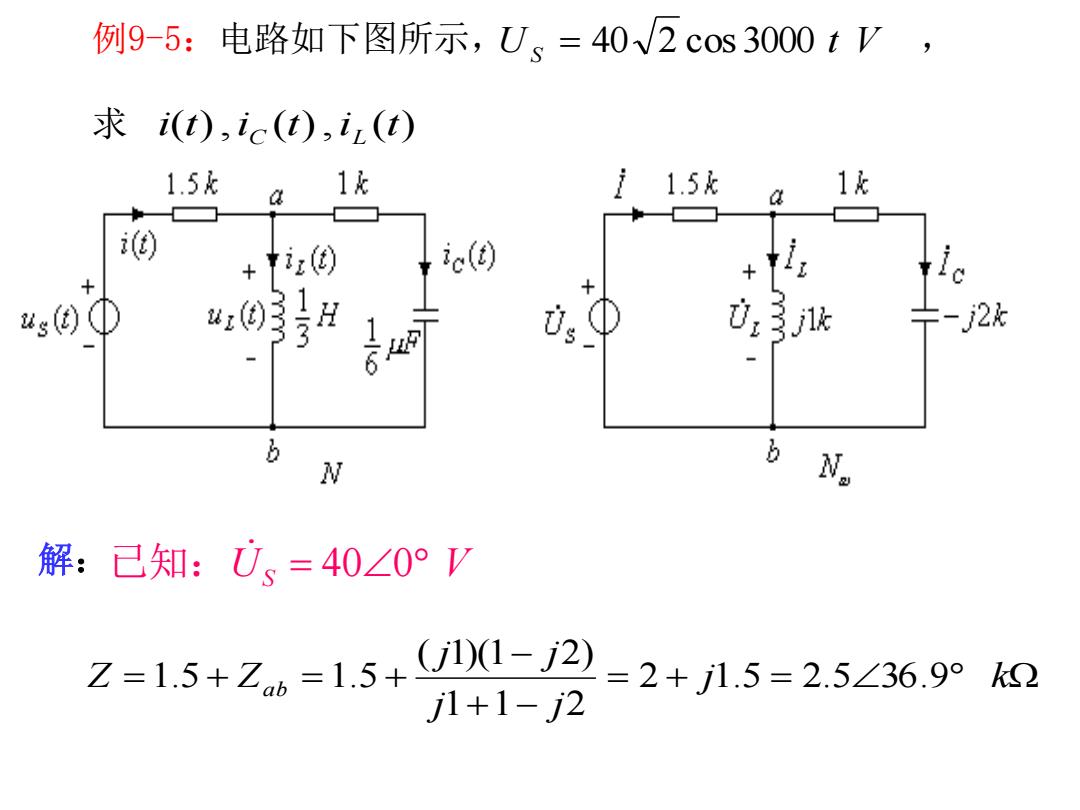
例9-5：电路如下图所示，U、=40√2cos3000tV, 求i(t),ic(t),iz(t) 1.5k i a 1k i 1.5k 1元 ) +z) tic() V: 卡-2 b N bN。 解：已知：U、=40∠0°V Z=1.5+26=1.5+101-j2 =2+1.5=2.5∠36.9°k2 1+1-2

例9-5：电路如下图所示， ， 求 US  40 2 cos 3000 t V i(t),i (t),i (t) C L 已知：U  S  400 V              j k j j j j Z Za b 2 1.5 2.5 36.9 1 1 2 ( 1)(1 2) 1.5 1.5 解：

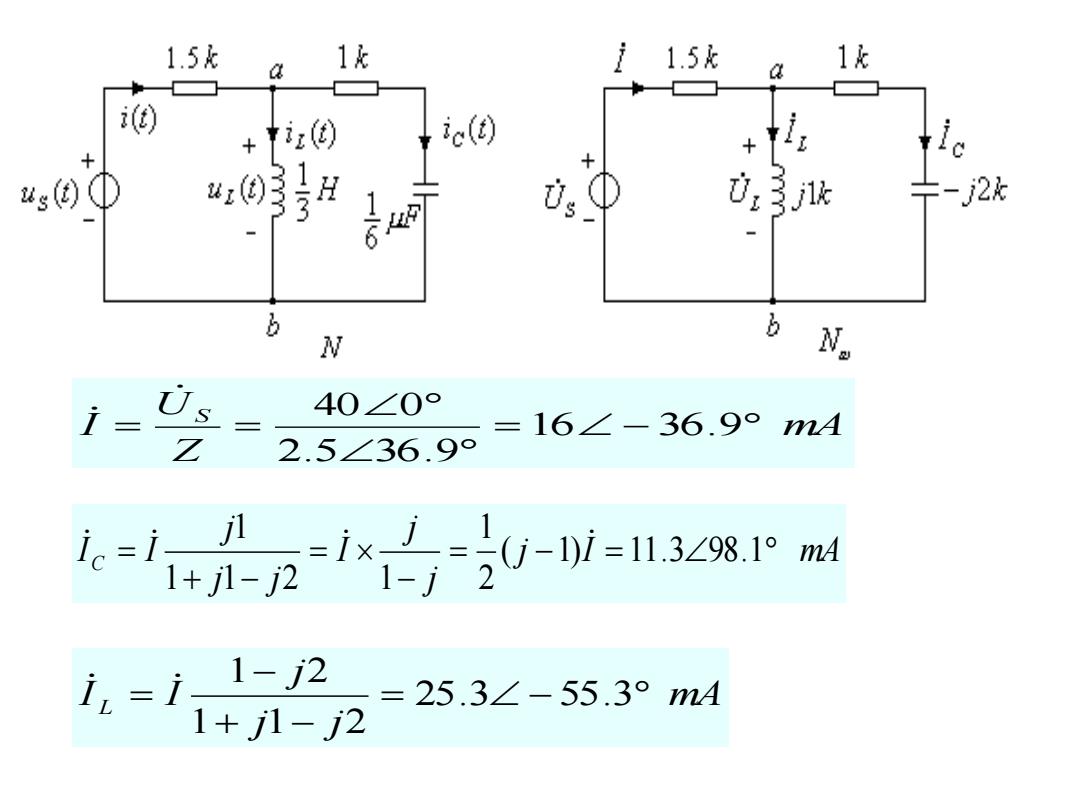
1.5k 1元 i1.5k 1k ④) +z ic() + c + 4s) U. 卡-j2 b N N i U 40∠0° 三 =16∠-36.9°mA Z 2.5∠36.9° i+21x-1-=I3zs网 ic=j- 1一 i,=i,1-2 =25.3∠-55.3°mA 1+1-2

mA Z U I S 16 36.9 2.5 36.9 40 0             j I mA j j I j j j I I C ( 1) 11.3 98.1 2 1 1 1 2 1 1                mA j j j I I L 25.3 55.3 1 1 2 1 2          