同济大学：《结构力学》课程教学资源（教案讲稿，打印版）16 Dynamic analysis of structures

2016/4/6 This numerical example shows that the transient response(瞬态响应)u(0 disappears after some time and that only the steady state response(稳态响应)u,( 8 is then left. u0=)+u() 0.4 u(t)=Ce-son sin(t+0 Po/k 0 sin(ot-) -(olenr]+Pi(olonP total response u(f) transient response u(f) C and 6 are determined by the initial conditions. For this case,the steady state is obtained after about 20 seconds 同桥大学 自土本2程学脱 Dynamic factor R can be plotted as function of the ratio After some while,the structure vibrates with for different values of the damping the same frequency as the applied force.It is coefficient片. the steady state response u(f). The amplitude of these vibrations are now 5=01 studied. 35 Up(t)= Po/k -sin(ot-6) =02 E=04 The static deformation due to a static load p ,l6-贤 5 253 The amplitude of the vibration is equal to (o/on) the product of the static deformation times a dimensionless(无量纲的) l0n<0.25→ RI "quasi static"response dynamic factor R miteu+ku=po sin(at)u=pol/k sin(at) Ra(s.olo)= 1 -(olen2}2+[25(@on】2 the amplitudes of vibrations become large:Resonance 11

2016/4/6 11     sin( ) ( ) ( ) ( ) C sin( ) o                   t p k u t t n n t D n 2 2 2 1 2 e This numerical example shows that the transient response ( 瞬 态 响 应 ) uh (t) disappears after some time and that only the steady state response(稳态响应)up (t) is then left.u(t) u (t) u (t)  h  p C and  are determined by the initial conditions. 0 5 10 15 20 25 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 t u total response u(t) transient response uh (t) For this case, the steady state is obtained after about 20 seconds.     sin( ) ( ) ( ) ( ) o            t p k u t n n p 2 2 2 1 2 k po o (ust)      1 R n n d n 2 2 2 1 ( ) 2 ( ) ( , )             n  0.25  Rd  1 "quasi static"response become large :Resonance the amplitudes of vibrations  n After some while, the structure vibrates with the same frequency as the applied force. It is the steady state response up (t). The amplitude of these vibrations are now studied. The static deformation due to a static load po is The amplitude of the vibration is equal to the product of the static deformation times a dimensionless（无量纲的） dynamic factor Rd . Rd can be plotted as function of the ratio  /n for different values of the damping coefficient . sin( ) sin( ) o o m u   c u   k u  p t  u  p k t 0 0.5 1 1.5 2 2.5 3 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5  = 0.1  = 0.2  = 0.4 Rd ( )  n Dynamic factor

2016/4/6 Resonance Example Resonance is reached for 5=2%→R。=25 The deformations are 25 times the static 0=4,=0nV1-25 ones. For this value of the dynamic factor is 1 25V-52 f<o.then Ramax*正and t n=ma。=n1-子,=an-252 冠问冷大学 1主本工程学汽 Duhamel's superposition integral General dynamic load j+o2y=P(D) m For an impulse PAt at time 0,if 1=0,S=PA,vo= S m ,%=0 →y=gsno1=P -sino t P() o Thus for an impulse PAt at timet,there is a displacement dS,=P()dt increment after time t. P(rd dy=- -sino(t-t） whent>r 7@ According to the principle of superp.osition(叠加原理) 1 y(t)= P(t)sin@(t-t)dr Initial condition(韧始条件)t=0:y=yo,y=o y(t)=yo cos@t+ 1 Yo sint+m P()sino(t-t)dt mo Jo @同冷大学 闺土本工相幸悦 12

2016/4/6 12 2      1 2 r n Resonance 2 2 1 1 2 2 1 0 1                   n n r n d k m R D if . then max and Example  2   25 Rd  % The deformations are 25 times the static ones. 2 2 1 1   Rd max  Resonance is reached for For this value of  , the dynamic factor is t m P t t m S y         sin sin 0, , 0    0  y0  m S t S P t v ， m P t y y ( ) 2 General dynamic load   0 0 t  0：y  y , y   v For an impulse Pt at time 0, if P(t) dτ τ t t dS  P(τ )dτ According to the principle of superposition(叠加原理) t τ t τ m P τ dτ dy      sin ( ) when ( ) P τ t τ dτ m y t t ( )sin ( ) 1 ( ) 0      P τ t τ dτ m t v y t y t t ( )sin ( ) 1 ( ) cos sin 0 0  0          Initial condition(初始条件) Thus for an impulse Pt at time , there is a displacement increment after time . Duhamel’s superposition integral

2016/4/6 Examples)Sudden oad(突加荷载) AP() [0,whent<0 P()= ,when≥0 y(t)= Po sino (t-t)dt P(1-cos@t) mo mo y=y (1-cos@t) 0 Dynamic factor:B=)=2 AP() (2)short-term load(短期荷载) 0,when t<0ort≥u P(1)= Po. when 0<t<u B。sino(t-t)dh y(t)= m00 0 Po[cos@(t-u)-cos@t] 1m0 y=ym×2sin Dynamic factor? @月务大学目土水程季我 3)Gradual load(渐变荷载) 本P(t) when0≤t≤t, P(t) P(t)= when t≥t, El 3EI k1 0 According to Duhamel's integral ()-me P(r)sin@(t-t)dt y= mo 2 Ia- sinot when t≤t t ∴ y= 1 y sinot-sin (t-t,) when t≥t, ot, 福月冷大学 1士本工程学晚 13

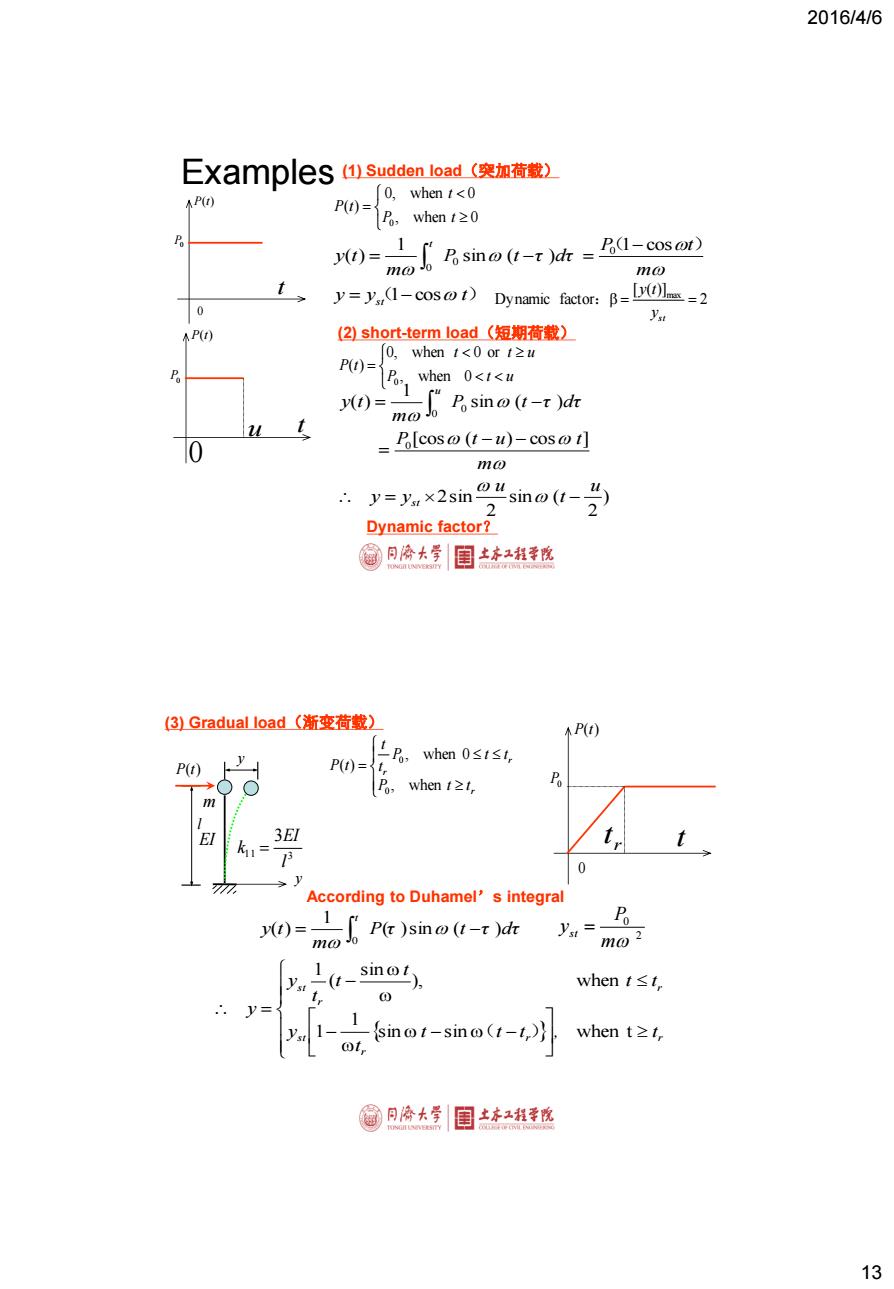
2016/4/6 13 (1) Sudden load（突加荷载） 2 [ ( )] Dynamic factor max    st y y t ：       , when 0 0, when 0 ( ) 0 P t t P t P(t) 0 t P0     m P t P t τ dτ m y t t （1 cos ） sin ( ) 1 ( ) 0 0 0      y  y（st 1cos t） (2) short-term load（短期荷载）         P t u t t u P t , when 0 0, when 0 or ( ) 0      m P t u t P t τ dτ m y t u [cos ( ) cos ] sin ( ) 1 ( ) 0 0 0       ) 2 sin ( 2 2sin u t u y y   st     P(t) 0 t P0 u Dynamic factor？ Examples          r r r P t t P t t t t P t , when , when 0 ( ) 0 0 (3) Gradual load（渐变荷载） P(t) 0 t P0 r t m EI y l 11 3 3 l EI k  y P(t)                             r r r s t r r s t t t t , t t y t t t t t y y sin sin when t 1 1 ), when sin ( 1 （ ） P τ t τ dτ m y t t ( )sin ( ) 1 ( ) 0      2 0 m P yst  According to Duhamel’s integral