
Chapter 11. Slope Deflection Method(转角变位移法) (and Other Equilibrium Methods). 月大学 自 土工程学院 TONGJI UNIERSITY 11.1 Nature of equilibrium methods Equilibrium The fundamental equations are methods the equations of equilibr Compatibility (平衡法) method(协调 法) Stiffness The fundamental equations are method (刚度法) composed of stiffness q Flexibility method(柔度 法) Displaceme The solution of the fund aa nt method (位移法) equations are displacemente Force method( 力法) 月大学 土木工程学院 TONGUNIVERSITY
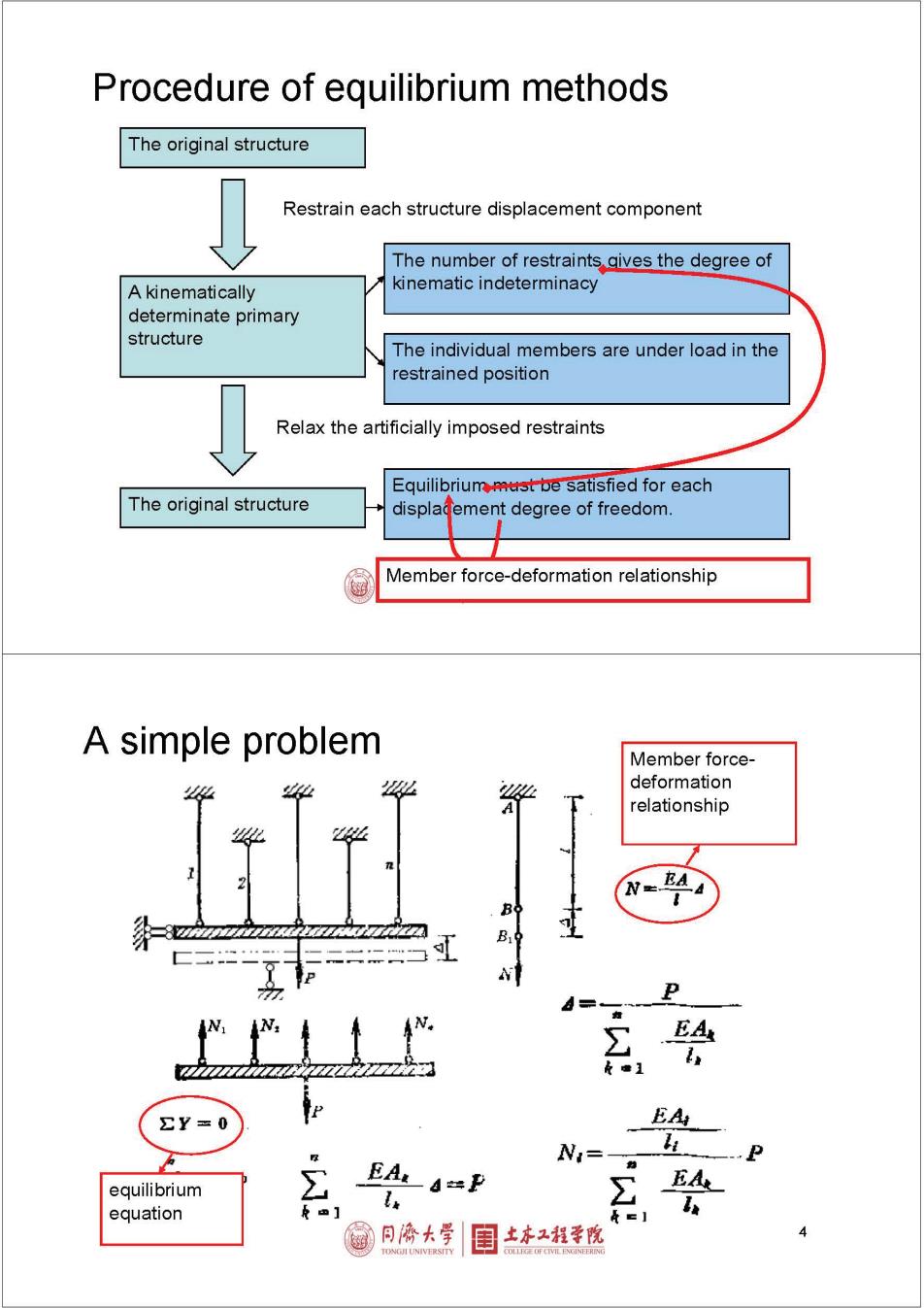
Procedure of equilibrium methods The original structure Restrain each structure displacement component The number of restraints qives the degree of A kinematically kinematic indeterminacy determinate primary structure The individual members are under load in the restrained position Relax the artificially imposed restraints Equilibrium must be satisfied for each The original structure displadement degree of freedom. Member force-deformation relationship A simple problem Member force- deformation relationship N=EAA B P EA Y=0 EA N,= equilibrium xd=P EAx equation L 冠月海大学 土床工程学院
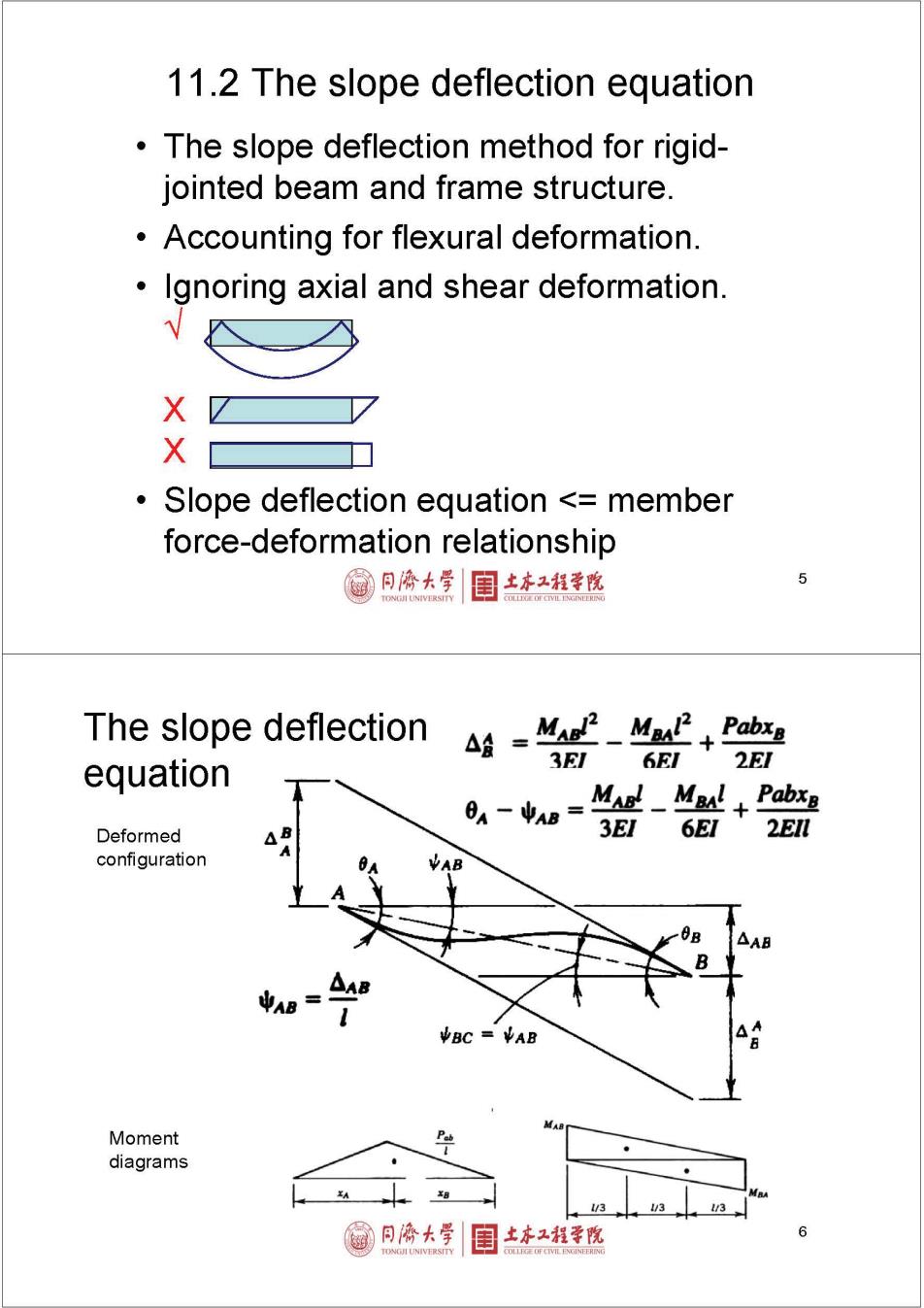
11.2 The slope deflection equation The slope deflection method for rigid- jointed beam and frame structure. Accounting for flexural deformation. Ignoring axial and shear deformation. X X Slope deflection equation <member force-deformation relationship @同傍大学目土本红程幸院 The slope deflection △8 MABl2 MRAP2 Pabxp equation 3EI 6EI 0A-中AB= MAnl MaAl Pabxe Deformed 3E1 6EI 2EIl configuration y 中AB BC VAB Moment diagrams /3 3 1/3 同僑大学 土本工程学院 6

The slope 0-AB= MAR!MRAL Pabxg deflection 3E1 6EI 2EIl M过+M然 Pabx equation 6EI 3EI 2Ell continued The slope deflection equation MA8-Member-end moment 2E1 MAB (20+0-3)+FEMAm FEMAB-Fixed-end moment M2)FEM n-near end M=2EK(20+-3+FEM f-far end Krstiffness factor 4EI。,2E 。6E1 Knr=//,unit stiffness; Mg8+ 0- 24 stiffness per unit length; 线刚度 以份不子闺人 Fixed-end moments(固端弯矩) Loading MAB MBA -Pab2 +Pa2b -w2 +w2 12 2 +w2 20 晋-+) +b(2a-b) M +ab-告 国二
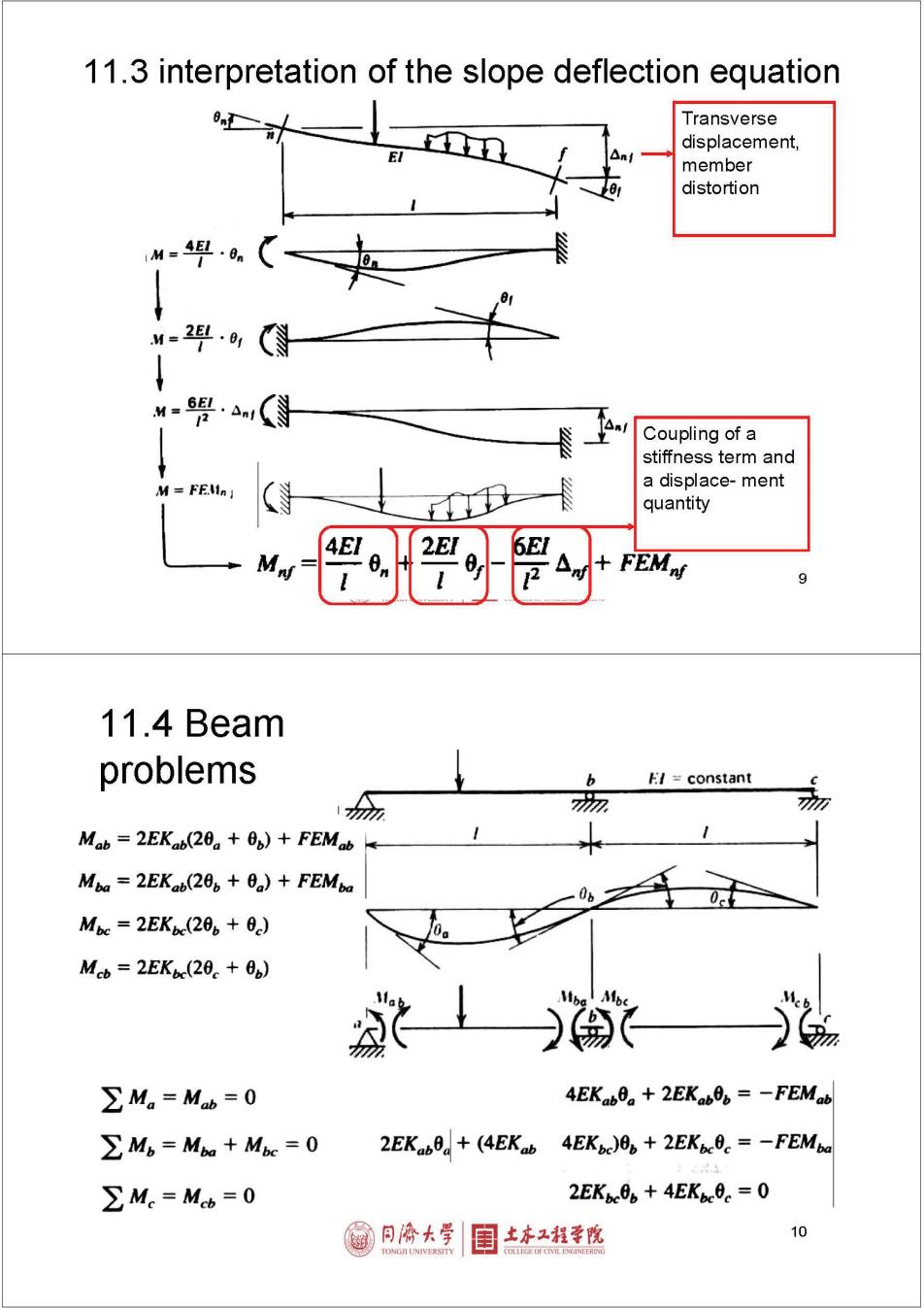
11.3 interpretation of the slope deflection equation Transverse displacement, member distortion M=4·9, M=24.9 /2 Coupling of a stiffness term and a displace-ment quantity 4EI FEMnf 9 11.4 Beam problems b /constant Mab 2EKab(20 +0p)+FEMab Mba 2EKab(20p+0a)+FEMba Mbc 2EKbe(20p+0c) Mcb=2EKc(20。+0b) ∑M。=Mb=0 4EKab0 2EKab0=-FEMab ∑M6=Mba+Mbc=0 2EKab0.+(4EKab4EKbc)8。+2EK0。=-FEMbo ∑Me=Mcb=0 2EKbe0。+4EKe0。=0 同榜大学 土床工程学院 10