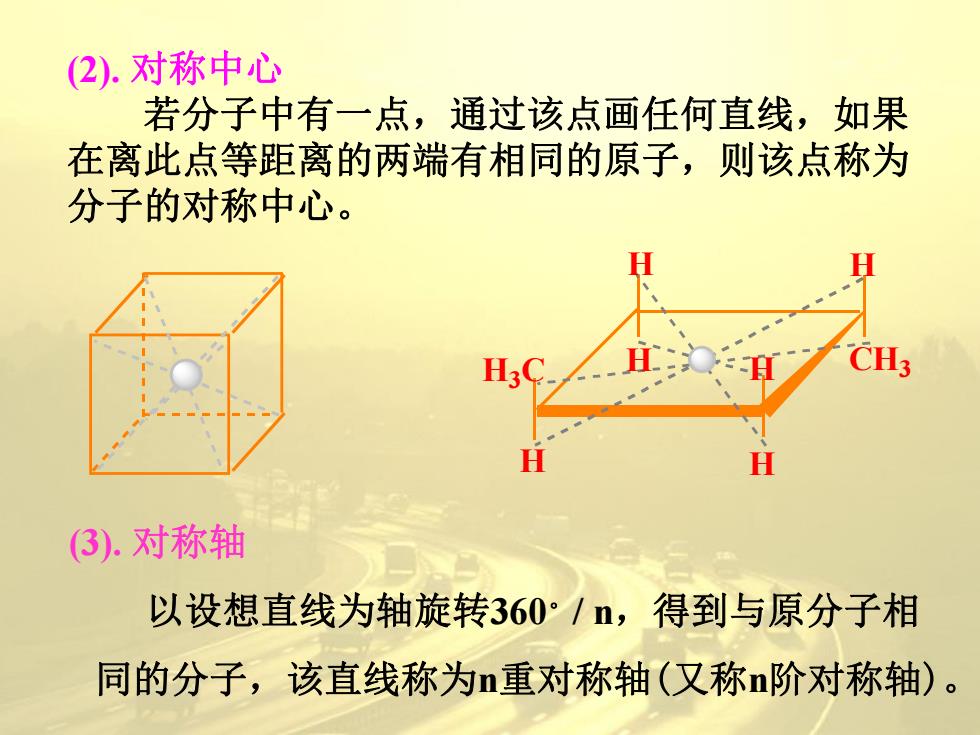
(2).对称中心 若分子中有一点,通过该点画任何直线,如果 在离此点等距离的两端有相同的原子,则该点称为 分子的对称中心。 H H (3).对称轴 以设想直线为轴旋转360°/n,得到与原分子相 同的分子,该直线称为n重对称轴(又称n阶对称轴)
(2). 对称中心 若分子中有一点,通过该点画任何直线,如果 在离此点等距离的两端有相同的原子,则该点称为 分子的对称中心。 H H H H H H H3C CH3 (3). 对称轴 以设想直线为轴旋转360。/ n,得到与原分子相 同的分子,该直线称为n重对称轴(又称n阶对称轴)

4四重交替对称釉(旋转反陕) 如果一个分子沿轴旋转90°,再用一面垂直于该轴的镜 子将分子反射,所得的镜像如能与原物重合,此轴即为该分 子的四重交替对称轴(用S4表示)。 90
C C Cl H Cl H (4). 四重交替对称轴(旋转反映轴) 如果一个分子沿轴旋转90 ,再用一面垂直于该轴的镜 子将分子反射,所得的镜像如能与原物重合,此轴即为该分 子的四重交替对称轴(用S4表示)。 H H Cl Cl H H Cl Cl 旋转 H H Cl Cl H Cl Cl H - - H H Cl Cl H H Cl Cl 90

结 A.有对称面、对称中心、交替对称轴的分子均可与 其镜象重叠,是非手性分子;反之,为手性分子。 对称轴并不能作为分子是否具有手性的判据。 B.大多数非手性分子都有对称轴或对称中心,只有 交替对称轴而无对称面或对称中心的化合物是少 数。 所以既无对稼面世没有对称神的x三股回判定 为是手性分哥
结论: A.有对称面、对称中心、交替对称轴的分子均可与 其镜象重叠,是非手性分子;反之,为手性分子。 对称轴并不能作为分子是否具有手性的判据。 B.大多数非手性分子都有对称轴或对称中心,只有 交替对称轴而无对称面或对称中心的化合物是少 数。 所以,既无对称面也没有对称中心的,一般可判定 为是手性分子
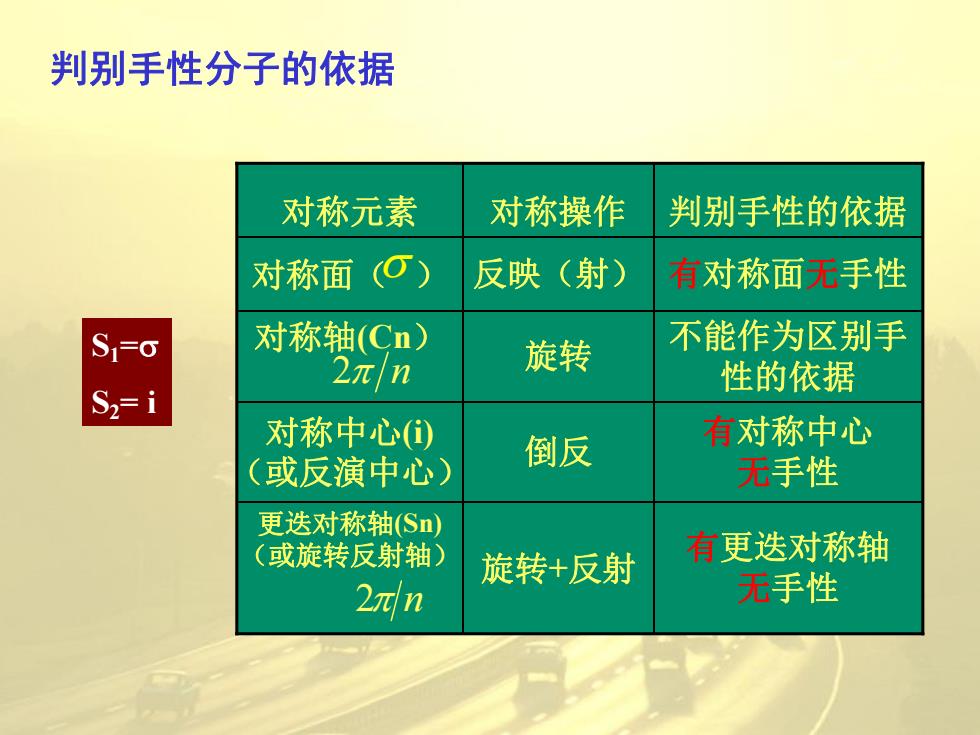
判别手性分子的依据 对称元素 对称操作 判别手性的依据 对称面 (O) 反映(射) 有对称面无手性 S1=o 对称轴(Cn) 2nn 旋转 不能作为区别手 性的依据 S2=i 对称中心① 有对称中心 (或反演中心) 倒反 无手性 更迭对称轴(Sn) (或旋转反射轴) 旋转+反射 有更迭对称轴 2xn 无手性
判别手性分子的依据 有更迭对称轴 无手性 旋转+反射 更迭对称轴(Sn) (或旋转反射轴) 有对称中心 无手性 倒反 对称中心(i) (或反演中心) 不能作为区别手 性的依据 旋转 对称轴(Cn) 对称面( ) 反映(射) 有对称面无手性 对称元素 对称操作 判别手性的依据 2 n 2 n S1= S2= i

四、含一个手性碳原子的化合物 还以乳酸为例,它含有一个手性碳原子,有 手性,具有旋光性,有一对对映体。发酵得到的 乳酸是左旋的,其比旋光度为[α]=-3.8°,肌肉 运动产生的乳酸是右旋的,其比旋光度为+3.8°。 从酸奶中得到的乳酸无旋光性,它是等量的左旋 乳酸和右旋乳酸的混合物,叫外消旋体(常用士或 d表示)。外消旋体是混合物
四、含一个手性碳原子的化合物 还以乳酸为例,它含有一个手性碳原子,有 手性,具有旋光性,有一对对映体。发酵得到的 乳酸是左旋的,其比旋光度为 ,肌肉 运动产生的乳酸是右旋的,其比旋光度为 。 从酸奶中得到的乳酸无旋光性,它是等量的左旋 乳酸和右旋乳酸的混合物,叫外消旋体(常用±或 dl表示)。外消旋体是混合物。 [ ] 20 o 3.8 D = o 3.8