1。对称分量法的基本原理 1.3物理解释 不对称三相系统分解为三个独立的对称系统:正序系统、负序系统和零序系统 iNo-f=iu 正序 负序 零序 各相序合成
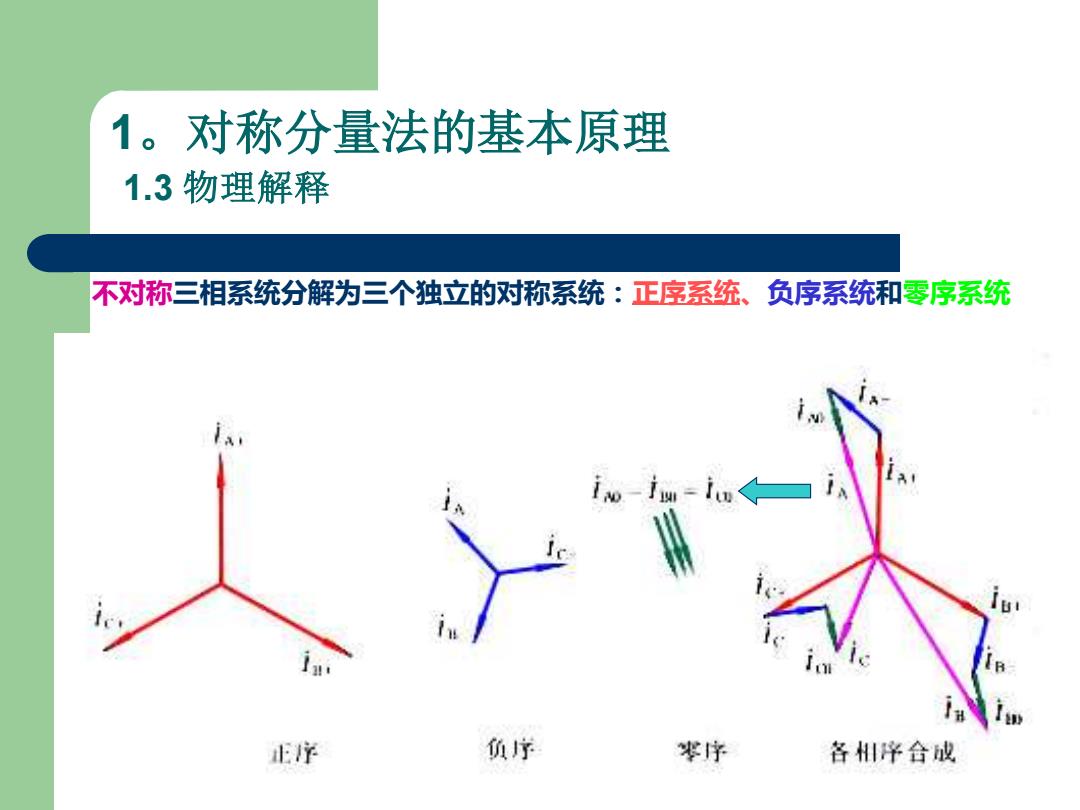
1。对称分量法的基本原理 1.3 物理解释 不对称三相系统分解为三个独立的对称系统:正序系统、负序系统和零序系统
1。对称分量法的基本原理 1.3物理解释例1 设有一不对称三相电压请将其分解为对称分量。 u4=V2.100cos(ot+30) 4B=V2.80cos(o1-60) 4e=V2.50cos(ot+90) U4=100∠30°=100(cos30°+jsin30)=86.6+j50 V Ug=80∠-60°=80(cos60°-jsin60)=40-j69.3 Uc=50∠90°=50(cos90°+jsin90)=0+j50W
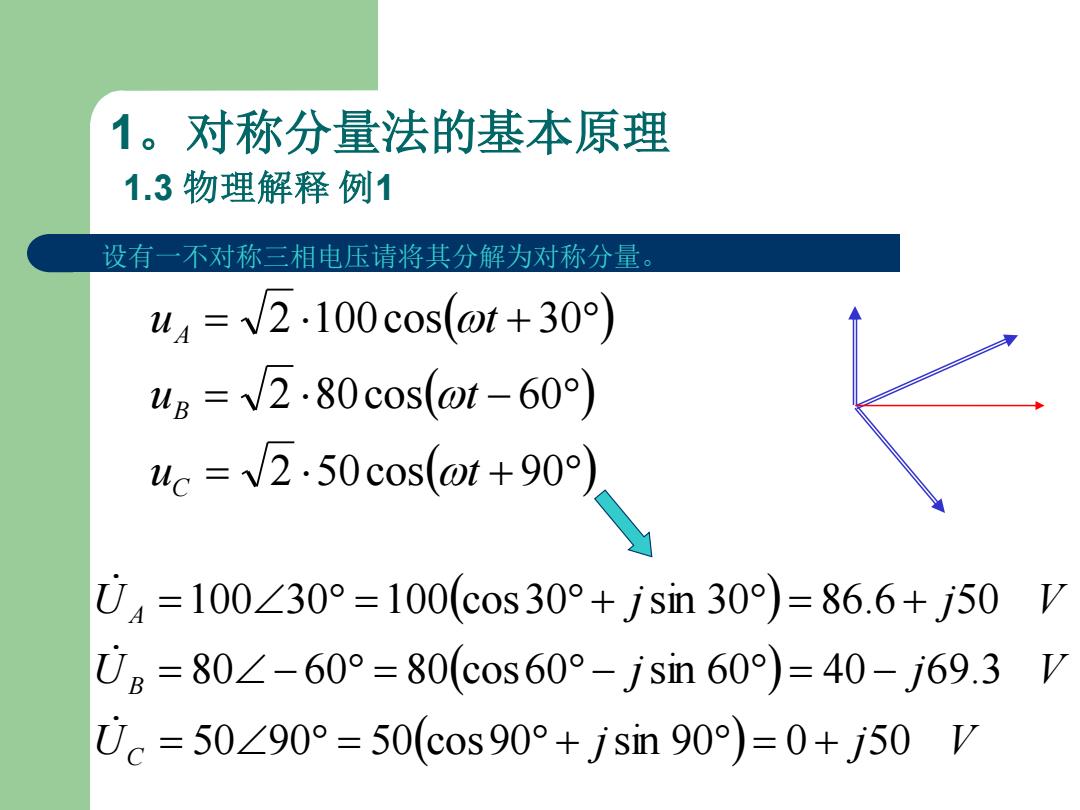
1。对称分量法的基本原理 1.3 物理解释 例1 ( ) ( ) = ( + ) = − = + 2 50cos 90 2 80cos 60 2 100cos 30 u t u t u t C B A ( ) ( ) U ( j ) j V U j j V U j j V C B A 50 90 50 cos90 sin 90 0 50 80 60 80 cos60 sin 60 40 69.3 100 30 100 cos30 sin 30 86.6 50 = = + = + = − = − = − = = + = + 设有一不对称三相电压请将其分解为对称分量

0.=04+a0a+a20c) 1。对称分量法的基本原理 0-=304+a0s+a0c) 1.3物理解释例1 0。=0+0。+0c) 注意每一个 设有一不对称三相电压请将其分解为对称分量。 对称系统又 有abc三个 0=1/3*04+aUB+a2Uc) 分量 =1/3*86.6+j50)+(←支+j9X40-j69.3)+(支-j90+j50) =56.6+31.43V U=1/3*04+a20n+aUc) =1/3*86.6+750)+(--j9X40-j69.3)+(+j号0+j50)) =-12.2+8.33V 0,=3,+0。+0c)=86.6+50+(40-j693)+0+j50)=422+1023
1。对称分量法的基本原理 1.3 物理解释 例 1 ( ) (( ) ( ) ) j V j j j j j U UA UB UC 12.2 8.33 1/ 3* 86.6 50 ( )(40 69.3) (0 50) 1/ 3* 23 21 23 21 2 = − + = + + − − − + − + + − = + + U (UA UB UC ) ((86.6 j50) (40 j69.3) (0 j50)) 42.2 j10.23 V 31 31 0 = + + = + + − + + = + 设有一不对称三相电压请将其分解为对称分量。 ( ) (( ) ( ) ) j V j j j j j U UA UB UC 56.6 31.43 1/ 3* 86.6 50 ( )(40 69.3) (0 50) 1/ 3* 23 21 23 21 2 = + = + + − + − + − − + + = + + = + + = + + + = + + ( ) 31 ( ) 31( ) 31 0 2 2 A B C A B C A B C U U U U U U a U aU U U aU a U - 注意每一个 对称系统又 有abc三个 分量
心.=o+ais+oi。) 1。对称分量法的基本原理 0=204+a20s+a0c) 1.3物理解释例2 0。=0+U+0.) 设有一不对称三相电压请将其分解为对称分量。 14=I∠0° i4=V2.lcos(aot) ip=0 =0 通入火三相对称 绕组,结果怎 ic =0 样? 注意其物,记 住结论理含义 =2
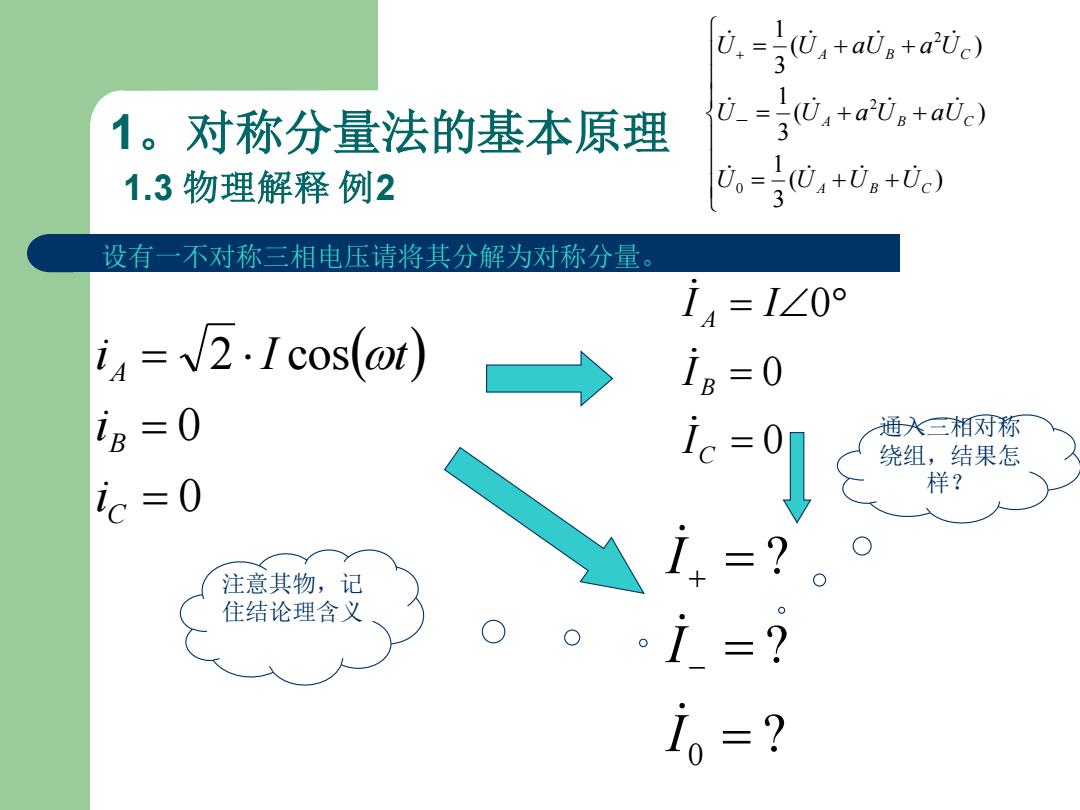
1。对称分量法的基本原理 1.3 物理解释 例2 ( ) 0 0 2 cos = = = C B A i i i I t 0 0 0 = = = C B A I I I I 设有一不对称三相电压请将其分解为对称分量。 注意其物,记 住结论理含义 ? ? ? 0 = = = − + I I I = + + = + + + = + + ( ) 3 1 ( ) 3 1 ( ) 3 1 0 2 2 A B C A B C A B C U U U U U U a U aU U U aU a U - 通入三相对称 绕组,结果怎 样?

1。对称分量法的基本原理 1.3物理解释及算例 结论 (1)正序、负序和零序系统都是对称系统。当求得各个对称分量后, 再把各相的三个分量叠加便得到不对称运行情形。 (2)不同相序可能具有不同的阻抗参数:即存在相应的正序阻抗、 负序阻抗和零序阻抗,其电流流经电机和变压器具有不同物理性 质。 (3)对称分量法根据叠加原理,只适用于线性参数的电路中
1。对称分量法的基本原理 1.3 物理解释及算例 (1)正序、负序和零序系统都是对称系统。当求得各个对称分量后, 再把各相的三个分量叠加便得到不对称运行情形。 (2)不同相序可能具有不同的阻抗参数:即存在相应的正序阻抗、 负序阻抗和零序阻抗,其电流流经电机和变压器具有不同物理性 质。 (3)对称分量法根据叠加原理,只适用于线性参数的电路中。 结论