重庆大学：《电机学》课程教学资源（PPT课件）电机不对称运行

1。对称分量法的基本原理（汤书p258) 1.2不对称与对称系统的转换一一对称分量法 要求解不对称三相系统，就需要将不对称转换为对称系统 转换的方法：对称分量法： 转换的思想：把不对称的三相系统分解为相序分别为正、负、零的三个独 立的对称系统的叠加 三个独立变量+两个相对角度变量 转换的思路： a。假设有独立对称系统U+,U一，Uo,其叠加正构成不对称三相系统； b。 如果能找到这三个对称系统的表达式，则假设成立； c。相应的，不对称的三相系统也就分解城了三个独立的对称系统U+,U一， Uo

1。对称分量法的基本原理(汤书p258) 1.2 不对称与对称系统的转换－－对称分量法 要求解不对称三相系统，就需要将不对称转换为对称系统 转换的方法：对称分量法； 转换的思想：把不对称的三相系统分解为相序分别为正、负、零的三个独 立的对称系统的叠加 转换的思路： a。假设有独立对称系统U+,U－,Uo，其叠加正好构成不对称三相系统； b。如果能够找到这三个对称系统的表达式，则假设成立； c。相应的，不对称的三相系统也就分解成了三个独立的对称系统U+,U－, Uo， 三个独立变量+两个相对角度变量

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 U4=0+0-+00 转换的推导 Un-U +U8+U Uc =Uo:+UE _+Uco U4,心a,Uc构成对称正序系统U U4,0a,Uc构成对称损序系统U Uc构成对称零序系统U

     = + + = + + = + + + − + − + − 0 0 0 C C C C B B B B A A A A U U U U U U U U U U U U             1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法 转 换 的 推 导 U 0 U 0 U 0 U0 U U U U U U U U A B C A B C A B C             ， ， 构成对称零序系统 ， ， 构成对称负序系统 ， ， 构成对称正序系统 − − − － + + + +

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 04,U+,0c,构成对称正序系统0→04=U,U=aU,Uc+=a0 04-,0a-,Uc构成对称负序系统U_→04-=U,0。-=aU,0c-=a0 Uo,Uc构成对称零序系统U。→U0=Uo=Uc0=U。 心，=0：-，+k-伯-0+心 UB=UBs+Up-+Umo-aU.+al_+Uo 0c=0c++Uc+0c0=a0,+a20+0

1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法      → = → = → = − − − − − − − − − + + + + + + + + + + 0 0 0 0 0 0 0 0 2 2 U U U U U U U U U U U U U U U aU U a U U U U U U U U a U U aU A B C A B C A B C A B C A B C A B C                             ， ， 构成对称零序系统 ＝ ＝ ， ， 构成对称负序系统 ， ＝ ， ＝ ， ， 构成对称正序系统 ， ＝ ， ＝ －      = + + + + = + + + + = + + + + + − + − + − + − + − + − 0 2 0 0 2 0 0 0 U U U U aU a U U U U U U a U aU U U U U U U U U C C C C B B B B A A A A                      ＝ ＝ ＝

1。对称分量法的基本原理 1.2不对称与对称系统的转换一一对称分量法 U U A 文立立 U 1 0 , U 3 Z ABC -(U,+aUg+a-Uc) -3心，+a0+ue） =3心，+0a+0)

1。对称分量法的基本原理 1.2 不对称与对称系统的转换－－对称分量法                      =           − + 0 2 2 1 1 1 1 1 U U U a a a a U U U C B A                            =            − + C B A U U U a a a a U U U       1 1 1 1 1 3 1 2 2 0 +−0 Z ABC          = + + = + + + = + + ( ) 3 1 ( ) 3 1 ( ) 3 1 0 2 2 A B C A B C A B C U U U U U U a U aU U U aU a U             － ABC Z+−0

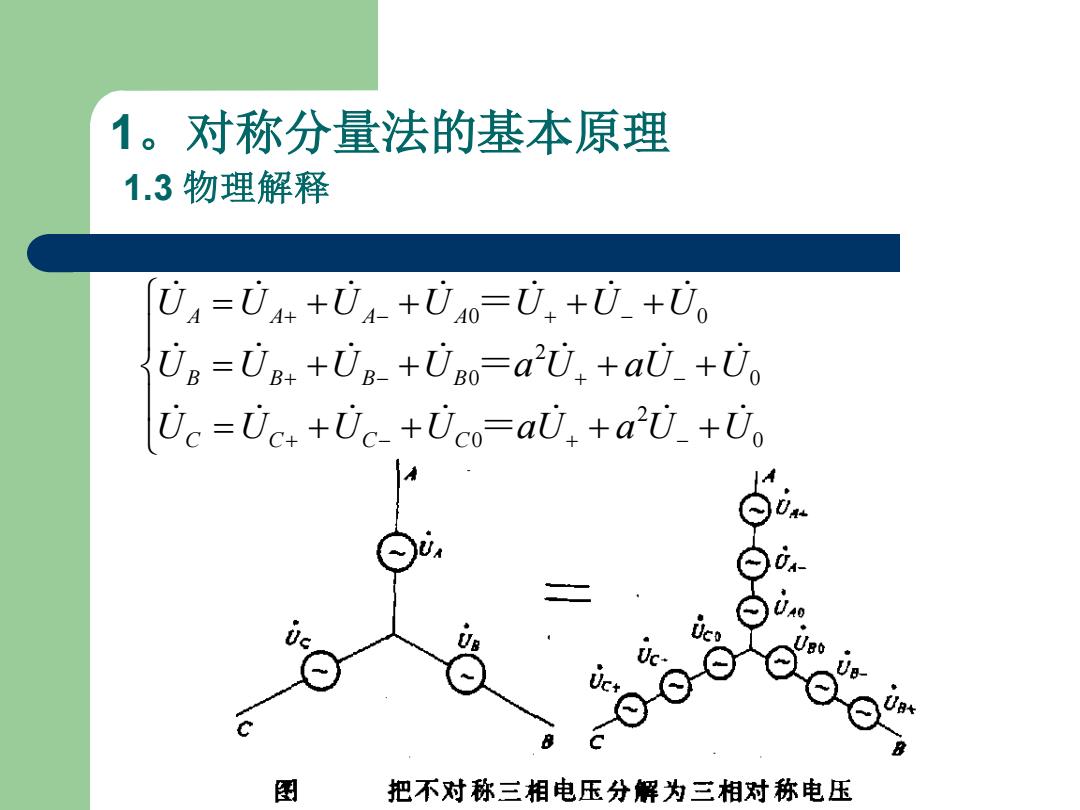
1。对称分量法的基本原理 1.3物理解释 U4=UA4++U4-+U40=U,+U+U。 Ug=Ug:+UB-+Umo-aU:+aU_+Uo Uc=Uc:+Uc-+Uco=al,+aU_+Uo J80 图 把不对称三相电压分解为三相对称电压

1。对称分量法的基本原理 1.3 物理解释      = + + + + = + + + + = + + + + + − + − + − + − + − + − 0 2 0 0 2 0 0 0 U U U U aU a U U U U U U a U aU U U U U U U U U C C C C B B B B A A A A                      ＝ ＝ ＝