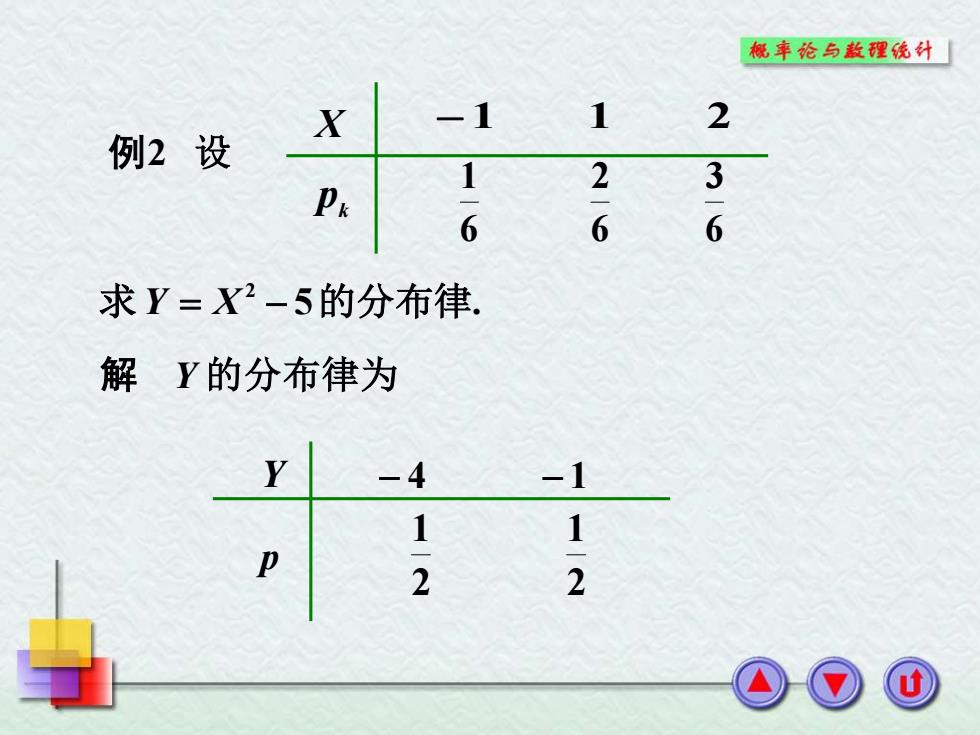
概车纶与款理统外 X 一1 1 2 例2设 3 6 2-6 6 求Y=X-5的分布律. 解Y的分布律为 4 1 1 2 2
Y 的分布律为 Y p − 4 − 1 2 1 2 1 X k p − 1 1 2 6 1 6 2 6 3 例2 设 5 . 求Y = X 2 − 的分布律 解

概率纶与款理统外「 二、连续型随机变量的函数的分布 例3 设随机变量X的概率密度为 Jx(x)= P, 0<x<4, 0,其他. 求随机变量Y=2X+8的概率密度: 解第一步先求Y=2X+8的分布函数F,(y) F,(y)=P{Y≤y}=P{2X+8≤y}
第一步 先求Y=2X+8 的分布函数 F ( y). Y F ( y) P{Y y} Y = = P{2X + 8 y} 解 二、连续型随机变量的函数的分布 2 8 . 0, . , 0 4, ( ) 8 求随机变量 的概率密度 其他 设随机变量 的概率密度为 = + = Y X x x f x X X 例3

概车纶与款理统外 =Px≤'2=dx 第二步由分布函数求概率密度 fy(y)=F,(y) fx(x)dxr =2828
f ( y) F ( y) Y y = f x x y X ( )d 2 8 − − }= 2 8 { − = y P X ) , 2 8 )( 2 8 ( − − = y y fX 第二步 由分布函数求概率密度. [ ( )d ] 2 8 = − − f x x y X