电子科技大学：《信号处理理论与算法》课程教学资源（课件讲稿）第二部分 CH01 随机信号的相关和功率谱分析

相关分析及应用 2w- x1(t) x2( >如果Q=0,则两信号波形完全相等； >如果Q的数值小，表示两个信号波形差 (a)时域波形 )2)时域波形 y(t) y2(t) 别不大，相似； >如果Q的数值大，表示两个信号波形差 A 别大，不相似。 (c)⊙时域波形 (④2①时域波形 1 1 1N2+yiN可 四种波形的相似比较 1 R= Xyi 0 >的数值大，C就小，其意义表示两个信 y④ 号的相似性较好，反之则相似性差。 间 波形相似程度分析 17

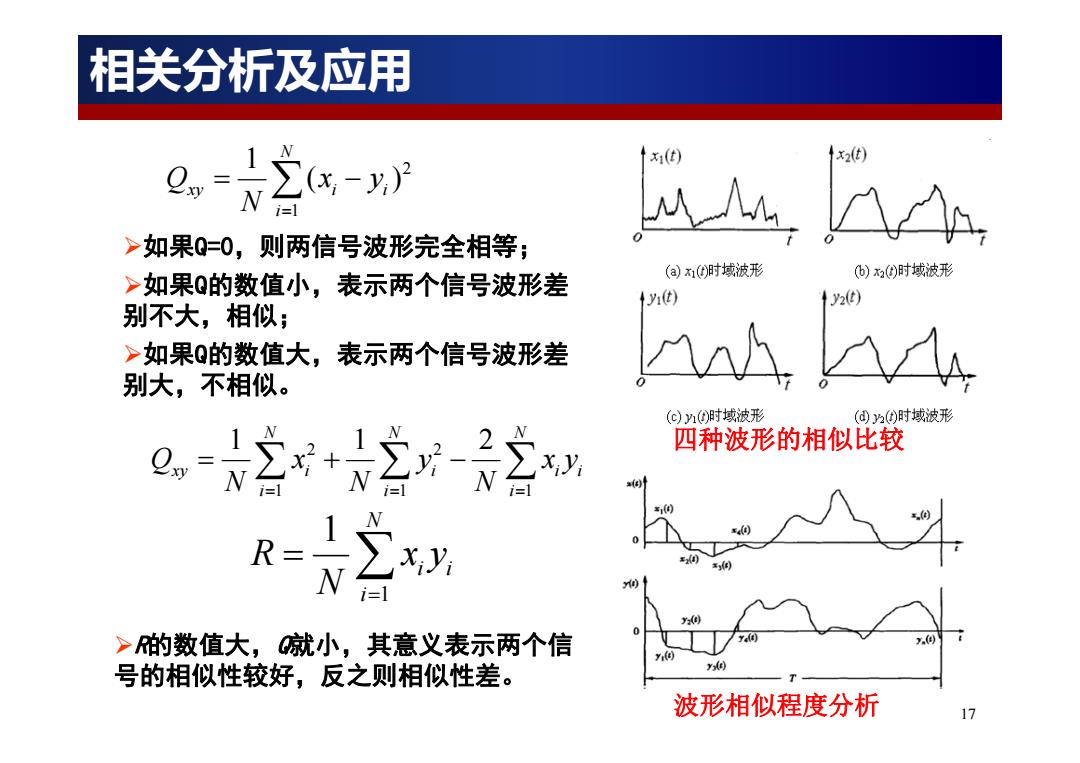
波形相似程度分析 17 四种波形的相似比较 2 1 1 ( ) N xy i i i Q xy N     如果Q=0，则两信号波形完全相等； 如果Q的数值小，表示两个信号波形差 别不大，相似； 如果Q的数值大，表示两个信号波形差 别大，不相似。 2 2 111 112 NNN xy i i ii iii Q x y xy NNN    1 1 N i i i R xy N    R的数值大，Q就小，其意义表示两个信 号的相似性较好，反之则相似性差。 相关分析及应用

相关函数和相关系数 相关函数 随机变量x()和y在不同时刻的乘积平均来描述它们之 间的线性相关程度，称为相关函数，表示为： R..(( 式中，T∈(-o0,o),表示时间位移，或时延，为连续变量，与t 无关。 x(0 Rx(t) 积分器 y() x(t- 18

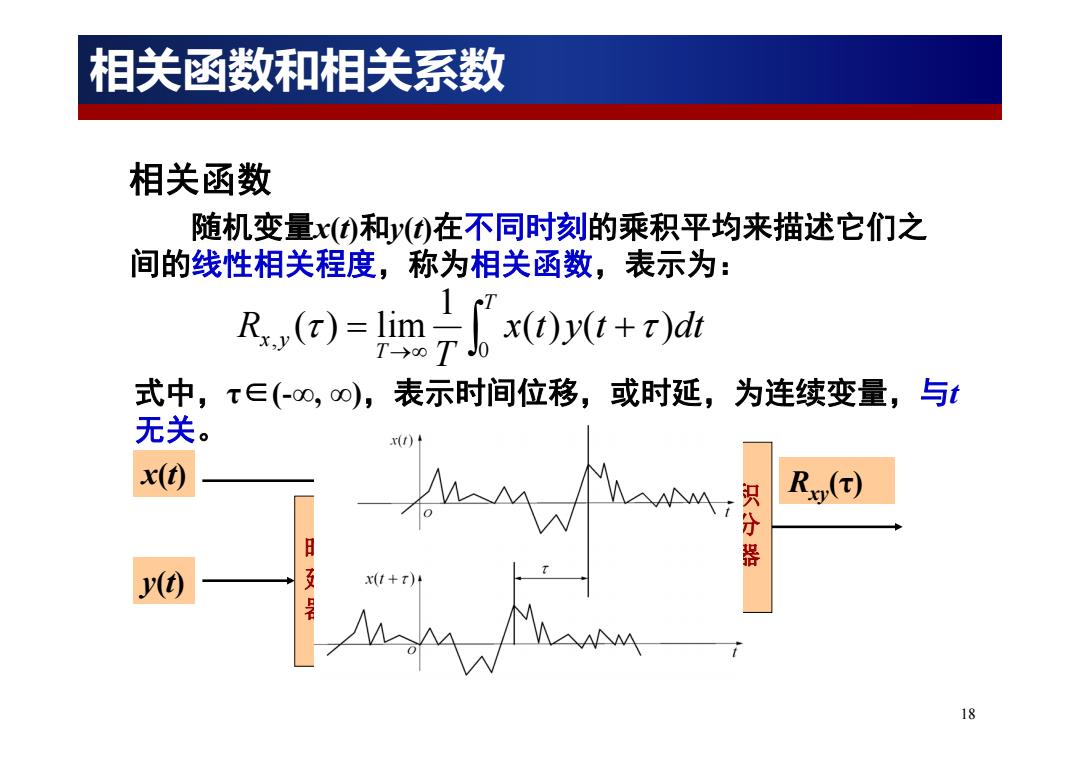
18 随机变量x(t)和y(t)在不同时刻的乘积平均来描述它们之 间的线性相关程度，称为相关函数，表示为： 式中，τ∈(-∞, ∞)，表示时间位移，或时延，为连续变量，与t 无关。     T T x y x t y t dt T R 0 , ( ) ( ) 1 ( ) lim  相关函数 x(t) y(t) 时 延 器 乘 法 器 y(t +τ) x(t)y(t +τ) 积 分 器 Rxy(τ) 相关函数和相关系数

相关系数 >用相关系数表示两个变量x,y之间的相关程度 Elx-4y-4,小 OxOy p1当p=±1时，则随机变量x,y具有理想的线性关系 当Py=0时，两随机变量x,完全不相关 y 000 0 0 0 0 X 0 X X 0 0 X 00 P=1 Py=-1 0≤Pw≤1 =0 19

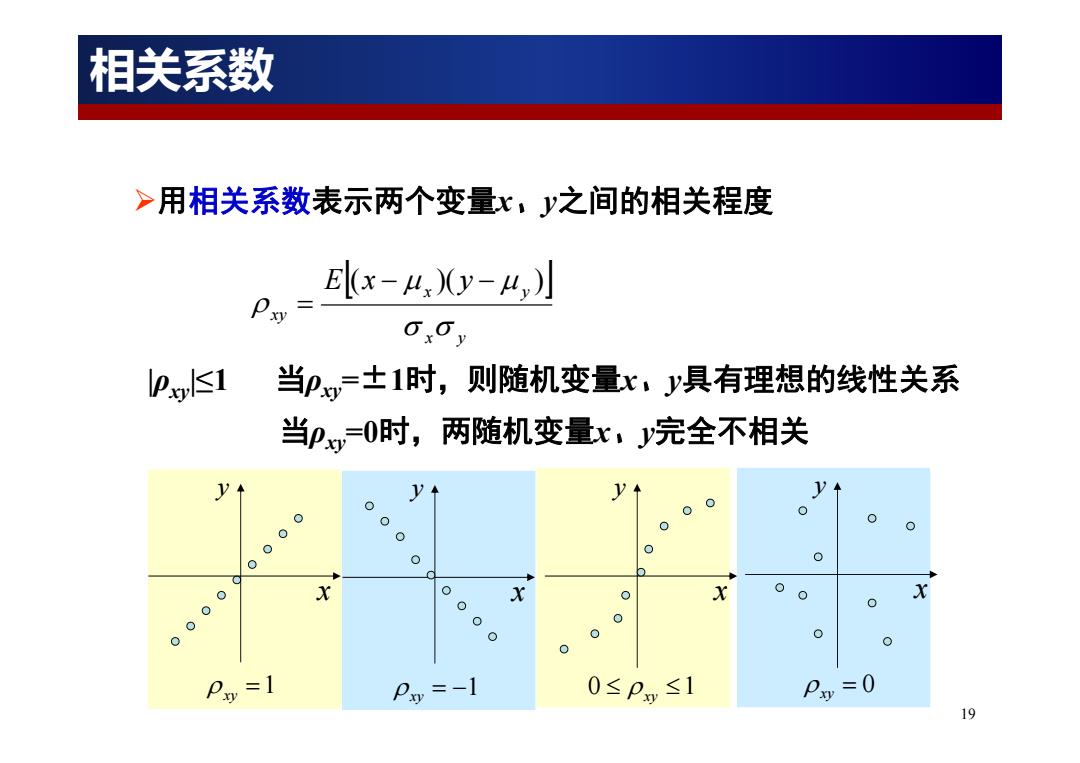
19 用相关系数表示两个变量x、y之间的相关程度   x y x y xy E x y      (  )(  )  |ρxy|≤1 当ρxy=±1时，则随机变量x、y具有理想的线性关系 当ρxy=0时，两随机变量x、y完全不相关 x y  xy 1 x y  1  xy x y 0  1  xy x y  0  xy 相关系数

相关函数和相关系数 >设yt什)是y()时延τ后的样本，对于x()和y(t什T)的相关系数 Px(t)y(t+r)简写为P,() R.()-imx(+d ,-E[x-40-4,)] (2) OxOy m7[x)-4,1e+)-4,1dM ()-HMy (3) 0xOy 00y 20

20 设y(t+τ)是y(t)时延τ后的样本，对于x(t)和y(t+τ)的相关系数  x(t) y(t ) 简写为ρxy(τ) (1) (2) (3) 相关函数和相关系数 0 1 lim [ ( ) ][ ( ) ] ( ) T x y T xy x y x t y t dt T            , 0 1 ( ) lim ( ) ( ) T x y T R x t y t dt T       ( )( ) x y xy x y Ex y             , ( ) x y xy x y R       

相关函数和相关系数 Elx-4y-4,小 (2) 00y >设yt什)是y)时延τ后的样本，对于x()和y(t什)的相关系数 Px(D)y(++) 简写为P() -1x0)-41D0+4,h E(0-4)=m子[x0)-41d P(t)= E00)-4)=m子0)-4,1d OxOy m7t+)-eA,-t+r.+44,h d[=0e+-%=0%=uth* -R,(e)-44,-44,+44]=-丛 00y 21

21   x y T y x x y T x t y t x t y t dt T                  0 ( ) ( ) ( ) ( ) 1 lim                     T TT x y T x T y T x y y t dt T x t dt T x t y t dt T 0 00 ( ) 1 ( ) lim 1 ( ) ( ) lim 1 lim 1         [ ( ) ] 1 x, y y x x y x y x y R                x y x y xy E x y      (  )(  )       T T x y x t y t dt T R 0 , ( ) ( ) 1 ( ) lim       T x T x x t dt T E x t 0 [ ( ) ] 1 ( ( )  ) lim        T y T y y t dt T E y t 0 [ ( ) ] 1 ( ( )  ) lim   设y ( t+τ) 是y ( t)时延 τ后的样本，对于 x ( t) 和y ( t+τ)的相关系数  x(t) y(t ) 简写为 ρxy(τ) (1) (2) x y T x y T xy x t y t dt T               0 [ ( ) ][ ( ) ] 1 lim ( ) x y R x y x y        ( ) , 相关函数和相关系数