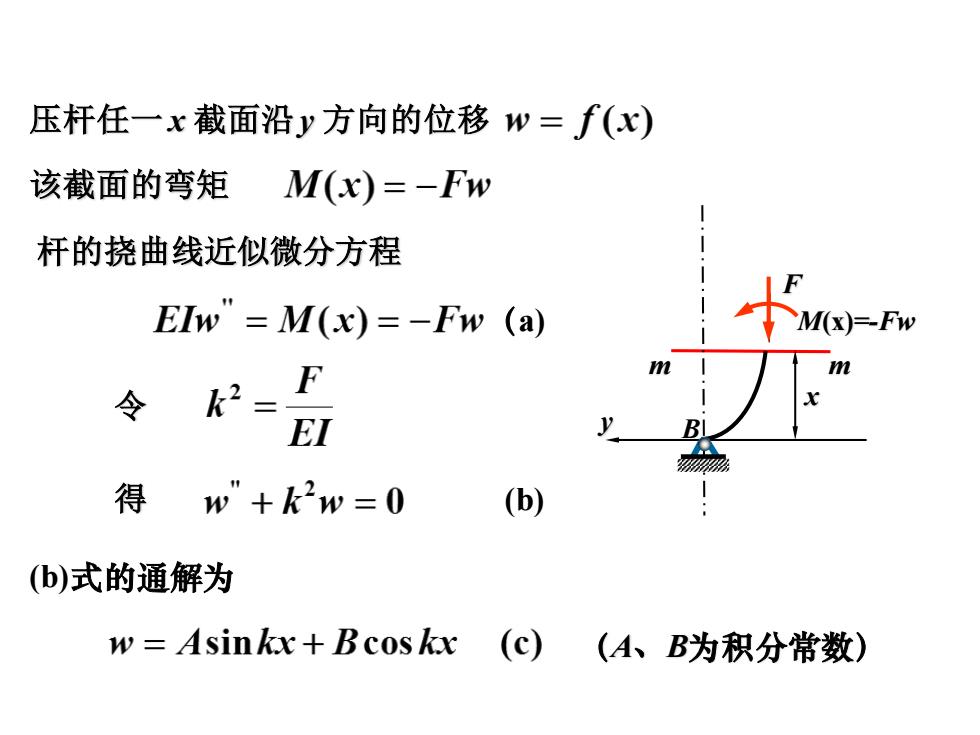
压杆任一x截面沿y方向的位移w=f(x) 该截面的弯矩 M(x)=-Fw 杆的挠曲线近似微分方程 EIw"=M(x)=-Fw (a) Mx=Fw F 令 k2= EI B % 得 w”+k2w=0 (b) (b)式的通解为 w=Asinkx+Bcoskx (c) (A、B为积分常数)
该截面的弯矩 杆的挠曲线近似微分方程 压杆任一 x 截面沿 y 方向的位移 (a) 令 (b)式的通解为 (A、B为积分常数) 得 (b) m m x y B F M(x)=-Fw
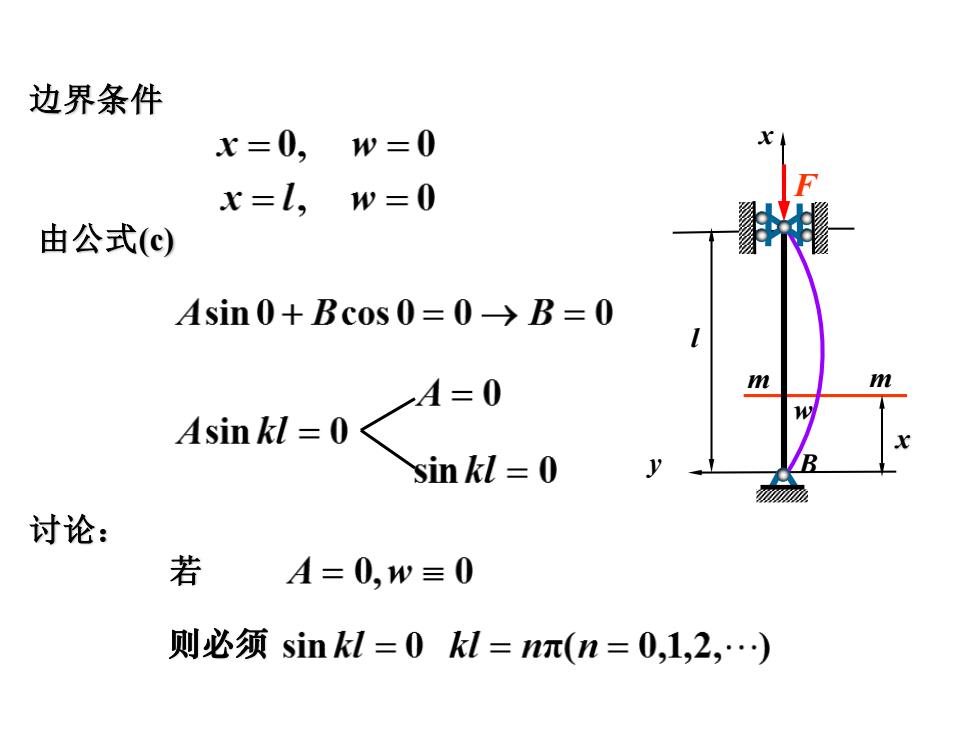
边界条件 x=0, w=0 x=l, w=0 由公式(c) Asin0+Bcos0=0→B=0 A=0 m Asin kl =0 sin kl 0 讨论: 若 A=0,w≡0 则必须sin kl=0kl=nπ(n=0,1,2,)
边界条件 由公式(c) 讨论: 若 m x m wB x y l F 则必须

k2= F kl=nπ(n=0,1,2,) EI F- n'x2EI (n=0,1,2,.) 12 令n=l,得F=元BI 2 这就是两端铰支等截面细长受压直杆临 界力的计算公式(欧拉公式) 6 挠曲线方程为w= kisin ke sin- 2 当kl=π时,w=δsin 1 挠曲线为半波正弦曲线
这就是两端铰支等截面细长受压直杆临 界力的计算公式(欧拉公式). 令 n = 1, 得 当 时, 挠曲线方程为 挠曲线为半波正弦曲线. m x m w B x y l F
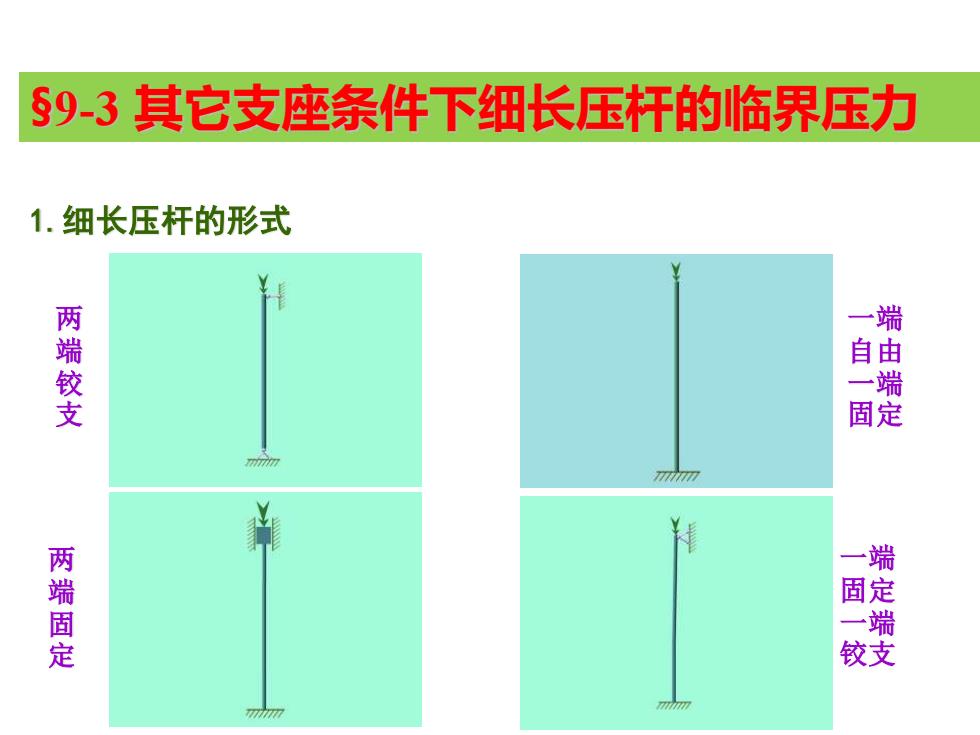
§9-3其它支座条件下细长压杆的临界压力 1.细长压杆的形式 两端较支 自 由 固定 两端固定 端 固一 铰支
1.细长压杆的形式 两 端 铰 支 一端 自由 一端 固定 一端 固定 一端 铰支 两 端 固 定 §9-3 其它支座条件下细长压杆的临界压力
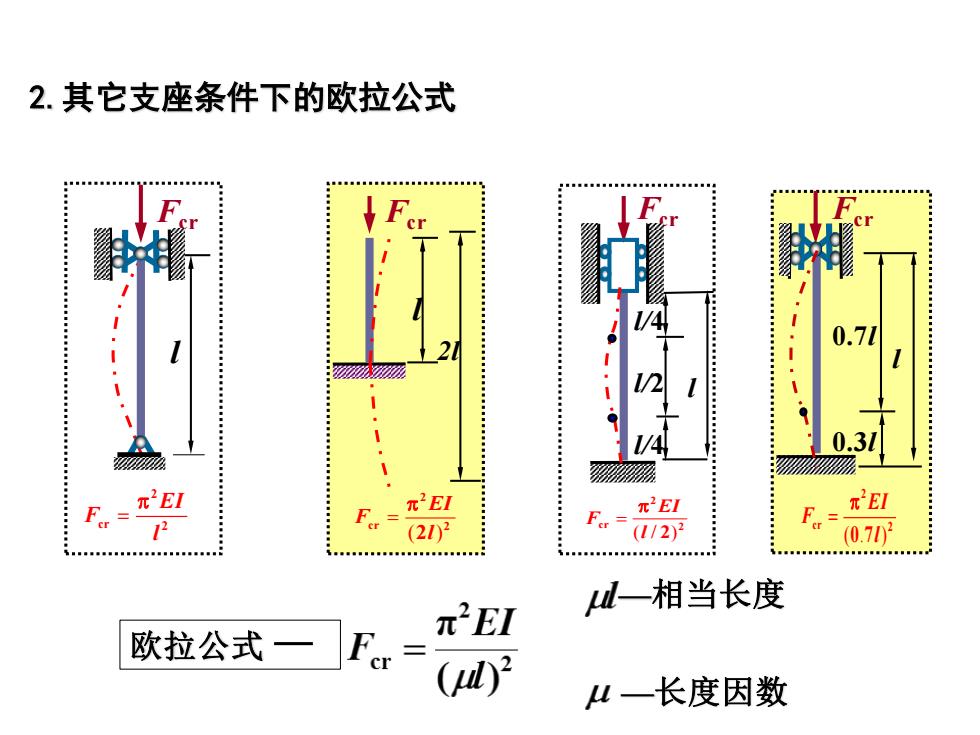
2.其它支座条件下的欧拉公式 71 0.3l π2EI n'El π2E1 π'EI 12 = er (21)2 (112)2 f- 0.702 l一相当长度 π2E1 欧拉公式一 (l)2 4一长度因数
2.其它支座条件下的欧拉公式 l Fcr 2l ( ) = 2 cr 2 2 EI F l Fcr l 0.3l 0.7l ( . ) = 2 cr 2 0 7 EI F l Fcr l = 2 cr 2 EI F l —长度因数 —相当长度 欧拉公式 l Fcr l/4 l/4 l/2 ( / ) = 2 cr 2 2 EI F l l