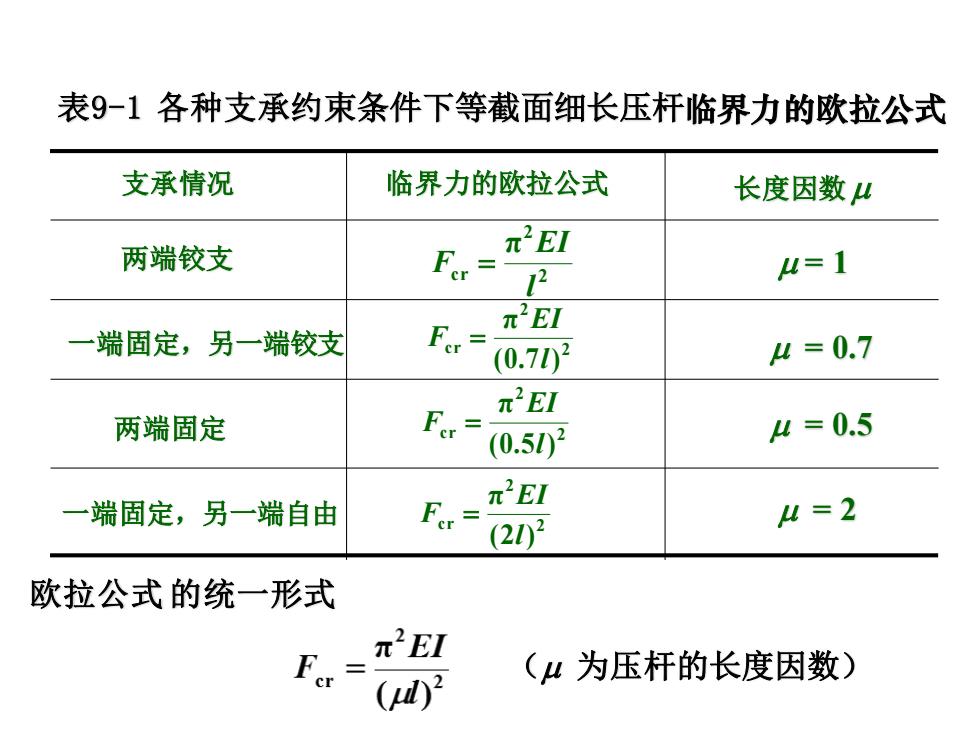
表9-1各种支承约束条件下等截面细长压杆临界力的欧拉公式 支承情况 临界力的欧拉公式 长度因数4 两端铰支 元2EI 2 A=1 一端固定,另一端铰支 F=n (0.702 4=0.7 π2E1 两端固定 (0.502 4=0.5 一端固定,另一端自由 元2EI (202 A=2 欧拉公式的统一形式 π2EI (山为压杆的长度因数) ()2
两端铰支 一端固定,另一端铰支 两端固定 一端固定,另一端自由 表9-1 各种支承约束条件下等截面细长压杆临界力的欧拉公式 支承情况 临界力的欧拉公式 长度因数 = 1 = 0.7 = 0.5 = 2 欧拉公式 的统一形式 ( 为压杆的长度因数) 2 2 cr π l EI F = 2 2 cr (0.7 ) π l EI F = 2 2 cr (0.5 ) π l EI F = 2 2 cr (2 ) π l EI F =

π2E1 4为长度因数 F ul为相当长度 5.讨论 (1)相当长度ul的物理意义 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当长 度μl. 4是各种支承条件下,细长压杆失稳时,挠曲线中相当于 半波正弦曲线的一段长度
5.讨论 为长度因数 l 为相当长度 (1)相当长度 l 的物理意义 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当长 度 l . l是各种支承条件下,细长压杆失稳时,挠曲线中相当于 半波正弦曲线的一段长度