上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.3-Relative Constraint

Definition of the constraint Inertial frame O-e B Body-fixed frame of B C, 9,=,) P 9s=(9 is given Body-fixed frame of B, C,-e; 4=9,)厂 5=y)is given Define vector h=0p=9-=时+9--s” h=r+As-r-As The distance between P and Q is constant:c h.h-c2=0 rd(i.i)=hh-c2=0

• Definition of the constraint Bj y  x  O j x  j y  Cj j r  P Q j r Q j s e  Inertial frame O  C j j e  Body-fixed frame of Bj    T T j j  j q  r Q j s   Q T j Q j Q j s  x  y  is given P i s   T T i i i q  r P i s   T P i P i P i s  x  y  is given C i i e  Body-fixed frame of Bi  i x  i y  Ci Bi ir Q h  P ir Define vector h  QP  P i Q j r r     P i i Q j j r s r s         P i i i Q j j j h  r  A s  r  As 0 2 h  h  c     The distance between P and Q is constant：c 0 T 2  h h  c  rd (i, j)  Bj y  x  O j x  j y  Cj j r  P Q j r Q j s P i s i x  i y  Ci Bi ir Q h  P ir

Φai,)=hTh-c2=0 B h=r+A s'o-r-As P Number of constraint equation:s- 4,=9,4,=p, P q=g）=tg9,rp,） O x Degrees of freedom:=5 Parameters of the constraint i,j,s=(,s9=(°y9,c

 0 P i i i Q j j j h  r  A s  r  As ( , ) T 2 c rd i j Φ  h h  s  1 Degrees of freedom:   5 Number of constraint equation:   T T i i i q  r Parameters of the constraint   T T j j  j q  r     T T T T T T i j i i j  j q  q q  r r i j x y  x y  c Q j Q j Q j P i P i P i , , , , T T s    s    Bj y  x  O j x  j y  Cj j r  P Q j r Q j s P i s i x  i y  Ci Bi ir Q h  P ir

Φdi)=hTh-c2=0 h=ro-r ro=r+A s'o r=r+As. Time derivative of the constraint equation leads to Φai,)=hTh+hh=2hTi=0 h=2-”9=i+RA,0,=月+B,yp, =+RA,s0,=+B,s0 本u》=2h(G+Bsp,--B,s0,) -bha6l-26]-0 D=【2h-2hBsr本，D=2n2hBs9] vd》=-Dyd》=0

Time derivative of the constraint equation leads to • 速度约束方程 P i Q j h r r    0 ( , ) 2   c  rd i j Φ h h T 2 0 ( , ) T T T Φ  h h  h h  h h      rd i j P i Q j h  r  r Q j j j Q j r  r  A s P i i i P ir  r  A s j Q j j j j Q j j j Q r j  r  RA s   r  B s  i P i i i i P i i i P r i  r  RA s   r  B s   i P j i i i Q j j j rd i j     Φ  h r  B s  r  B s ( , ) T 2 2 2   2 2  0 T T T T                   i P i i i j Q j j j      r h h B s r h h B s   P i i rd i j i Φ h h B s q     ( , ) T T 2 2   Q j j rd i j j Φ h h B s q   ( , ) T T 2 2 0 ( , ) ( , )    rd i j t rd i j v Φ

prd(i))=hTh+hTh=2hh=0 h=ro-r ro=r+A so r=r+As i=9-9=i+RA,0,=+B,s0 =+RAs0,=产+B,s0, Time derivative of the velocity constraint equation leads to rd(i.))=2hTh+2hh h=9-”9=书+R4,s0,+RA,s90=-A,9+Bs9, =i+RAs+RAs =-As+Bs 6n-w2al质}r-28看 +2hih-2hTA,syp+2h'As2=Φ，awi-yaD=0 y=-2hh+2h(As-As2)

P i Q j h r r    2 0 ( , ) T T T Φ  h h  h h  h h      rd i j Φ h h h h  T  T  ( , )  2  2 rd i j P i Q j h  r  r Q j j j Q j r  r  A s P i i i P ir  r  A s j Q j j j j Q j j j Q r j  r  RA s   r  B s  i P i i i i P i i i P r i  r  RA s   r  B s  Time derivative of the velocity constraint equation leads to P i Q j h r r    j Q j j j Q j j j j Q j j j Q j j j Q j       r  r  RA s  RA s  r  A s  B s 2 i P i i i P i i i i P i i i P i i i P i       r  r  RA s  RA s  r  A s  B s 2     T T 2 T 2 ( , ) T T T T 2 2 2 2 2 2 2 i P j i i Q j j i P i i i j Q j j j rd i j              h h h A s h A s r h h B s r Φ h h B s                        0 ( , ) ( , )    rd i j rd i j Φ q  q    ( , ) T T 2 2 2 2 i P j i i Q j j rd i j        h h  h A s  A s

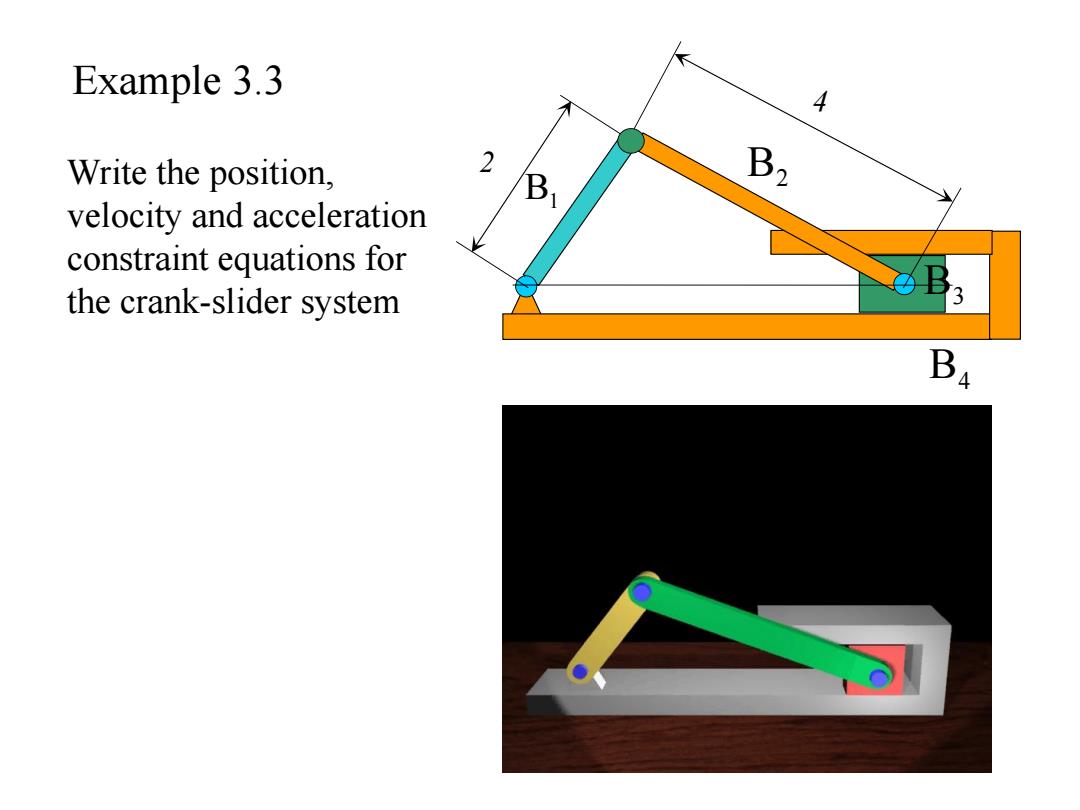
Example 3.3 4 Write the position, 2 B2 velocity and acceleration constraint equations for the crank-slider system 3 Ba

W 2 rite the position, velocity and acceleration constraint equations for the crank-slider system 4 B1 B2 B3 B4 Example 3.3