上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.4-Gears

3.4 Gears and cam-followers 3.4.1 Gears Gear teeth on the periphery of the gears cause pitch circles to roll relative to each other without slip

3.4 Gears and cam-followers 3.4.1 Gears Gear teeth on the periphery of the gears cause pitch circles to roll relative to each other without slip

3.4.1 Gears 1.Outer meshing gear The arc lengths DO,and DO are equal. ↑9 1=0,Q,and Ocoincide a,R,=a R O,and are fixed points on y B;and Bi,0,e,are constant x+0=p+8 a,=4+0-0 R,(,+0,)+R+0)Rπ C%=-(9+0-0-π) R+R x,+8,+4=B+π am明一心1用一r收-=0-8 u Ru w-rk-r小m--0 Two constraint Φ》=(-y(G-）-(R+R,}=0 equations

Qi and Qj are fixed points on Bi and Bj,  j  j  j    3.4.1 Gears The arc lengths DQi and DQj are equal. t = 0, Qi and Qj coincide  (    )             j j j i i i   sin   cos   0 ( , )           P i P j P i P j P i P j T g i j u r r  x x  y y i j j i i j  D Qi Qj u  Pj u Pi       0 ( , ) 2     i  j  P i P j T P i P j rd i j  r r r r R R     i j i i i j j j j R R R R R              Two constraint equations x  y  i x  i y  j x  j y  i  j , are constant i   i i iRi   jRj u PiPj //  u  PiPj      0  P i P j T u r r u  Ru           sin cos u 1. Outer meshing gear

s》=ur(-）=-sine6-x）+cos6y-y）=0 R(,+0,)+R,,+日，-Rπ R,+R,, R+R R+R -[-l-8a. (Rg+R,) R+R 》=(-2）+w6-） R+BsB)=0 R,+R a”-w-ra y8)=0 eai-rg

  sin   cos   0 ( , )          P i P j P i P j P i P j T g i j  u r r  x x  y y Since          0 ( , )                    i P j i i i P j j j T i j i i j j P i P j T P i P j T P i P j T g i j R R R R                u r B s r B s u r r u r r u r r   i j i i j j R R R R                               u u u u u                sin cos , cos sin , sin cos     i j i i i j j j j R R R R R             i j i i j j R R R R          The velocity equation is The Jacobians of the constraint with respect to qi and qj are                i j P i i P j P T i i T T g i j R R R i u u B s u r r q ( , )               i j P j i P j P T j j T T g i j R R R j u u B s u r r q ( , )   0 g (i, j) v

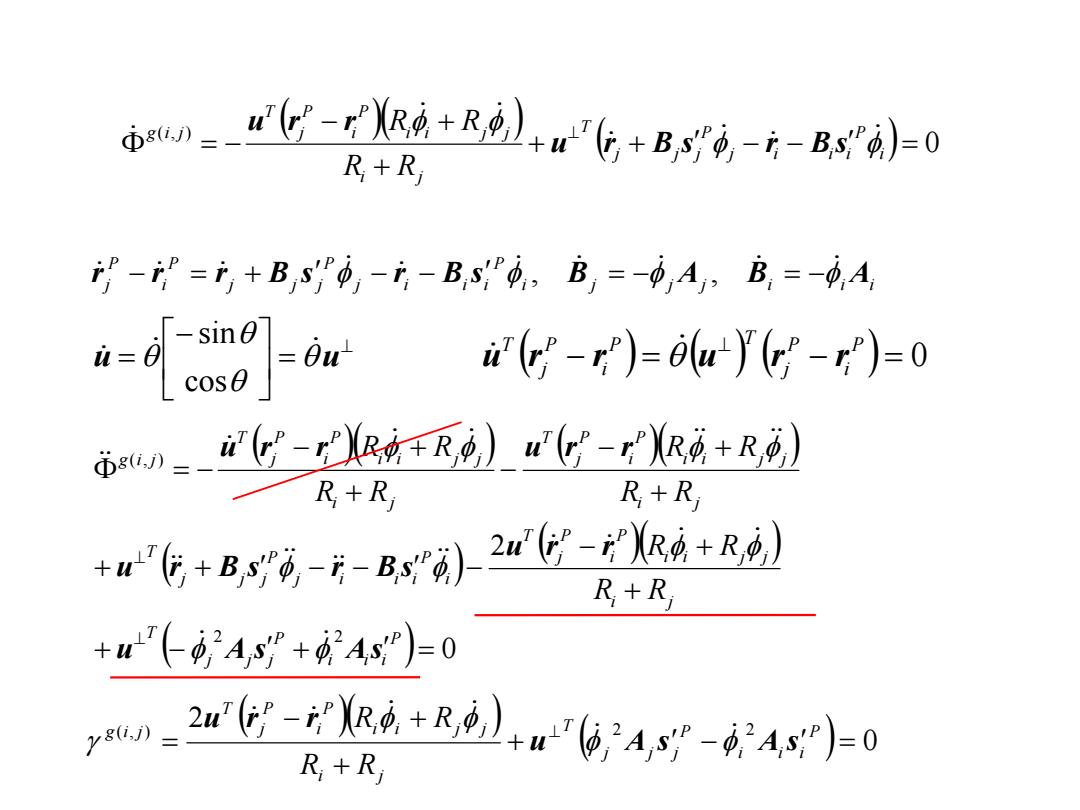
W-R4+R)+r'6+B,s4-i-Bs”)=0 R+R -=i,+B功，-片-Bs4,B,=-中，A,B=-4A4 a=8]-加-）=6-y-）=0 un=-化-转年R）w6-k有+R⊙) R+Rj R+R +n'呢+B,y有-日-Bs)-2m6-A+R》 R+R +u（As+2AsP）=0 2m-R4+R）+u'6,24,s-2As）=0 R+R

     0 ( , )               i P j i i i P j j j T i j i i j j P i P j T g i j R R R R            u r B s r B s u r r Differentiating the velocity equation              0 2 2 2 ( , )                             P i i i P j j j T i j i i j j P i P j T i P j i i i P j j j T i j i i j j P i P j T i j i i j j P i P j T g i j R R R R R R R R R R R R u A s As u r r u r B s r B s u r r u r r                                0 2 ( , ) 2 2           P i i i P j j j T i j i i j j P i P j T g i j R R R R u A s A s u r r            And using i j j j i i i P j i i i P j j j P i P r j  r  r  B s    r  B s   , B    A , B    A        u   u       cos sin           0  P i P j T P i P j T u r r  u r r  

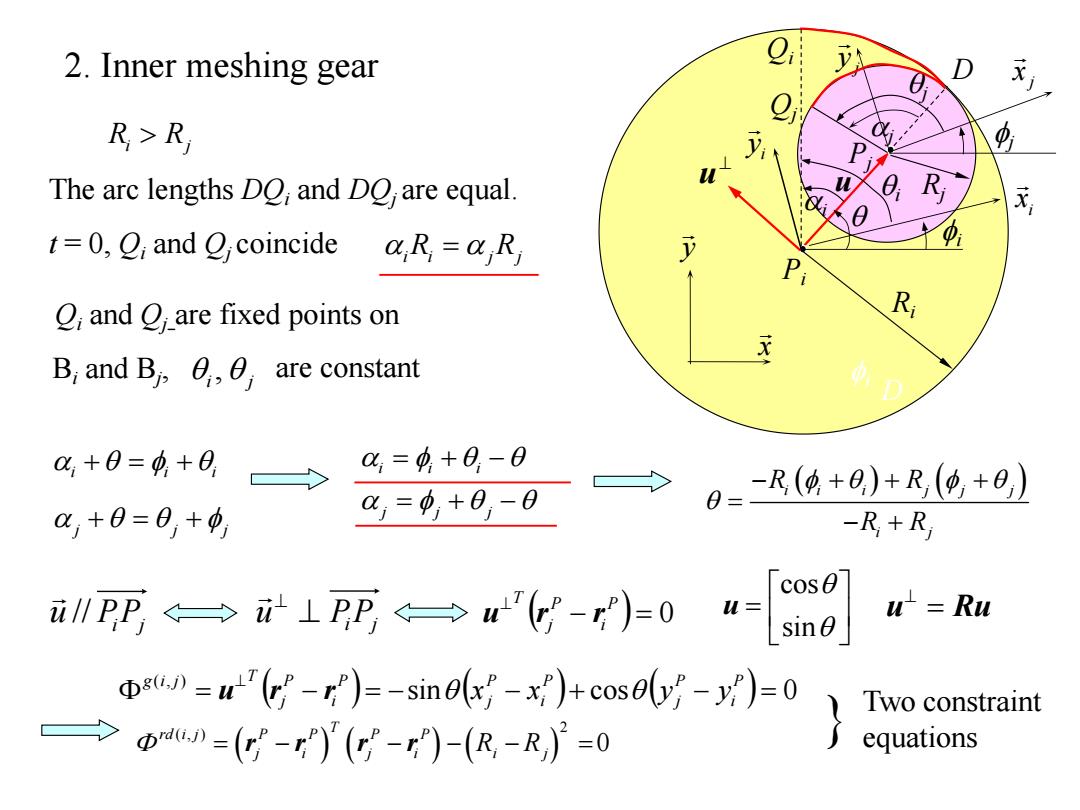
2.Inner meshing gear e. R>R The arc lengths DO;and DO,are equal. t=0,O;and coincide &R=&,R O;and Oare fixed points on Ri B;and Bi,0,,are constant a,+0=+8, %=4+0-0 -R(+0)+R(,+0,) ,+B=日，+9 %,=中，+8，-0 -R+R 吧一i1两一心-小-0[调 u=Ru n=r'6--m心-小-g)=0} Two constraint D》=(g-）Y(-)-(R,-R,)=0 equations

Qi and Qj are fixed points on Bi and Bj,  j    j   j The arc lengths DQi and DQj are equal. t = 0, Qi and Qj coincide i i i j j j                 sin   cos   0 ( , )           P i P j P i P j P i P j T g i j u r r  x x  y y i j i j j i  D Qi Qj u  u Pi Pj       2 ( , ) 0 T rd i j P P P P   rj  ri rj  ri  Ri  Rj  i  i i j  j j i j R R R R              Two constraint equations x  y  i x  i y  j x  j y  i  j , are constant i   i i iRi   jRj u PiPj //  u  PiPj      0  P i P j T u r r u  Ru           sin cos u 2. Inner meshing gear D i Ri  Rj Rj Ri