上海交通大学：《力学仿生——启示与探索》课程教学资源（讲课讲稿）二参数温度模型

二参数温度模型的参数识别与实验验证 目录 1.1DQ200改进的温度模型的推导. 1 1.2DQ200关于模型的假设 .2 1.3DQ200温度模型参数辨识 6 1.3.1参数辨识方法 6 1.3.2在MATLAB中实现最小二乘法参数辨识 1 1.3.3模型1参数辨识结果. 1.3.4模型1的实验验证结果 8 1.3.5模型2参数辨识结果… 10 1.3.6模型2的实验验证结果.… 10 1.3.7原有的二参数温度模型的参数识别 .12 1.3.8原有的二参数温度模型的实验验证 .13 1.4DCT250改进的温度模型参数辨识… .18 1.4.1模型3参数识别结果. 23 1.4.2模型3试验验证结果 23 1.4.3模型4参数识别结果 26 1.4.4模型4实验验证结果 26 1.4.5相同环境温度下滑摩功率与k,k2的关系 29 1.4.6环境温度为26℃参数识别结果… 30 1.4.7环境温度为26℃实验验证结果.… .31 1.4.8环境温度为28℃参数识别结果. 32 1.4.9环境温度为28℃实验验证结果 32 1.4.10四参数温度模型假设… .33 1.4.11四参数温度模型参数识别. .34 1.4.12四参数温度模型实验验证. .34 1.1DQ200改进的温度模型的推导 原有的二参数温度模型： 7- -=kF0o0-k(T0-T.) \MERGEFORMAT (1) △f 上式中为离合器压盘半径，处的温度，F为摩擦界面的正压力，T。为环境空气温度，⊙ 为摩擦界面的转速差。k,为温升系数，k2为散热系数。 其中温升系数k1,和散热系数k,的值均为未知量，若利用该温度模型预测离合器温度 必须先辨识k,k,的值。利用实验数据对不同的工况下的k,k,值进行辨识，发现k1,k2 的值与滑摩功率的大小直接相关。可假设k1,k2与P为线性相关或者指数相关，并分别用

二参数温度模型的参数识别与实验验证 目录 1.1DQ200 改进的温度模型的推导........................................................................................... 1 1.2DQ200 关于模型的假设....................................................................................................... 2 1.3DQ200 温度模型参数辨识................................................................................................... 6 1.3.1 参数辨识方法........................................................................................................... 6 1.3.2 在 MATLAB 中实现最小二乘法参数辨识............................................................... 7 1.3.3 模型 1 参数辨识结果............................................................................................... 8 1.3.4 模型 1 的实验验证结果........................................................................................... 8 1.3.5 模型 2 参数辨识结果............................................................................................. 10 1.3.6 模型 2 的实验验证结果........................................................................................ 10 1.3.7 原有的二参数温度模型的参数识别..................................................................... 12 1.3.8 原有的二参数温度模型的实验验证..................................................................... 13 1.4DCT250 改进的温度模型参数辨识....................................................................................18 1.4.1 模型 3 参数识别结果............................................................................................. 23 1.4.2 模型 3 试验验证结果............................................................................................. 23 1.4.3 模型 4 参数识别结果............................................................................................. 26 1.4.4 模型 4 实验验证结果............................................................................................. 26 1.4.5 相同环境温度下滑摩功率与 1 2 k , k 的关系........................................................... 29 1.4.6 环境温度为 26℃参数识别结果............................................................................ 30 1.4.7 环境温度为 26℃实验验证结果............................................................................ 31 1.4.8 环境温度为 28℃参数识别结果............................................................................ 32 1.4.9 环境温度为 28℃实验验证结果............................................................................ 32 1.4.10 四参数温度模型假设........................................................................................... 33 1.4.11 四参数温度模型参数识别................................................................................... 34 1.4.12 四参数温度模型实验验证................................................................................... 34 1.1DQ200 改进的温度模型的推导 原有的二参数温度模型：             i+1 i 1 2 n n i i i n T T k F k T T t        \* MERGEFORMAT (1) 上式中 i Tn 为离合器压盘半径 r 处的温度，F 为摩擦界面的正压力，T  为环境空气温度， 为摩擦界面的转速差。 k 1 为温升系数， k 2 为散热系数。 其中温升系数 k 1 ，和散热系数 k 2 的值均为未知量，若利用该温度模型预测离合器温度 必须先辨识 k 1 ，k 2 的值。利用实验数据对不同的工况下的 k 1 ，k 2 值进行辨识，发现 k 1 ，k 2 的值与滑摩功率的大小直接相关。可假设 k 1 ，k 2 与 P 为线性相关或者指数相关，并分别用

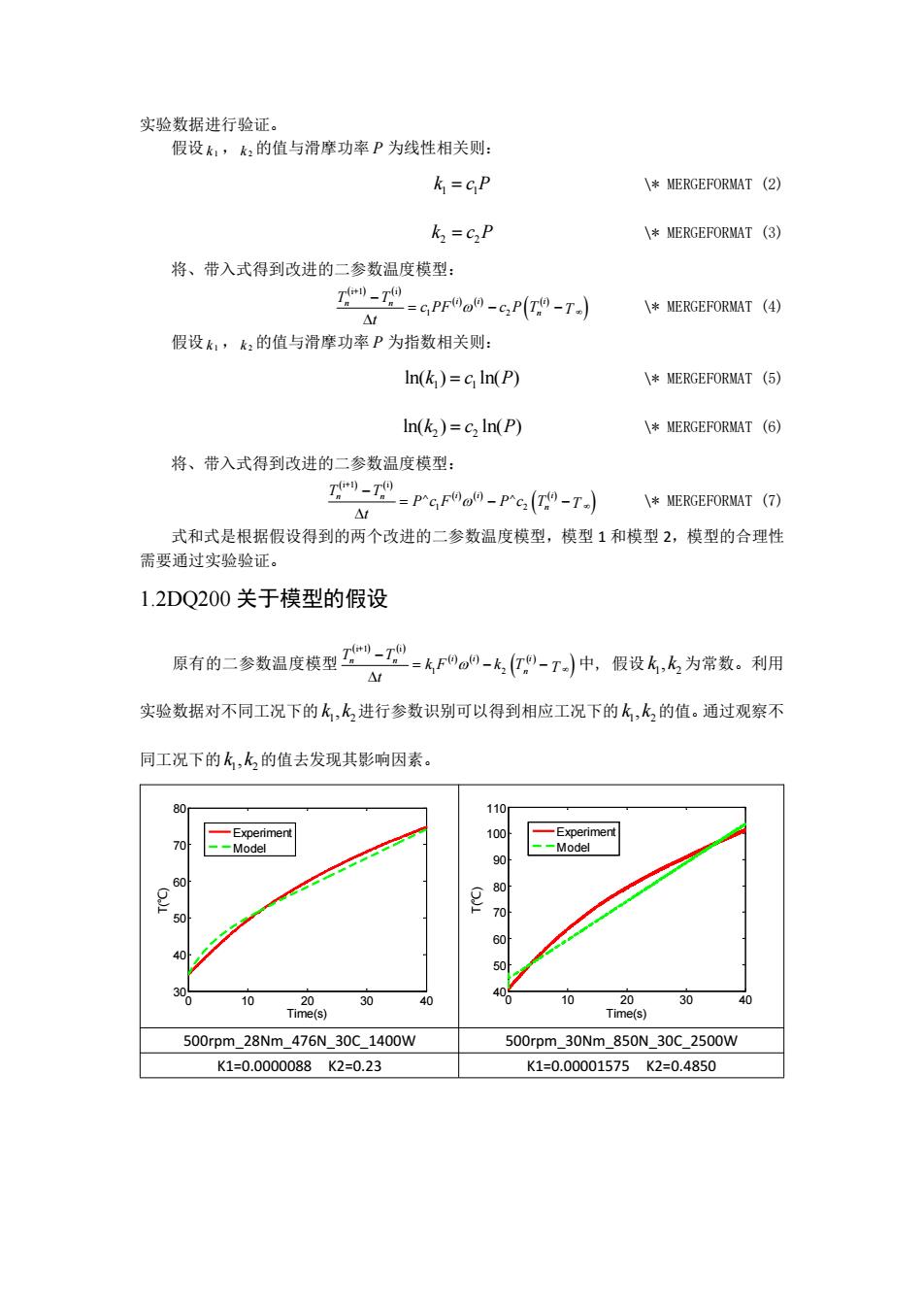
实验数据进行验证。 假设k,k2的值与滑摩功率P为线性相关则： k=cP \MERGEFORMAT (2) k,=C,P \MERGEFORMAT (3) 将、带入式得到改进的二参数温度模型： -70 =cPF0o0-c,P(T9-T） \MERGEFORMAT (4) △t 假设k1,k2的值与滑摩功率P为指数相关则： In(k )=c In(P) \MERGEFORMAT (5) In(k)=c2 In(P) \MERGEFORMAT (6) 将、带入式得到改进的二参数温度模型： 1-TPcFO00-P"c:(T-T) \MERGEFORMAT (7) △t 式和式是根据假设得到的两个改进的二参数温度模型，模型1和模型2，模型的合理性 需要通过实验验证。 1.2DQ200关于模型的假设 原有的二参数温度模型：空-ko-.,的-T中，假设么，k为常数。利用 △ 实验数据对不同工况下的k,k进行参数识别可以得到相应工况下的k,k,的值。通过观察不 同工况下的k,k的值去发现其影响因素。 % 110 -Experiment 100 -Experiment 70 --Model --Model 90 60 g 80 % % SO 0 10 20 30 40 00 10 20 30 40 Time(s) Time(s) 500rpm_28Nm_476N_30C1400W 500rpm_30Nm_850N_30C_2500W K1=0.0000088K2=0.23 K1=0.00001575K2=0.4850

实验数据进行验证。 假设 k 1 ，k 2 的值与滑摩功率 P 为线性相关则： 1 1 k  c P \* MERGEFORMAT (2) 2 2 k  c P \* MERGEFORMAT (3) 将、带入式得到改进的二参数温度模型：             i+1 i 1 2 n n i i i n T T c PF c P T T t        \* MERGEFORMAT (4) 假设 k 1 ，k 2 的值与滑摩功率 P 为指数相关则： 1 1 ln(k )  c ln(P) \* MERGEFORMAT (5) 2 2 ln(k )  c ln(P) \* MERGEFORMAT (6) 将、带入式得到改进的二参数温度模型：             i+1 i 1 2 n n i i i n T T P c F P c T T t          \* MERGEFORMAT (7) 式和式是根据假设得到的两个改进的二参数温度模型，模型 1 和模型 2，模型的合理性 需要通过实验验证。 1.2DQ200 关于模型的假设 原有的二参数温度模型             i+1 i 1 2 n n i i i n T T k F k T T t        中, 假设 1 2 k ,k 为常数。利用 实验数据对不同工况下的 1 2 k ,k 进行参数识别可以得到相应工况下的 1 2 k ,k 的值。通过观察不 同工况下的 1 2 k ,k 的值去发现其影响因素。 0 10 20 30 40 30 40 50 60 70 80 Time(s) T(℃) Experiment Model 0 10 20 30 40 40 50 60 70 80 90 100 110 Time(s) T(℃) Experiment Model 500rpm_28Nm_476N_30C_1400W 500rpm_30Nm_850N_30C_2500W K1=0.0000088 K2=0.23 K1=0.00001575 K2=0.4850

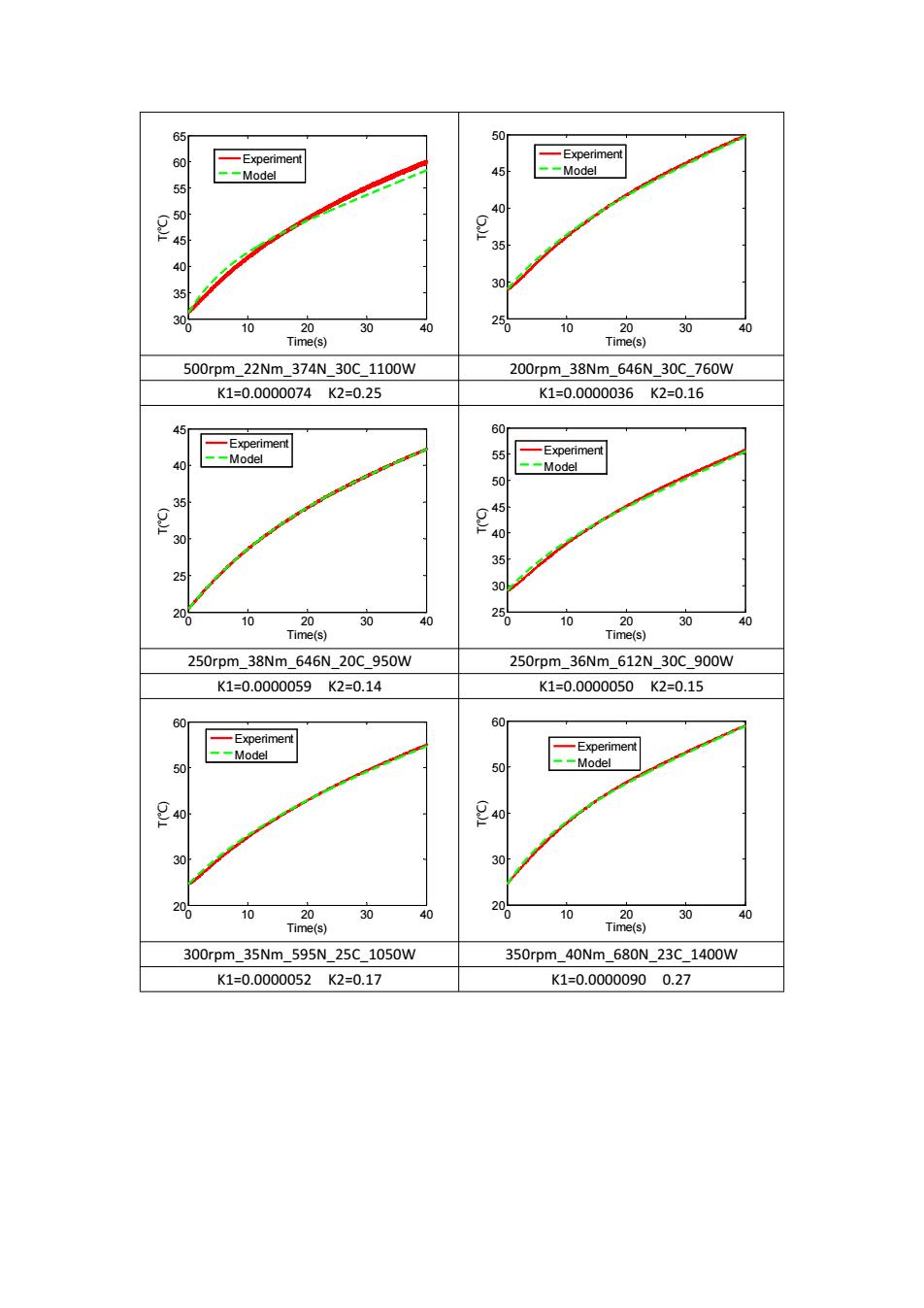
50 一Experiment -Experiment --Model AS --Model 55 50 40 45 35 30 35 10 20 30 40 % 10 20 30 40 Time(s) Time(s) 500rpm_22Nm_374N_30C_1100W 200rpm38Nm646N30C760W K1=0.0000074K2=0.25 K1=0.0000036K2=0.16 60 -Experiment 55 -Experiment 40 --Model --Model 50 45 30 35 25 30 o 10 20 30 40 10 20 30 40 Time(s) Time(s) 250rpm_38Nm_646N_20C950W 250rpm_36Nm612N_30C_900W K1=0.0000059K2=0.14 K1=0.0000050K2=0.15 60 60 -Experiment --Model -Experiment 50 -Model 30 30 200 10 20 30 40 10 20 30 40 Time(s) Time(s) 300rpm35Nm595N25C1050W 350rpm40Nm680N23C1400W K1=0.0000052K2=0.17 K1=0.00000900.27

0 10 20 30 40 30 35 40 45 50 55 60 65 Time(s) T(℃) Experiment Model 0 10 20 30 40 25 30 35 40 45 50 Time(s) T(℃) Experiment Model 500rpm_22Nm_374N_30C_1100W 200rpm_38Nm_646N_30C_760W K1=0.0000074 K2=0.25 K1=0.0000036 K2=0.16 0 10 20 30 40 20 25 30 35 40 45 Time(s) T(℃) Experiment Model 0 10 20 30 40 25 30 35 40 45 50 55 60 Time(s) T(℃) Experiment Model 250rpm_38Nm_646N_20C_950W 250rpm_36Nm_612N_30C_900W K1=0.0000059 K2=0.14 K1=0.0000050 K2=0.15 0 10 20 30 40 20 30 40 50 60 Time(s) T(℃) Experiment Model 0 10 20 30 40 20 30 40 50 60 Time(s) T(℃) Experiment Model 300rpm_35Nm_595N_25C_1050W 350rpm_40Nm_680N_23C_1400W K1=0.0000052 K2=0.17 K1=0.0000090 0.27

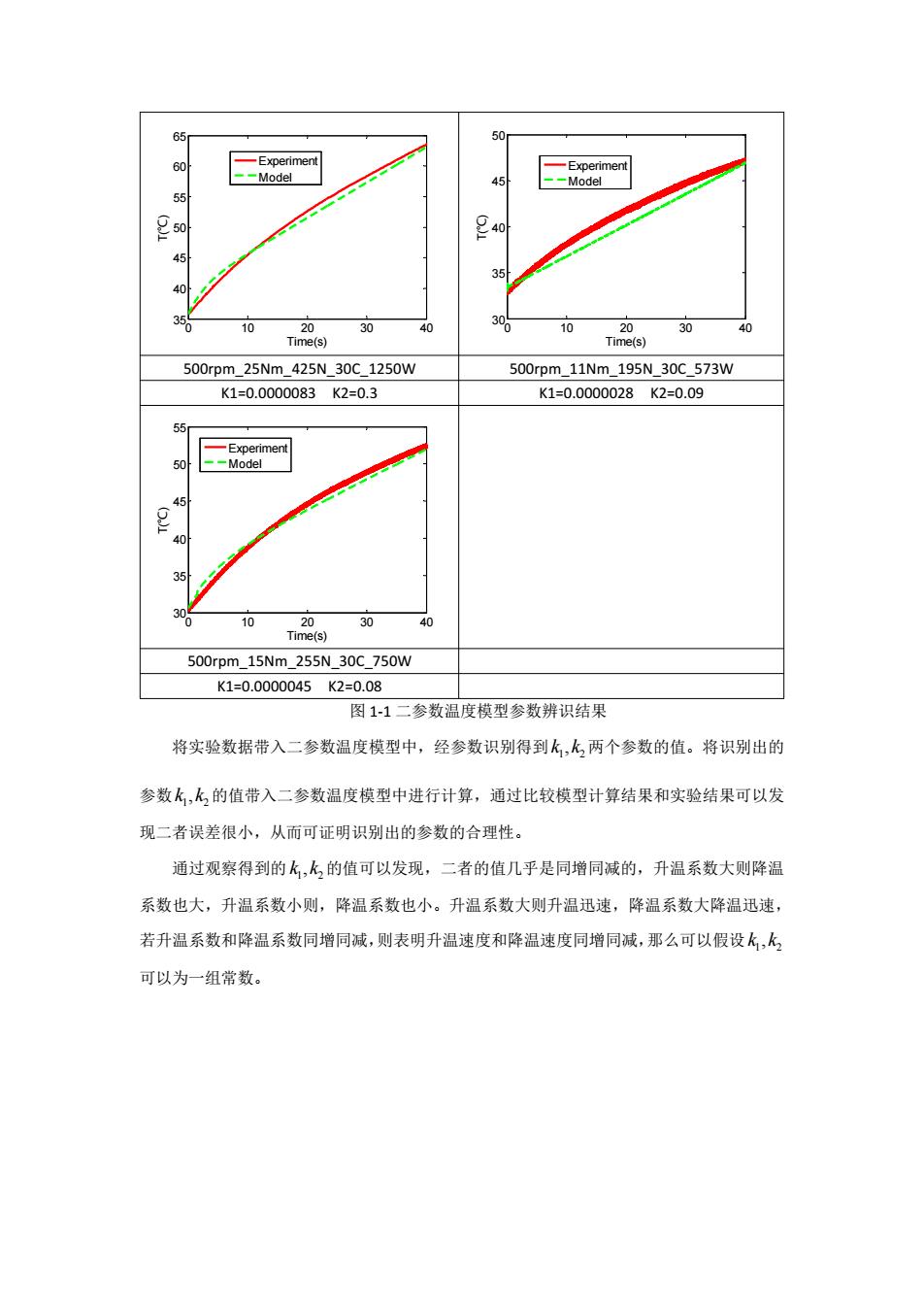
65 50 60 -Experiment -Experiment --Model 45 --Model 45 40 10 20 30 40 0 10 20 30 40 Time(s) Time(s) 500rpm_25Nm_425N_30C_1250W 500rpm11Nm195N30C573W K1=0.0000083K2=0.3 K1=0.0000028K2=0.09 55 -Experiment 50 --Model 45 90 35 30 0 10 20 30 40 Time(s) 500rpm15Nm255N_30C_750W K1=0.0000045K2=0.08 图1-1二参数温度模型参数辨识结果 将实验数据带入二参数温度模型中，经参数识别得到k,k,两个参数的值。将识别出的 参数k,k的值带入二参数温度模型中进行计算，通过比较模型计算结果和实验结果可以发 现二者误差很小，从而可证明识别出的参数的合理性。 通过观察得到的k,k的值可以发现，二者的值几乎是同增同减的，升温系数大则降温 系数也大，升温系数小则，降温系数也小。升温系数大则升温迅速，降温系数大降温迅速， 若升温系数和降温系数同增同减，则表明升温速度和降温速度同增同减，那么可以假设k,k 可以为一组常数

0 10 20 30 40 35 40 45 50 55 60 65 Time(s) T(℃) Experiment Model 0 10 20 30 40 30 35 40 45 50 Time(s) T(℃) Experiment Model 500rpm_25Nm_425N_30C_1250W 500rpm_11Nm_195N_30C_573W K1=0.0000083 K2=0.3 K1=0.0000028 K2=0.09 0 10 20 30 40 30 35 40 45 50 55 Time(s) T(℃) Experiment Model 500rpm_15Nm_255N_30C_750W K1=0.0000045 K2=0.08 图 1-1 二参数温度模型参数辨识结果 将实验数据带入二参数温度模型中，经参数识别得到 1 2 k ,k 两个参数的值。将识别出的 参数 1 2 k ,k 的值带入二参数温度模型中进行计算，通过比较模型计算结果和实验结果可以发 现二者误差很小，从而可证明识别出的参数的合理性。 通过观察得到的 1 2 k ,k 的值可以发现，二者的值几乎是同增同减的，升温系数大则降温 系数也大，升温系数小则，降温系数也小。升温系数大则升温迅速，降温系数大降温迅速， 若升温系数和降温系数同增同减，则表明升温速度和降温速度同增同减，那么可以假设 1 2 k ,k 可以为一组常数

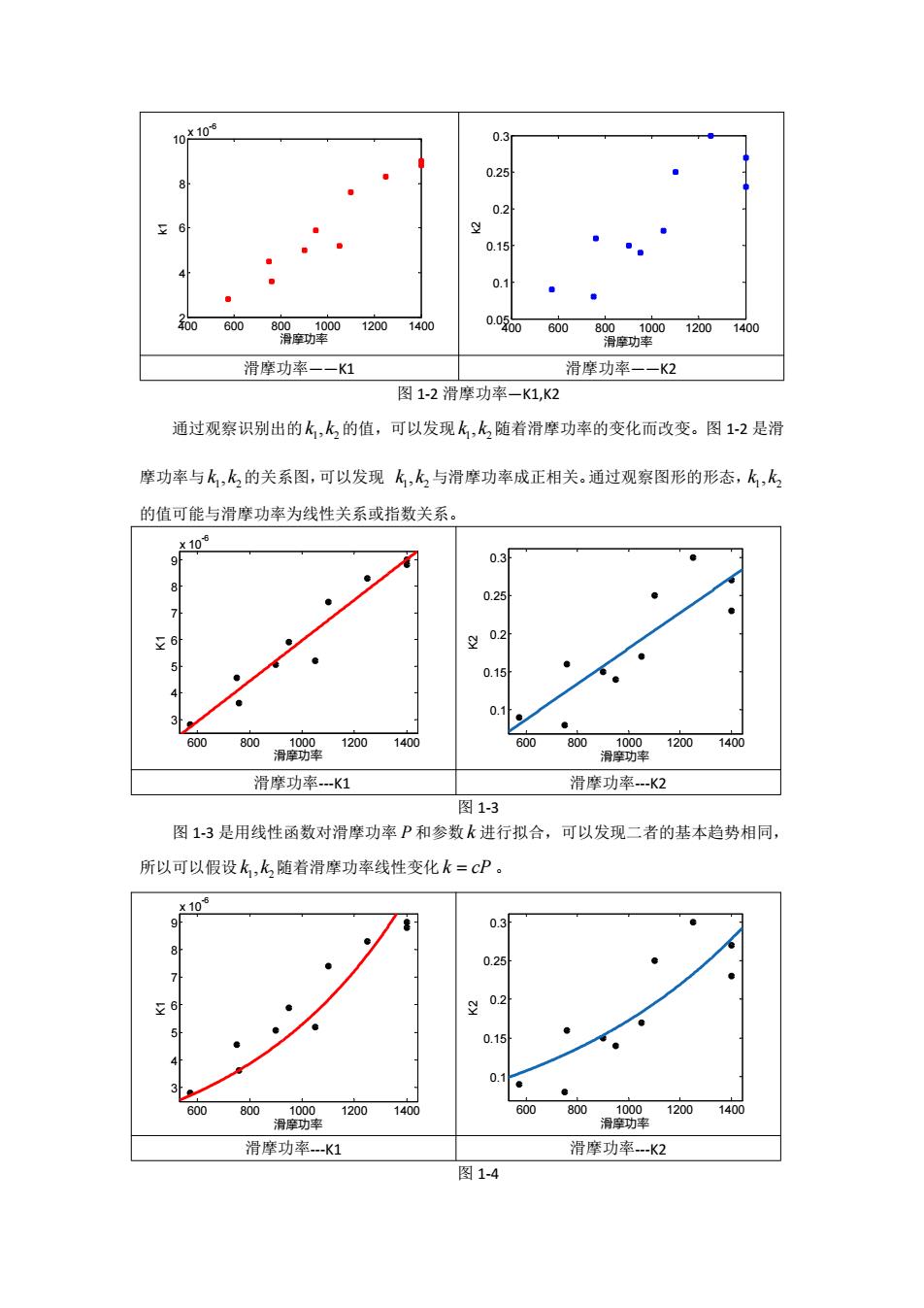
10'10s 0.25 0.2 ￥6 0.15 0.1 00 600 800 000 12001400 0.000 6008001000 12001400 滑摩功率 滑摩功率 滑摩功率一一K1 滑摩功率一一K2 图1-2滑摩功率一K1,K2 通过观察识别出的k,k的值，可以发现k,k随着滑摩功率的变化而改变。图1-2是滑 摩功率与k,的关系图，可以发现k,k与滑摩功率成正相关。通过观察图形的形态，k,k 的值可能与滑摩功率为线性关系或指数关系。 106 0.3 8 0.25 ￥6 义 0.2 0.15 0.1 ● 600 800 1000 1200 1400 600800100012001400 滑摩功率 滑摩功率 滑摩功率.-K1 滑摩功率-K2 图1-3 图13是用线性函数对滑摩功率P和参数k进行拟合，可以发现二者的基本趋势相同， 所以可以假设k,k随着滑摩功率线性变化k=cP。 106 9 0.3 0.25 6 义 0.2 0.15 0.1 600 800 1000 1200 1400 600 800 1000 12001400 滑摩功率 滑摩功率 滑摩功率.-K1 滑摩功率.-K2 图1-4

400 600 800 1000 1200 1400 2 4 6 8 10 x 10 -6 滑摩功率 k1 400 600 800 1000 1200 1400 0.05 0.1 0.15 0.2 0.25 0.3 k2 滑摩功率 滑摩功率——K1 滑摩功率——K2 图 1-2 滑摩功率—K1,K2 通过观察识别出的 1 2 k ,k 的值，可以发现 1 2 k ,k 随着滑摩功率的变化而改变。图 1-2 是滑 摩功率与 1 2 k ,k 的关系图，可以发现 1 2 k ,k 与滑摩功率成正相关。通过观察图形的形态， 1 2 k ,k 的值可能与滑摩功率为线性关系或指数关系。 600 800 1000 1200 1400 3 4 5 6 7 8 9 x 10 -6 滑摩功率 K1 600 800 1000 1200 1400 0.1 0.15 0.2 0.25 0.3 滑摩功率 K2 滑摩功率---K1 滑摩功率---K2 图 1-3 图 1-3 是用线性函数对滑摩功率 P 和参数 k 进行拟合，可以发现二者的基本趋势相同， 所以可以假设 1 2 k ,k 随着滑摩功率线性变化 k  cP 。 600 800 1000 1200 1400 3 4 5 6 7 8 9 x 10 -6 滑摩功率 K1 600 800 1000 1200 1400 0.1 0.15 0.2 0.25 0.3 滑摩功率 K2 滑摩功率---K1 滑摩功率---K2 图 1-4