
对于这两种预测方法,预测结果的得出可以通过讨论的形式直接得出,也可以使用“主观概 率法”,即先由预测专家对预测事件发生的概率作出主观的估计,然后计算它们的平均值,以此作 为对事件预测的结论 这种方法的优点是:(1)预测速度快、成本低,易于组织进行:(2)能够集思广益,相互启发 避免个人判断的局限性。其缺点是:(1)预测结果易受讨论气氛、权威人士和当时市场形势的影申: (②)对问题的分析缺乏系统的数据。 2)专家意见法 专家意见法是指专家以自己的专业知识和经验 在对过去发生的事件和历史信息资料进行综 合分析的基础上,对房地产未来可能出现的各种趋势作出判断和预测的一种方法。这里的专家包 括开发商、代理经销商、营销顾问、房地产研究工作者以及房地产协会组织。专家意见法可以分 为专家会议法和专家征询法两种形式。 (1)专家会议法 这种方法 一般由预测组织者邀请有关专 ,针对某 一开发项目或某 问题 进行开会讨论 找出问题的核心 并得出比较接近市场实际的预测结果 专家预测的具体方式有许多种 。例如 可以组织一个专家小组进行某项预测,最后可以形成一个小组估计,或者是由一位较权威的分初 家把意见汇总成个人的估计。 这种预测方法的优点是,专家集体占有的资料和考虑的问题一般要多于个人,在一起过论可 家后发,集思广益,能迅速全面地作出预测。但由于这种专家预测是以集体的形式进打 一起,容易使小组内各专家成员屈于权威或碍于情面而不愿 发表意见 受到其他因素的影响而不能畅所欲言地发表各自的意见,加上参加的人数有限,往往使代表性不 够充分。 (2)专家征询法 这种方法也叫特尔菲法。持尔菲法是羊国兰旗公司干1964年提出并首先用干技术预测领域的 预测方法。特尔菲法是专家会议法的政进和发展。由于兰德公司的专家们针对专家会议法的缺陷 提出了有效的改进措施,特尔菲法已大大提高了其适用性和预测结论的可靠性 专家们认为,特 尔菲法是一种最可靠的预测方法。 与传统的专家会议法相比,特尔菲法具备如下3大特点: ①匿名性。特尔菲法彻底改革了传统的专家会议法。不再激专家聚在一起来诵过会议的形 式研究问题。而是采用匿名函询的方式征求专家们的意见。这样,参加预测的专家互不相见,从 而消除了很多心理因素的影响,有助于专家发表较为 观的意见 ②反馈性。特尔菲法在预测过程中,一般都要进行三至五轮的征询专家意见。预测机构对每 轮专家意见均进行统计、汇总,提供给专家作下轮预测时的参考。由于多次信息交流,便于专家 比拉分析,修正意见,从而提高预测的准确程度 ③统计性。特尔菲法对每轮预测结果郑讲行定量的统计处理和评价,从而便于科学地描术议 轮预测结果中专家们意见的分布情况和分歧所在,也便于从众多的意见中归纳出基本的、 致 的、主流的意见。 特尔菲法实质上是利用专家的知识和经验对那些带有很大模糊性、较复杂的问题,通过多次 填写征询意见表的调查形式取得预测结论的预测方法。它特别适用于大规模、大范围、高难度, 复杂问题的顾测。如大多数的社会政治问题,大多数的宏观经济,地区经济、行业经济发展问题。 在房地产经营预测中 主要用于全国或地区房地产业发展趋势的预测,大规模城市改造或城市规 划方案的研究,大型项目开发方案及前景趋势预测等 2.历史引申法 这是定量预测方法的统称。在占有若干统计资料、预测对象的未来受突发性因素影响较小的 情况下,选用适当的数学模型进行定量预测,可以得到比较满意的预测效果。但是,由于所选择 16
16 对于这两种预测方法,预测结果的得出可以通过讨论的形式直接得出,也可以使用“主观概 率法”,即先由预测专家对预测事件发生的概率作出主观的估计,然后计算它们的平均值,以此作 为对事件预测的结论。 这种方法的优点是:(1)预测速度快、成本低,易于组织进行;(2)能够集思广益,相互启发, 避免个人判断的局限性。其缺点是:(1)预测结果易受讨论气氛、权威人士和当时市场形势的影响; (2)对问题的分析缺乏系统的数据。 2)专家意见法 专家意见法是指专家以自己的专业知识和经验,在对过去发生的事件和历史信息资料进行综 合分析的基础上,对房地产未来可能出现的各种趋势作出判断和预测的一种方法。这里的专家包 括开发商、代理经销商、营销顾问、房地产研究工作者以及房地产协会组织。专家意见法可以分 为专家会议法和专家征询法两种形式。 (1)专家会议法 这种方法一般由预测组织者邀请有关专家,针对某一开发项目或某一问题,进行开会讨论, 找出问题的核心,并得出比较接近市场实际的预测结果。专家预测的具体方式有许多种。例如, 可以组织一个专家小组进行某项预测,最后可以形成一个小组估计,或者是由一位较权威的分析 家把意见汇总成个人的估计。 这种预测方法的优点是,专家集体占有的资料和考虑的问题一般要多于个人,在一起讨论可 以互相启发,集思广益,能迅速全面地作出预测。但由于这种专家预测是以集体的形式进行的, 专家们面对面地坐在一起,容易使小组内各专家成员屈于权威或碍于情面而不愿发表意见,或者 受到其他因素的影响而不能畅所欲言地发表各自的意见,加上参加的人数有限,往往使代表性不 够充分。 (2)专家征询法 这种方法也叫特尔菲法。特尔菲法是美国兰德公司于 1964 年提出并首先用于技术预测领域的 预测方法。特尔菲法是专家会议法的改进和发展。由于兰德公司的专家们针对专家会议法的缺陷 提出了有效的改进措施,特尔菲法已大大提高了其适用性和预测结论的可靠性。专家们认为,特 尔菲法是一种最可靠的预测方法。 与传统的专家会议法相比,特尔菲法具备如下 3 大特点: ①匿名性。特尔菲法彻底改革了传统的专家会议法。不再邀请专家聚在一起来通过会议的形 式研究问题。而是采用匿名函询的方式征求专家们的意见。这样,参加预测的专家互不相见,从 而消除了很多心理因素的影响,有助于专家发表较为客观的意见。 ②反馈性。特尔菲法在预测过程中,一般都要进行三至五轮的征询专家意见。预测机构对每 轮专家意见均进行统计、汇总,提供给专家作下轮预测时的参考。由于多次信息交流,便于专家 比较分析,修正意见,从而提高预测的准确程度。 ③统计性。特尔菲法对每轮预测结果都进行定量的统计处理和评价,从而便于科学地描述这 一轮预测结果中专家们意见的分布情况和分歧所在,也便于从众多的意见中归纳出基本的、一致 的、主流的意见。 特尔菲法实质上是利用专家的知识和经验对那些带有很大模糊性、较复杂的问题,通过多次 填写征询意见表的调查形式取得预测结论的预测方法。它特别适用于大规模、大范围、高难度、 复杂问题的顾测。如大多数的社会政治问题,大多数的宏观经济,地区经济、行业经济发展问题。 在房地产经营预测中,主要用于全国或地区房地产业发展趋势的预测,大规模城市改造或城市规 划方案的研究,大型项目开发方案及前景趋势预测等。 2.历史引申法 这是定量预测方法的统称。在占有若干统计资料、预测对象的未来受突发性因素影响较小的 情况下,选用适当的数学模型进行定量预测,可以得到比较满意的预测效果。但是,由于所选择

和建立的数学模型不可能把所有因素都考虑进去,因此定量预测的结果出现误差也在所难免。此 种方法包括简单平均数法、移动平均数法、加权移动平均数法、趋势预测法、指数平滑法和季节 指数法等 1)简单平均数法 简单平均数法是用算术平均值作为新一期的预测值的方法。即在时间序列的几个实际值x, ,X,x中,求出它们的算术平均值作为新一期的预测值。 其计算公式如下: 隆=-多达 n 式中:x一代表平均数,即用算术平均法进行预测时的预测值:一代表资料数:X。一代表第 期的实际销售数1=1,2,3. 某房地产公司1 -6月的实际销售量见表2-1。试预测该公司7月份销售量。 表2一 某房地产公司1一6月销售量 月份 1 2 3 4 5 6 实际销售量4400 5000 4500 6000 5500 7000 解:按简单平均数公式(2.),预测7月份销售量为: 6=7=400+5000+4500+600+50+700=5400(平方米) 6 从这个例子可以看出,用简单平均法来预测7月份的销售量,其预测值为540平方米。但此 飘测方法能销告量比较平商的情况下无用。如果销售量波动情况较大时。采用此方法进行形 其误差就比较大。 2)移动平均法 移动平均法是在简单平均法的基础上发展起来的,短期预测中应用较多。其做法是把被平均 的项逐渐向后移动加以平均,每项平均的总项数不变。这个平均数就直接作为下期的预测值。平 均时,可以用简单的算术平均数,也可以用加权平均数(此种方法对近期的最新实际销售量较为重 所以 数也最大 至于以前各期 的实际销售量, 则愈早 者所加 权数也愈小。 它可以在销 波动较大的情况下预测下期销售量。越近期的数字,用的权数越大。此时移动平均法变成了加权 移动平均法)。后一种方法的准确性较高,其优点在于不断吸收最新观察值、不断舍弃远期观察值, 这对提高预测的精度是有利的。 简单移动平均法的计算公式为: x=k,+x+.+x-) (2.2) 加权移动平均法的计算公式为: m,+(0n-l0x+.+X-a-l (2.3) n+(n-1)+.+2+1 由公式可见,不论简单式还是加权式,只能预测下一期数值 例2-2某房地产公司1999一2002年的商品房实际销售量见表2-2,试用移动平均法预测 2003年以后的销售量。 表2一一2 1999-2002年的销售量单位:平方米 年份 1999 2000 2001 2002 17
17 和建立的数学模型不可能把所有因素都考虑进去,因此定量预测的结果出现误差也在所难免。此 种方法包括简单平均数法、移动平均数法、加权移动平均数法、趋势预测法、指数平滑法和季节 指数法等。 1)简单平均数法 简单平均数法是用算术平均值作为新一期的预测值的方法。即在时间序列的几个实际值 x1, x2,x3,.xn 中,求出它们的算术平均值作为新一期的预测值。 其计算公式如下: 预测值= x = n x x x x 1 + 2 + 3 ++ n = n x n i i =1 式中: x —代表平均数,即用算术平均法进行预测时的预测值;n—代表资料数;xn—代表第 j 期的实际销售数(i=1,2,3,.n)。 例2-1 某房地产公司 1-6 月的实际销售量见表 2-1。试预测该公司 7 月份销售量。 表 2-1 某房地产公司 1-6 月销售量 月份 1 2 3 4 5 6 实际销售量 4400 5000 4500 6000 5500 7000 解:按简单平均数公式(2.1),预测 7 月份销售量为: x7= x = 6 4400 + 5000 + 4500 + 6000 + 5500 + 7000 =5400(平方米) 从这个例子可以看出,用简单平均法来预测 7 月份的销售量,其预测值为 5400 平方米。但此 预测方法只能在销售量比较平衡的情况下采用,如果销售量波动情况较大时,采用此方法进行预 测,其误差就比较大。 2)移动平均法 移动平均法是在简单平均法的基础上发展起来的,短期预测中应用较多。其做法是把被平均 的项逐渐向后移动加以平均,每项平均的总项数不变。这个平均数就直接作为下期的预测值。平 均时,可以用简单的算术平均数,也可以用加权平均数(此种方法对近期的最新实际销售量较为重 视,所以权数也最大。至于以前各期的实际销售量,则愈早者所加权数也愈小。它可以在销售量 波动较大的情况下预测下期销售量。越近期的数字,用的权数越大。此时移动平均法变成了加权 移动平均法)。后一种方法的准确性较高,其优点在于不断吸收最新观察值、不断舍弃远期观察值, 这对提高预测的精度是有利的。 简单移动平均法的计算公式为: t+1 x = ( ) 1 ( 1) 1 t + t− + + t− n− x x x n (2.2) 加权移动平均法的计算公式为: t+1 x = ( 1) 2 1 ( 1) 1 ( 1) + − + + + + − − + + − − n n nx n x x t t t n (2.3) 由公式可见,不论简单式还是加权式,只能预测下一期数值。 例 2-2 某房地产公司 1999-2002 年的商品房实际销售量见表 2-2,试用移动平均法预测 2003 年以后的销售量。 表 2--2 1999-2002 年的销售量 单位:平方米 年份 1999 2000 2001 2002

实际销售量6700 5500 6900 7600 解:在预测2003年商品房销售量时: 如用简单移动平均数,计算结果为: 2003年预测值= 6700+5500+6900+7600 =6675(平方米) A 如用加权移动平均数,计算结果为 203年预测值=6700x1+50x2+6900x3+7600×4-680(年方米 4+3+2+1 在预测2004年商品房销售量时: 如用简单移动平均数,计算结果为: 204年预测值=500+6900+7600+675=668.75方米 如用加权移动平均数,计算结果为: 2034年预测值=500×1+6900x2+7600×3+6880×4=6272(年方米 4+3+2+1 由干这种方法主要是不断引讲新的数据来修正平均值,以消除销售量变动的不稳定因素,而 且还可以看出其发展趋势,所以在投资分析中, 一般应结合趋势预测法使用。 3)趋势预测法 这是历史引申法中最适合于中长期预测的方法。其基本原理是:根据过去各期的实际数据, 分析其发展趋势,并假定今后按该趋势继续发展,从而测定今后各期的数据。如果过去各期数据 大体呈现等差级数,则其变化趋势可用直线方程来表示:如果过去各期数据大体呈现等比级数, 则可用曲线方程来表示 在这里,我们只介绍直线趋势方程。 求趋势直线的方程式是:y=a十bx 式中:y一预测值:X一代表的年份:a,b一待定系数。 运用最小二乘法求得如下方程组: a=∑-b∑x b=ny-∑∑y n∑x2-∑x,P 令∑x,=0,则上式可简化为 ∑xy 式中:y:一各年的实际销售量:x:一各年的代号:n一己掌握数据的年数。 例2-3某城市住宅物业1997一2002年间各年的价格变化情况的统计数据见表2-3,要求 预测2004年该类物业的市场单价。 18
18 实际销售量 6700 5500 6900 7600 解:在预测 2003 年商品房销售量时: 如用简单移动平均数,计算结果为: 2003 年预测值= 4 6700 + 5500 + 6900 + 7600 =6675(平方米) 如用加权移动平均数,计算结果为: 2003 年预测值= 4 3 2 1 6700 1 5500 2 6900 3 7600 4 + + + + + + =6880(平方米) 在预测 2004 年商品房销售量时: 如用简单移动平均数,计算结果为: 2004 年预测值= 4 5500 + 6900 + 7600 + 6675 =6668.75(平方米) 如用加权移动平均数,计算结果为: 2034 年预测值= 4 3 2 1 5500 1 6900 2 7600 3 6880 4 + + + + + + =6272(平方米) 由于这种方法主要是不断引进新的数据来修正平均值,以消除销售量变动的不稳定因素,而 且还可以看出其发展趋势,所以在投资分析中,一般应结合趋势预测法使用。 3)趋势预测法 这是历史引申法中最适合于中长期预测的方法。其基本原理是:根据过去各期的实际数据, 分析其发展趋势,并假定今后按该趋势继续发展,从而测定今后各期的数据。如果过去各期数据 大体呈现等差级数,则其变化趋势可用直线方程来表示;如果过去各期数据大体呈现等比级数, 则可用曲线方程来表示。 在这里,我们只介绍直线趋势方程。 求趋势直线的方程式是:y=a+bx 式中:y—预测值;x—代表的年份;a,b—待定系数。 运用最小二乘法求得如下方程组: a= n y b x i − i b= ( ) − − 2 2 i i i i i i n x x n x y x y 令 xi = 0 ,则上式可简化为: a= n y i b= 2 i i i x x y 式中:yi—各年的实际销售量;xi—各年的代号;n—已掌握数据的年数。 例 2-3 某城市住宅物业 1997-2002 年间各年的价格变化情况的统计数据见表 2-3,要求 预测 2004 年该类物业的市场单价
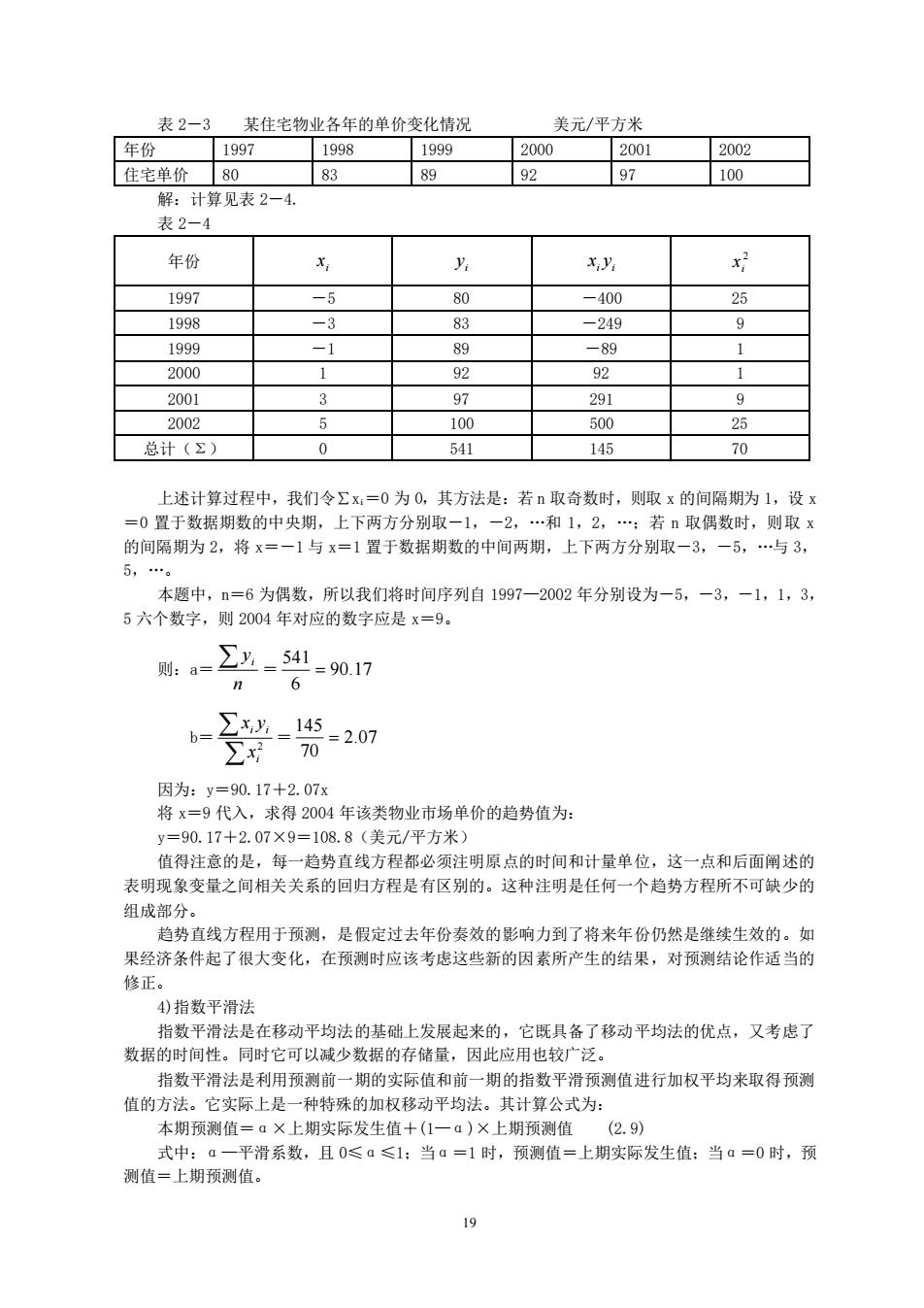
表2一3 其住字物业冬年的单价变化桔况 美元/平方米 年份 1997 1998 1999 2000 2001 2002 住宅单价 80 83 89 97 100 解:计算见表2-4 表2-4 年份 y 1997 -5 80 -400 25 1998 -3 83 -249 1999 1 89 -89 2000 92 2001 97 291 2002 100 500 25 总计(Σ) 541 145 70 上述计算过程中,我们令Σx=0为0,其方法是:若取奇数时,则取x的间隔期为1,设x =0置于数据期数的中央期,上下两方分别取一1,一2,.和1,2,:若n取偶数时,则取x 的间隔期为2,将x=一1与x=1置于数据期数的中间两期,上下两方分别取一3,-5,与3, 本题中,n=6为偶数,所以我们将时间序列自1997 -2002年分别设为-5,-3,-1,1,3, 5六个数字,则2004年对应的数字应是x=9。 则:a=∑上-541 90.17 n 6 ∑xy_145 -2.07 ∑x 70 因为:y=90.17+2.07x 将x=9代入,求得2004年该类物业市场单价的趋势值为: =90.17+2.07×9=108.8(美元/平方米) 值得注意的是,每一趋势直线方程都必须注明原点的时间和计量单位,这一点和后面阐述的 表明现象变量之间相关关系的回归方程是有区别的。这种注明是任何一个趋势方程所不可缺少的 组成部分。 趋势直线方程用于预测,是假定过去年份奏效的影响力到了将来年份仍然是继续生效的。如 果经济条件起了很大变化,在预测时应该考虑这些新的因素所产生的结果,对预测结论作适当的 修正 4)指数平滑法 指数平滑法是在移动平均法的基础上发展起来的,它既具各了移动平均法的优点,又考虑了 数据的时间性。同时它可以减少数据的存储量,因此应用也较广泛。 指数平滑法是利用预测前一期的实际值和前一期的指数平滑预测值进行加权平均来取得预测 值的方法。它实际上是一种特殊的加权移动平均法。其计算公式为 本期预测值=α×上期实际发生值十( -a)X上 期预测信 (2.9 式中:a一平滑系数,且0≤ā≤1:当a=1时,预测值=上期实际发生值:当a=0时,预 测值=上期预测值。 19
19 表 2-3 某住宅物业各年的单价变化情况 美元/平方米 年份 1997 1998 1999 2000 2001 2002 住宅单价 80 83 89 92 97 100 解:计算见表 2-4. 表 2-4 年份 i x i y i i x y 2 i x 1997 -5 80 -400 25 1998 -3 83 -249 9 1999 -1 89 -89 1 2000 1 92 92 1 2001 3 97 291 9 2002 5 100 500 25 总计(Σ) 0 541 145 70 上述计算过程中,我们令∑xi=0 为 0,其方法是:若 n 取奇数时,则取 x 的间隔期为 1,设 x =0 置于数据期数的中央期,上下两方分别取-1,-2,.和 1,2,.;若 n 取偶数时,则取 x 的间隔期为 2,将 x=-1 与 x=1 置于数据期数的中间两期,上下两方分别取-3,-5,.与 3, 5,.。 本题中,n=6 为偶数,所以我们将时间序列自 1997—2002 年分别设为-5,-3,-1,1,3, 5 六个数字,则 2004 年对应的数字应是 x=9。 则:a= n y i = 90.17 6 541 = b= 2 i i i x x y = 2.07 70 145 = 因为:y=90.17+2.07x 将 x=9 代入,求得 2004 年该类物业市场单价的趋势值为: y=90.17+2.07×9=108.8(美元/平方米) 值得注意的是,每一趋势直线方程都必须注明原点的时间和计量单位,这一点和后面阐述的 表明现象变量之间相关关系的回归方程是有区别的。这种注明是任何一个趋势方程所不可缺少的 组成部分。 趋势直线方程用于预测,是假定过去年份奏效的影响力到了将来年份仍然是继续生效的。如 果经济条件起了很大变化,在预测时应该考虑这些新的因素所产生的结果,对预测结论作适当的 修正。 4)指数平滑法 指数平滑法是在移动平均法的基础上发展起来的,它既具备了移动平均法的优点,又考虑了 数据的时间性。同时它可以减少数据的存储量,因此应用也较广泛。 指数平滑法是利用预测前一期的实际值和前一期的指数平滑预测值进行加权平均来取得预测 值的方法。它实际上是一种特殊的加权移动平均法。其计算公式为: 本期预测值=α×上期实际发生值+(1—α)×上期预测值 (2.9) 式中:α—平滑系数,且 0≤α≤1;当α=1 时,预测值=上期实际发生值;当α=0 时,预 测值=上期预测值

在实际工作中,平滑系数一般是根据原预测数与实际数的差异大小来确定。如果差异较大时, a应适当取较大值:如果差异较小时, 应适当取较小值。为了计算方便 般根据经验估计 当差异较大时,a取0.7-0.8为宜:当差异较小时,▣取0.2-0.3为宜 运用指数平滑法,需要估计初始值,即最早预测值。它不能从基本公式中获得,只能加以估 计。比较简单的办法就是选取前若干个观察值求出平均值作为初始值,或用最早的实际值直接代 替预测值。下例中,2002年7月份的预测值就是通过此前若干个月的观察值求出的平均值。 例2-4某房地产公司2002年7一12月份实际销售额及预测值见表2-5。如果设=0.3, 求2003年1月份销售量的预测值 表2-5 2002 2月份实际销售预测值 单位: 平方米 月份 实际销售量 预测值 5000 5200 4800 5000 5200 5300 10 4900 5000 11 5500 5200 12 6000 5800 1月份预测值=ā×上期实际销售量+(1一ā)×上期预测值 =0.3×6000+(1-0.3)×5800 =1800+4060=5860(平方米) 即2003年1月份的销售预测值为5860平方米 5)季节指数法 某些产品的销售量,受季节变化的影响很明显。在每一年里,随月份、季节的不同,有不同 的变动趋势。比如电风扇、电褥子的需求量每年都有变动,但电风扇的需求量明显夏季高于冬季, 而申褥子的需求量冬季明显高于夏委。房地产需求量随季节不同也有一定的变化规使,只不过其 规律更复杂,影响其变化规律的因素更多些而己。 作为 一个经营管理人员,要留意掌握各种商品 的季节特性, 采取相应措施 才能适时地准备好供应。为此需要对 一些特定商品进行季节性预测 季节性预测比较简单的方法是计算各个季度的不同销售指数。季节销售指数可利用简单平均 法算出。它是根据历史资料求出每季度平均数占全期总平均数的比例,以表明各季销售水平比全 期总销售水平高低的程度。其预测步骤为 第1北:求出历年各委的平均销售量 第2步 求出各季的季节指数 即 季的平均数占全年平均数总和的百分比 第3步:根据季节指数和已知某年某季的实际数预测该年其他各个季的数据。 例2一5某房地产公司1998年第1季度到2002年第4季度实际销售量见表2一6,如果预测 2003年销售量为89200平方米,要求预测第3、4季度的销售量。 1998一2002年各季度的销售量单位:平方米 、季度 2 4 合计 年份 1998 13800 18700 27500 17500 77500 1000 1A200 10800 96500 18400 79000 2000 13100 19400 24500 17000 74000 2001 1570% 20000 28300 1940 83400 2002 15000 21400 27000 18500 82500 △+ 71900 99300 134400 90800 396400 20
20 在实际工作中,平滑系数一般是根据原预测数与实际数的差异大小来确定。如果差异较大时, α应适当取较大值;如果差异较小时,α应适当取较小值。为了计算方便,一般根据经验估计, 当差异较大时,α取 0.7—0.8 为宜;当差异较小时,α取 0.2-0.3 为宜。 运用指数平滑法,需要估计初始值,即最早预测值。它不能从基本公式中获得,只能加以估 计。比较简单的办法就是选取前若干个观察值求出平均值作为初始值,或用最早的实际值直接代 替预测值。下例中,2002 年 7 月份的预测值就是通过此前若干个月的观察值求出的平均值。 例 2-4 某房地产公司 2002 年 7—12 月份实际销售额及预测值见表 2—5。如果设α=0.3, 求 2003 年 1 月份销售量的预测值。 表 2-5 2002 年 7-12 月份实际销售预测值 单位:平方米 月份 实际销售量 预测值 7 5000 5200 8 4800 5000 9 5200 5300 10 4900 5000 11 5500 5300 12 6000 5800 解: 1 月份预测值=α×上期实际销售量+(1-α)×上期预测值 =0.3×6000+(1-0.3)×5800 =1800+4060=5860(平方米) 即 2003 年 1 月份的销售预测值为 5860 平方米。 5)季节指数法 某些产品的销售量,受季节变化的影响很明显。在每一年里,随月份、季节的不同,有不同 的变动趋势。比如电风扇、电褥子的需求量每年都有变动,但电风扇的需求量明显夏季高于冬季, 而电褥子的需求量冬季明显高于夏季。房地产需求量随季节不同也有一定的变化规律,只不过其 规律更复杂,影响其变化规律的因素更多些而已。作为一个经营管理人员,要留意掌握各种商品 的季节特性,采取相应措施,才能适时地准备好供应。为此需要对一些特定商品进行季节性预测。 季节性预测比较简单的方法是计算各个季度的不同销售指数。季节销售指数可利用简单平均 法算出。它是根据历史资料求出每季度平均数占全期总平均数的比例,以表明各季销售水平比全 期总销售水平高低的程度。其预测步骤为: 第 1 步:求出历年各季的平均销售量。 第 2 步:求出各季的季节指数,即当季的平均数占全年平均数总和的百分比。 第 3 步:根据季节指数和已知某年某季的实际数预测该年其他各个季的数据。 例 2-5 某房地产公司 1998 年第 l 季度到 2002 年第 4 季度实际销售量见表 2-6,如果预测 2003 年销售量为 89200 平方米,要求预测第 3、4 季度的销售量。 表 2-6 1998—2002 年各季度的销售量 单位:平方米 季度 年份 1 2 3 4 合计 1998 13800 18700 27500 17500 77500 1999 14300 19800 26500 18400 79000 2000 13100 19400 24500 17000 74000 2001 15700 20000 28300 19400 83400 2002 15000 21400 27000 18500 82500 合计 71900 99300 134400 90800 396400