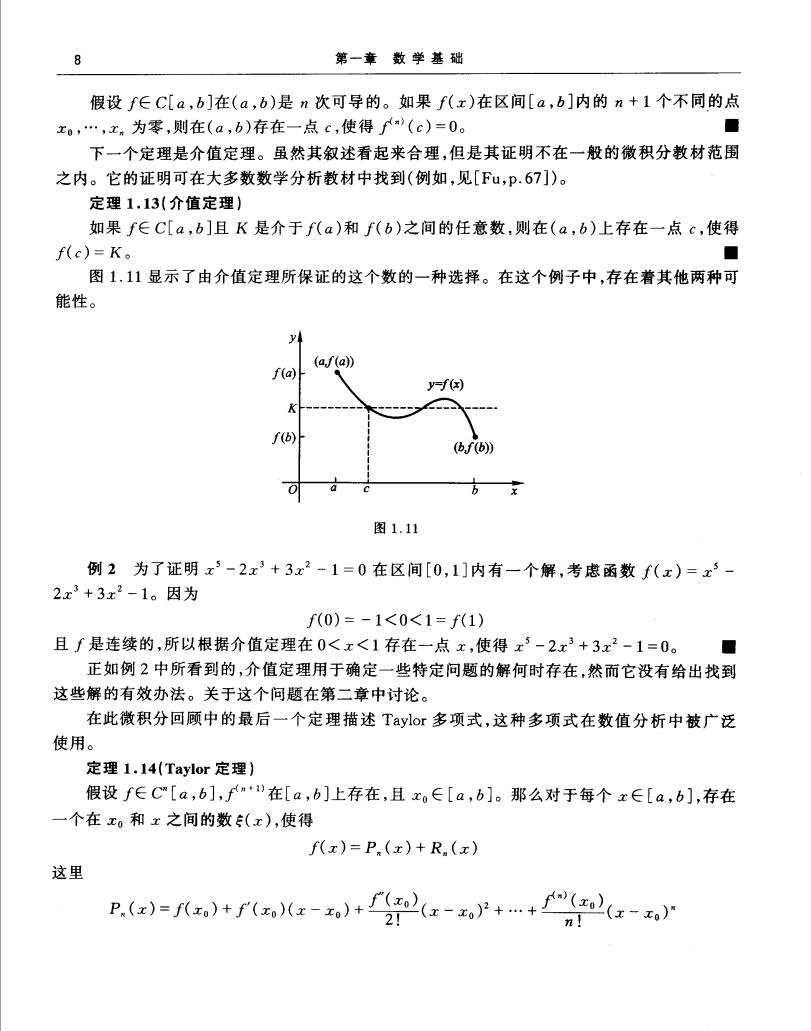
8 第一章数学基础 假设f∈C[a,b]在(a,b)是n次可导的。如果f(x)在区间[a,b]内的n+1个不同的点 xo,.,x.为零,则在(a,b)存在一点c,使得(c)=0。 ■ 下一个定理是介值定理。虽然其叙述看起来合理,但是其证明不在一般的微积分教材范围 之内。它的证明可在大多数数学分析教材中找到(例如,见[Fu,P.67])。 定理1.13(介值定理) 如果f∈C[a,b]且K是介于f(a)和f(b)之间的任意数,则在(a,b)上存在一点c,使得 f(c)=K。 图1.11显示了由介值定理所保证的这个数的一种选择。在这个例子中,存在着其他两种可 能性。 (af(a)) f(a) f(y 6 图1.11 例2为了证明x3-2x3+3x2-1=0在区间[0,1]内有一个解,考虑函数f(x)=x5 2x3+3x2-1。因为 f(0)=-1<0<1=f(1) 且∫是连续的,所以根据介值定理在0<x<1存在一点x,使得x3-2x3+3x2-1=0。■ 正如例2中所看到的,介值定理用于确定一些特定问题的解何时存在,然而它没有给出找到 这些解的有效办法。关于这个问题在第二章中讨论。 在此微积分回顾中的最后一个定理描述Taylor多项式,这种多项式在数值分析中被广泛 使用。 定理1.14(Taylor定理) 假设fC[a,b],"在[a,b]上存在,且∈[a,b]。那么对于每个x∈[a,b],存在 一个在xo和x之间的数(x),使得 f(x)=P.(x)+R.(x) 这里 P.()=x)+f✉-+fz-++fz- n!
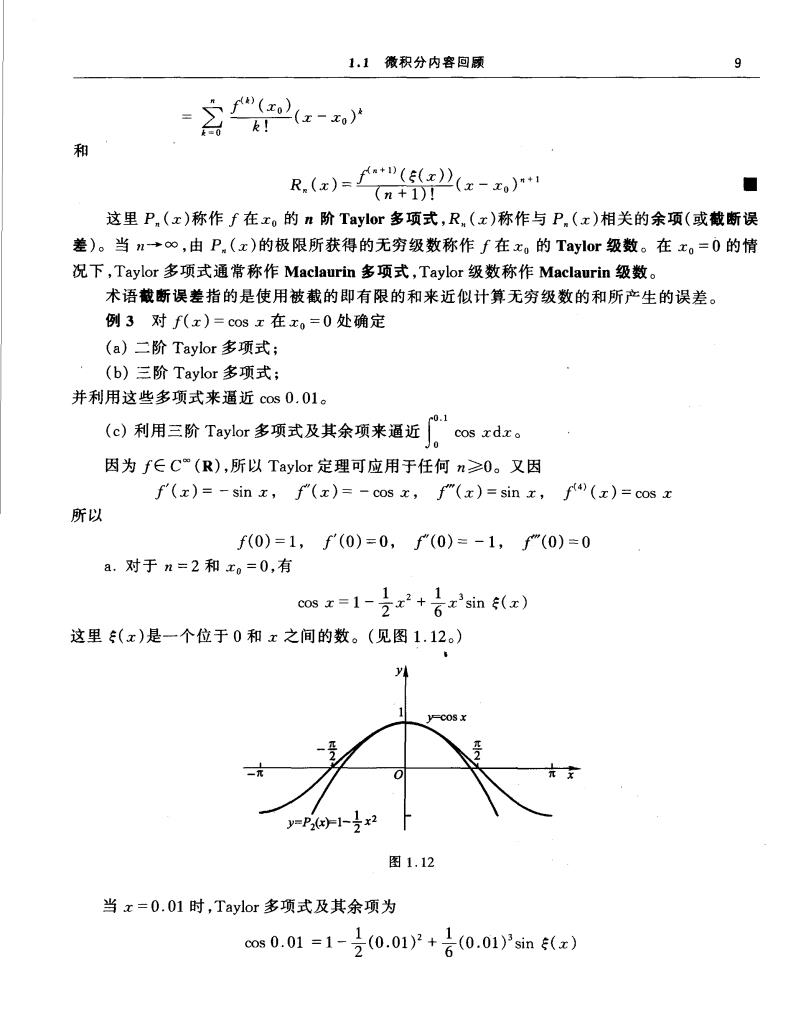
1.1微积分内容回顾 9 =2f"z- =0 k! 和 R.(e)=f02(z-. (n+1)! 这里P.(x)称作f在xo的n阶Taylor多项式,R(x)称作与P.(x)相关的余项(或截断误 差)。当n→o∞,由P.(x)的极限所获得的无穷级数称作f在x。的Taylor级数。在x。=0的情 况下,Taylor多项式通常称作Maclaurin多项式,Taylor级数称作Maclaurin级数。 术语截断误差指的是使用被截的即有限的和来近似计算无穷级数的和所产生的误差。 例3对f(x)=cosx在x,=0处确定 (a)二阶Taylor多项式; (b)三阶Taylor多项式: 并利用这些多项式来通近cos0.01。 (d)利用三阶Taylor多项式及其余项来道近。”co。 因为f∈C"(R),所以Taylor定理可应用于任何n≥0。又因 f(x)=-sinx,f(x)=-cosx,f"(x)=sinx,f(x)=cosx 所以 f0)=1,f(0)=0,f(0)=-1,"(0)=0 a.对于n=2和xo=0,有 c0=1'sin ( 这里(x)是一个位于0和x之间的数。(见图1.12) 1-x 图1.12 当x=0.01时,Taylor多项式及其余项为 os0.01=1-2(0.01)2+6(0.01)Psin(x)

10 第一章数学基础 =0.99995+0.16×10-6sin(x) 这里0<(x)<0.01。(0.16中6上面的一圆点用来指6这个数字无限地重复下去)因为 |sin(x)|<1对所有x成立,所以有 1cos0.01-0.99995|≤0.16×106 所以近似值0.99995至少精确到cos0.01的前5位数字,且 0.9999483<0.99995-1.6×106≤cos0.01 ≤0.99995+1.6×106<0.9999517 误差界比实际误差大许多,部分原因是由于我们对|si(x)川所使用的上界不好。可以证 明对所有x值,有sinx≤|x。因为0≤<0.01,所以在误差公式中,如果利用 1sin(x)≤0.01这个事实,就可得到误差界0.16×108。 b,因为"(O)=0,所以在xo=0具有余项的三阶Taylor多项式是 sx=1-是r2+co(x) 这里0<E(x)<0.01。通近多项式依然是相同的,近似值仍是0.99995,但是现在有更好的精 度保证。因为|cosE(x)川≤1对于所有x成立,所以有 1 2 cos(x)≤2a(0.01)r(1)≈4.2×100 因而 c0s0.01-0.999951≤4.2×10-0 令 0.99994999958=0.99995-4.2×1010 ≤cos0.01≤0.99995+4.2×10-0 =0.99995000042 这个例子的前两部分说明了数值分析的两个目标。第一个目标是找到近似值,正如这两部 分中Taylor多项式所提供的。第二个目标是确定通近的精度。本例中,虽然两个多项式给出相 同的近似值,但是三阶Taylor多项式比二阶Taylor多项式的结果更进一步。 c.利用三阶Taylor多项式,有 crd)dz o()ds

1.1微积分内容回顾 11 0.cn FC)dr 所以,得 wd0.(0.0.0 根据Taylor余项的积分和|cos(x)川≤1对所有x成立的事实,此通近的误差界可以确定为 。ma✉5a1m1a ≤ara=8x0 因为这个积分的值是 co rdir sin =sin 0.1 ≈0.099833417 所以上面近似值的实际误差是8.332×10·。这个误差在误差界范围之内。 ■ 在例3中还可使用CAS。我们使用Maple定义f >f:=cos(x); Maple允许在一行放置多个语句,并用冒号来阻止Maple对语句执行的回应。例如,用下面 的命令得到三阶Taylor多项式 >s3:=taylor(f,x=0,4):p3:convert(s3,polynom); 第一部分计算出了在x。=0展开具有4项(阶为3)和展开余项的Taylor级数。第二部分通过忽 略余项将级数s3转化为多项式p3。为了得到11位十进制数字的显示,键入 >Digits:=11; 键入下面的命令来计算f(0.01),P,(0.01)和f(0.01)-P,(0.01)川的值 >y1:evalf(subs(x=0.01,f)); >y2:evalf(subs(x=0.01,p3)); >err:=abs(yl-y2); 从而得到y1=f(0.01)=0.99995000042,y2=P,(0.01)=0.99995000000,和 1f(0.01)-P3(0.01)=0.42×109。 为了得到类似于图1.12的图形,键人 >plot(If,p31,x=-Pi.Pi); 计算积分的命令是 >g1:=int(f,x=0.0.1): >g2:=int(p3,x=0.0.1):

第一章数学基础 >err:=abs(ql-q2); 从而得到 gi-)d=0.098341647和q-P,(zdz=0.0983333 误差为0.83314×10-7。 这个例子的(a)和(b)两部分说明了两种方法如何可以产生相同的近似值,但具有不同的精 度估计。注意确定近似值只是我们的部分目标,另一个同样重要的目标是至少确定近似值精度 的界值。 习题1.1 1.证明下面的方程在给定的区间内至少有一个解。 a.xc0sx-2x2+3x-1=0,[0.2,0.3]和[1.2,1.3] b.(x-2)2-lmx=0,[1,2]和[e,4] c,2xcs(2x)-(x-2)2=0,[2,3]和[3,4] d.x-(lnx)=0,[4,5] 2.找出包含下列方程之解的区间。 a.x-3=0 b.4x2-e'=0 c.x3-2x2-4x+3=0 d.x3+4.001x2+4.002x+1.101=0 3.证明∫(x)在给定的区间至少有一次值为0。 a.f(x)=1-e+(e-1)sin(x/2)x),[0,1] b.f八x)=(x-1)anx+xsin nx,[0,1] c.f(x)=xsin xr -(r-2)In ,[1,2] d.fx)=(x-2)sin xln(x+2),[-1,3] 4.对于下列的函数和区间求出警八x)引。 a.f(x)=(2-e'+2x)/3,[0,1] b.f(x)=(4x-3)八x2-2x),[0.5,1] c.f(x)=2xcos(2x)-(x-2)2,[2,4] d.fx)=1+e-n,[1,2] 5.利用介值定理和Roe定理证明不论常数k取何值,f(x)=x3+2x+k的图像恰好经过x轴一次。 6.假设f∈C[a,b]且f(x)在(a,b)上存在。证明如果f(x)≠0对一切(a,b)内的x成立,那么在 [a,b]内至多存在一点p使得f八p)=0。 7.设fx)=x3。 a.找出在xo=0的二阶Taylor多项式Pz(x)。 b.找出用P2(0.5)来通近f(0.5)的R(0.5)和实际误差