
1.1微积分内容回顾 3 下面的定理说明了收敛和连续性概念之间的关系。 定理1.4如果f是定义在实数集X上的函数且x,∈X,则下列叙述等价 a.f在xo是连续的; b.如果{工,:,是X上收敛于xn的任意数列,则1imf(x)=f(x,)。 ◆ 在讨论数值方法时假设所考虑的函数是连续的,这是因为连续性条件是对可预知行为的最 小要求。因为不连续函数可能会跳过某些我们所关注的点,这在求问题的近似解时可能造成困 难。对于函数的更严格的假设通常导致更好的逼近结果。例如,具有光滑图形的函数往往比具 有许多尖点特征的函数表现得更加可以预测。光滑性条件与导数的概念有关。 定义1.5设f是定义在含有x。的开区间上的一个函数。函数∫在xo是可微的,如果 f(z)=mfx)-f) x-xo 存在。值∫(x。)称为∫在x。的导数。在集合X上每一点都有导数的函数称为在集合X上是 可微的。 f在x。的导数是f的图形在(xo,f(xo)切线的斜率,如图1.2所示。 切线斜率为∫'(o) f(xo) (,f() y=f树 图1.2 定理1.6如果函数f在x0是可微的,则∫在x。是连续的。 ◆ 在集合X上具有n阶连续导数的所有函数的集合记为C"(X)。在集合X上具有任意阶 数的所有函数的集合记为C“(X)。多项式函数、有理函数、三角函数、指数函数和对数函数都在 C“(X)中,这里X是由函数在其上有定义的所有数值组成的。当X是实数轴上的一个区间时, 同样省略记号中的括号。 下面的一些定理在推导误差估计的方法时是十分重要的。这些定理的证明和本节中没有指 出资料来源的结果都可在一般的微积分教材中找到。 定理1.7(Rolle定理) 假设f∈C[a,b]且f在(a,b)上是可微的,若f(a)=f(b),则在(a,b)内存在一点c使得 f(c)=0。(见图1.3。) ◆
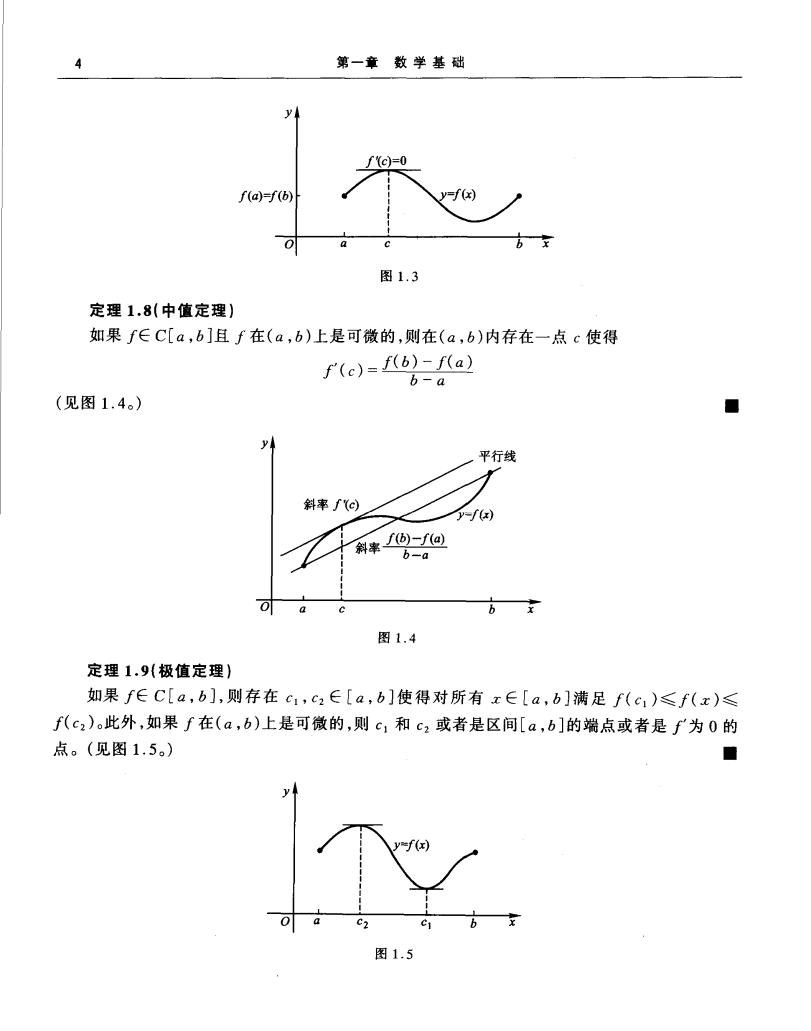
4 第一章数学基础 (a)f(b) 图1.3 定理1.8(中值定理) 如果f∈C[a,b]且f在(a,b)上是可微的,则在(a,b)内存在一点c使得 f(c)=E(b)-f(a) b-a (见图1.4。) 平行线 斜率∫e f 斜率®-@ b-a 0 图1.4 定理1.9(极值定理) 如果f∈C[a,b],则存在c1,c2∈[a,b]使得对所有x∈[a,b]满足f(c1)≤f(x)≤ f(c2)。此外,如果f在(a,b)上是可微的,则c1和c2或者是区间[a,b]的端点或者是f为0的 点。(见图1.5) ■ 图1.5

11微积分内容回顾 5 正如前言中提到的,在合适的情况会使用计算机代数系统Maple。.计算机代数系统对于符 号微分和绘图特别有用,在例1中对这两种技术给予说明。 例1对于区间[1,2]和[0.5,1]上的函数 f(x)=5cos 2x-2xsin 2x 找出maxf(x)小。 首先说明Maple的绘图能力。为了利用其绘图程序,键人命令 >with(plots); 随后程序内的命令就显示出来。定义∫键入 >f:=5*cos(2*x)-2*x*sin(2*x); Maple回应 f:=5cos(2x)-2xsin(2x) 为了绘出f在区间[0.5,2]上的图形,用命令 >p1ot(f,x=0.5.2): 图形如图1.6所示。为了确定图形上任意点的坐标,可以把鼠标指针移动到所需点并点击鼠标 左键。这个方法可以用于估计函数在坐标轴上的截距和极值。 06.0.81.0121.41.61.82.0 图1.6 下面用极值定理来完成这个例子。首先考虑区间[1,2]。为了得到一阶导数g=f,键入 >g:=diff(f,x) Maple给出 g:=-12sin(2x)-4xcos(2x) 可以用下面的命令对1≤x≤2求解g(x)=0: >fsolve(g,x,1.2); 得到1.358229874,然后用下面的命令计算f(1.358229874): >evalf(subs(x=1.358229874,f); 因为f(1)=-3.899329037和f(2)=-0.241008124,所以对区间[1,2]可以得到最大值 f八2)=-0.241008124,如图1.7所示,同时得到最小值约为f(1.358229874)=
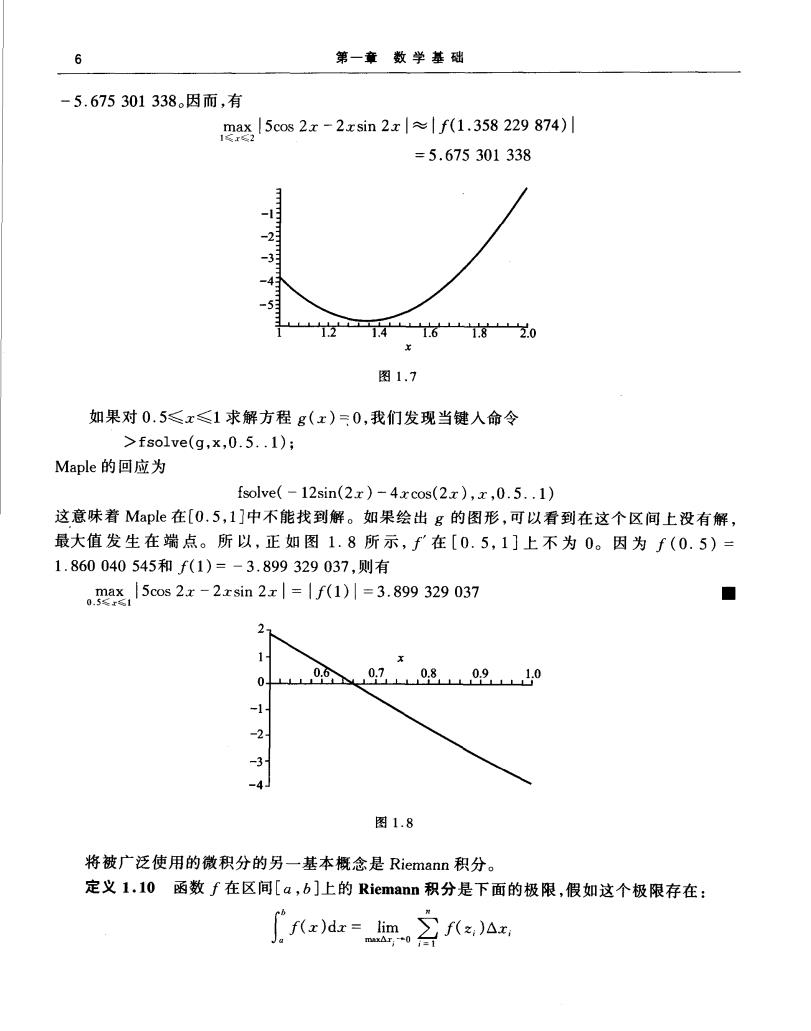
6 第一章数学基础 -5.675301338.因而,有 ma|5cos2x-2xsin2x|≈|f1.3582298741 =5.675301338 3 图1.7 如果对0.5≤x≤1求解方程g(x)=0,我们发现当键人命令 >fso1ve(g,x,0.5.1); Maple的回应为 fsolve(-12sin(2r)-4xcos(2x),x,0.5.1) 这意味着Maple在[0.5,l]中不能找到解。如果绘出g的图形,可以看到在这个区间上没有解, 最大值发生在端点。所以,正如图1.8所示,f在[0.5,1]上不为0。因为f(0.5)= 1.860040545和f(1)=-3.899329037,则有 ,0ax,15cos2x-2xsin2x|=1f1)1=3.899329037 ◆ 2 0 020809L0 2 3 -4 图1.8 将被广泛使用的微积分的另一基本概念是Riemann积分。 定义1.l0函数f在区间[a,b]上的Riemann积分是下面的极限,假如这个极限存在: fxdr=im,∑f(,)Ax
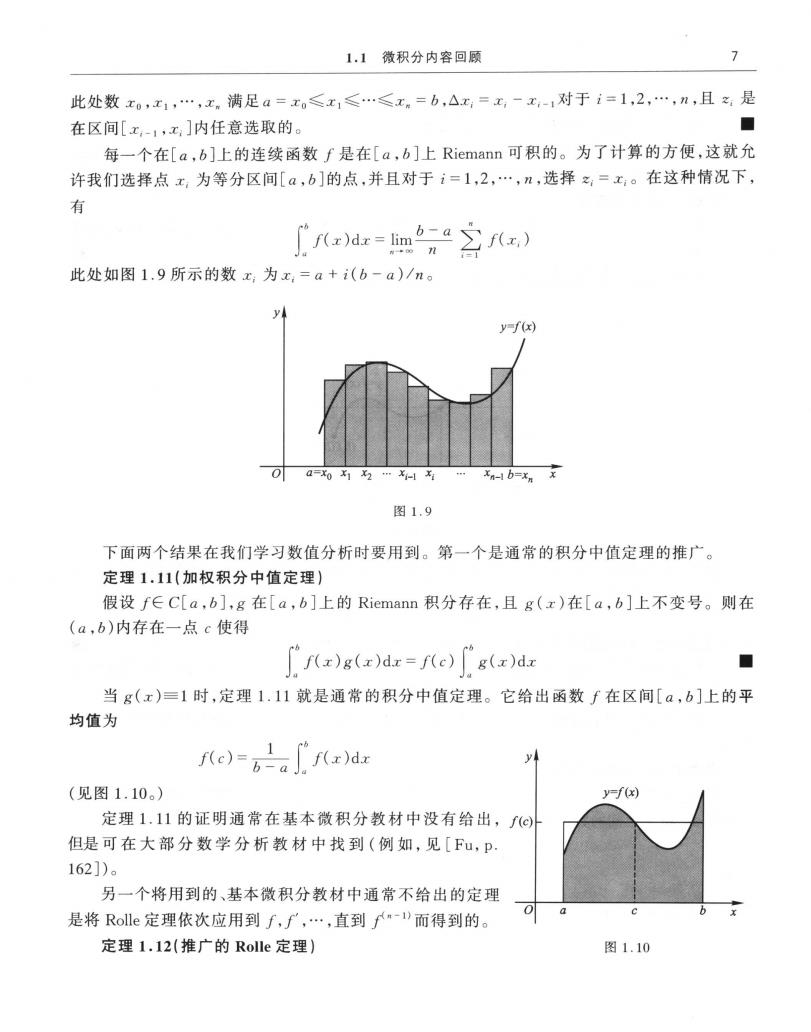
11微积分内容回厨 此处数x0,x1,.,x,满足a=x≤x1≤≤x.=b,△x,=x,-x-对于i=1,2,n,且之是 在区间[x,-1,x]内任意选取的。 ■ 每一个在[a,b]上的连续函数f是在[a,b]上Riemann可积的。为了计算的方便,这就允 许我们选择点x,为等分区间[a,b]的点,并且对于i=1,2,n,选择之=x。在这种情况下, 交 广fxa=m空rx) 此处如图1.9所示的数x,为x,=a+i(b-a)/n。 y=f(x) xn-b=x。 图1.9 下面两个结果在我们学习数值分析时要用到。第一个是通常的积分中值定理的推广。 定理1.11(加权积分中值定理】 假设f∈C[a,b],g在[a,b]上的Riemann积分存在,且g(x)在[a,b]上不变号。则在 (a,b)内存在一点c使得 ["f(x)g(z)dr=f(e)[g(r)dr ◆ 当g(x)=1时,定理1.11就是通常的积分中值定理。它给出函数f在区间[a,b]上的平 均值为 edr y (见图1.10。) f(x 定理1.11的证明通常在基本微积分教材中没有给出,fe 但是可在大部分数学分析教材中找到(例如,见[Fu,p 162])。 另一个将用到的、基本微积分教材中通常不给出的定理 是将Rolle定理依次应用到f,厂,.,直到"-”而得到的。 定理1.12(推广的Rolle定理】 图1.10