
引P,=ch(f扑Tn)且u=(1,…,l1)位于B中. (1)和(2)蕴含着BGo. 口 定54.设GCC是一个正常的Reinhardt域,f在G内 全纯。则存在一个在G内收敛的幂级数8(8)=∑,d满足f(8) =8(),&∈G. 证明:如果动∈G,则存在一个满足」9「<{细I,i1, ·,n的1∈G。所以∈P,对a∈P,令 chfT,)()∑,d, 系数a,是关于0的Taylor级数的系数,它们不依赖于1.由于 的是任意的,由此可知f关于0的Taylor级数在整个G中收敛. 它定义一个全纯函数g,g与↑在原点附近重合.由唯一性定理, 在G上1=G. 定义5.1.如果'GCC是一个正常的Reinhardt域,则G= UR称为G的完全包. .chce 腑注 1.G是开的. 2.GCG.如果和∈G,则存在,∈G∩C,使得和∈P,CG. 3.G是一个Reinhardt域.设0∈G,∈G∩C,前∈P, 则TcP,cG. 4.G是完全的.设0∈G∩C,1∈G∩C,和e户,则P.C P.CO. 5.由性质(1)到(4),G是最小的.设GCG1,G:是个完 全的Reinhardt域。如檗EGnCn,则P,CG.因此,GCG. G是包含G的最小的完全域,且有下述重要的定理 定量5.5,设G是一个正常的Reinhardt域,f在G内全纯, 则恰有一个在G中的全纯函数,满足FG=f. 证明: 由定理54,在中我们能写作 。24·
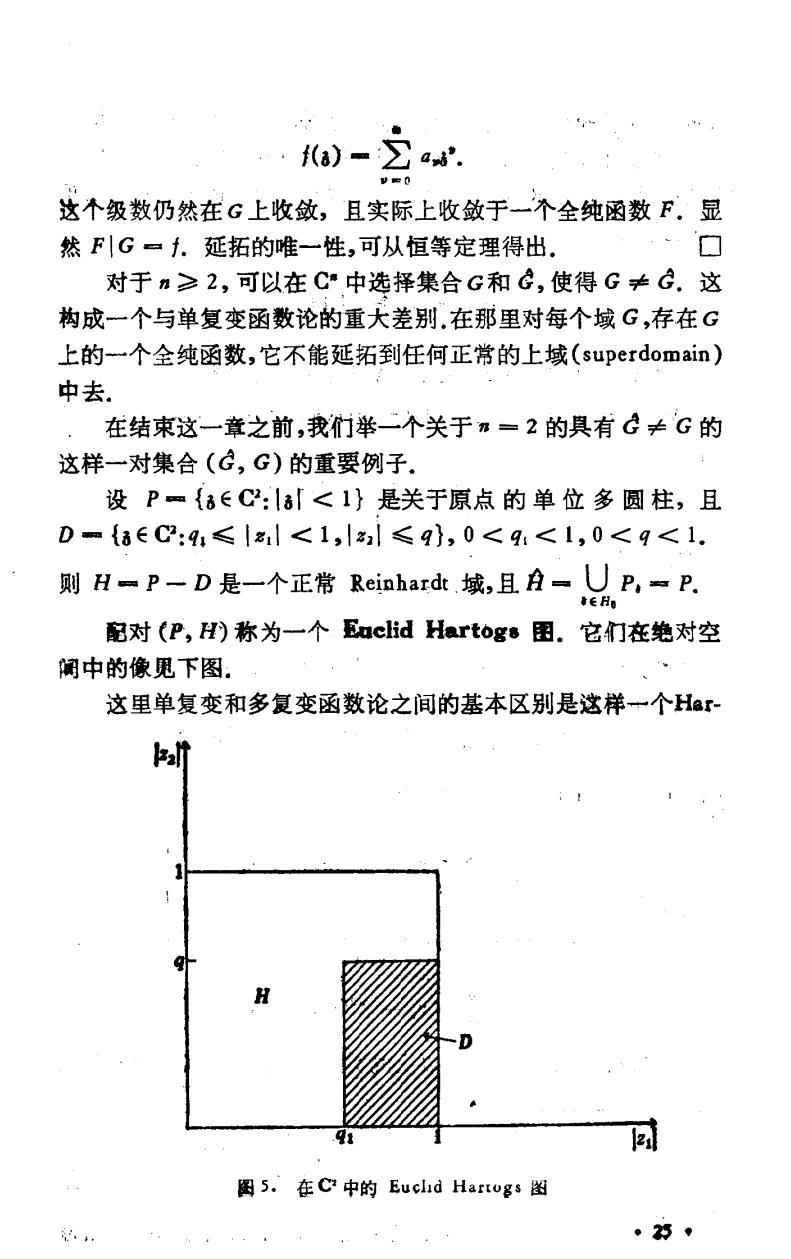
3)=∑ 这个级数仍然在G上收敛,且实际上收敛于一个全纯函数F。显 然F|G一f.延拓的唯一性,可从恒等定理得出。 口 对于m≥2,可以在C中选择集合G和G,使得G≠G.这 构成一个与单复变函数论的重大差别,在那里对每个域G,存在G 上的一个全纯函数,它不能延拓到任何正常的上域(superdomain) 中去 在结束这一章之前,我们举一个关于"一2的具有G≠G的 这样一对集合(G,G)的重要例子, 设Pm{8∈C:l「<1}是关于原点的单位多圆柱,且 D={a∈C:4,≤ll<1,lal≤q},0<9:<1,0<9<1. 则H=P一D是一个正常Reinhardt.域,且A=UP,=P. EHo 留对(P,H)称为一个Euclid Hartogs困.它们在绝对空 阅中的像见下图. 这里单复变和多复变函数论之间的基本区别是这样一个Har H 图5.在C中的Euchd Hartogs图 …

togs图在C中不存在.我们已经注意到,在C中Reinhardt域 是开圆盘和圆环,所以C.中的正常Reinhardt域是一个开圆盘, 即是,个完全的Reinhardt域。,因此C不是G的一个正常上集 合(超集)。 §6.实和复可微性 设MCC是一个集合,f是M上的一个复函数.在每一点 动∈M有一个唯一的表示()=Re()十Imf(o).所以能够 由 g(E,9)=Re f(8), (,)Im f(8) 定义M上的实函数g和h,其中=:+西,因而我们写作: t=g+h。 定义61.设BCC是一个区域,f=g十边是B上的一个 复函数,和是B的一个点。十称为在实可徽的,如果g和本金 是(实)可微的. 实可微性意味着什么?如果g和h都是可微的,则 g(,9)=g(0,)+∑(x,-)(,) +∑(.-9)a(,, (1) (怎,)-(,%)+∑(x,-m)(g) +∑(y,-)脖*(s,); 其中c,*,脖,胖率都是B上的实函数,它们在(0,如)连续而 且 c(0,90)=gx,(的,%), c**(o3%)agy,(,%), ”26·

.(,o)h(o,0), 辣*(o,0)=hy,(o,6). 综合这些方程有: (2)3)-)+会(,-9△(6) +∑(y,-)△*), 这里△=十暗,△*一a率+设*在动连续,且其中 △()=g,()十h,()-f(), △*().=g,()+ih,()=f,(y 定理61.设BCC是一个区域,和∈B是一个点,f是B上 一个复函数.则f在和是实可微的,当且仅当存在B上的函数 △,△',它们在和连续,且在B中满足下述方程: (3f6)-)+∑(,-zm)Aa) 会(属,-)A】. 证明: 1.设f在0实可微,利用方程 ,一0=1【(,一)+(盆,一)] 2 和 %9-2-9)-(点,-01,° 则有 f(a)-)+∑(,-24)△(a)-△( 张2 +(属-测)》+*. 2 茹果我们定义 ◆27●

么一一和白+, 刘(3)式成立. 2.设1)-)+会(一9A(a) +2.-0)A, A,A在连续.。方程A一(△下*)/2,A”=(△等+ △**)12以矩阵形式表示成 ()-( -() 则dtA一2i中0.,这表示方程关于a事和,4**可解.:这个解函 数满足(2);(1)可从分解(2)成实部和虚部得出。因为函数, **,摩,*在点加是唯一确定的,所以对于函数△,△'来说同 样也是成立的。 现在我们记: f)-()-,()=弟1. ,()-A(-2[f,(z)+i,w)1. 定理6.2、设BCC是一个区域,EB,f是B上一个复函 数.则十在加是复可微的,当且仅当f在o是实可微的且f,(的) -0,1≤v≤n.(这意味着Cauchy-Riemann微分方程组必须 满足:·。 gr,hy,hsw=-gy,)1≤y≤n.) 证明: 1.设fa)=()+∑(,-9)a(,A()在连鳞 28