
对于n=2,已经有一个反例。设G=C,M■{(1,z2)∈ G:82=0},f(a1,2)=2·g(31,),f(1,22)=z2·h(z1,22), 其中8和h在整个C上全纯.则fM=M,但对于g≠h, ≠f2、 定理4.1(全纯函数的恒等定理)设GCC”是一个域,且在 G中i,f全纯.设BCG是一个非空区域,适合f|B=B.则 G=G. 证明:设B0是集合{∈G:(8)=()}的内部,且Wo= G一Bo.因为BCBo,所以B0≠少.由于G是连通的,所以只 要证明W。是开的,由此立知B,一G.让我们假设W,包含一个 点,它不是一个内点。则对于每个关于和的具有严二G的多圆 柱P,P门B0≠必.·设r∈R,且P={:{;一z引<r}m{a: dist'(a,动)<r}是这样一个多圆柱.令 P'={8:dist'(8,80)<r/2}CP, 则也有P'∩B≠中.选择一个任意点1∈P∩B。且置P*={: dist'(,1)<r/2}.显然∈P*而P*CP(三角不等式).因此, P*CPCG.设 a)-之,(6-)和抓)-∑6,(8- 是:和,在P*中的Taylor级数展开式.因为在1∈B,的邻域 内,=f2,所以对所有"有4,=b,(系数由函数唯一确定,参 考定理3.8).因此P*=IP*且P*CBo.由此得和∈Bo,矛 盾 口 定理4.2。(幂级数的恒等定理)设GCC"是一个域,0EG, 且∑a,d”,∑6d是两个在G中收敛的幂级数。如果存在一个 8>0,使得在U.(0)cG中∑,8-∑6,,则对全部, ·19●
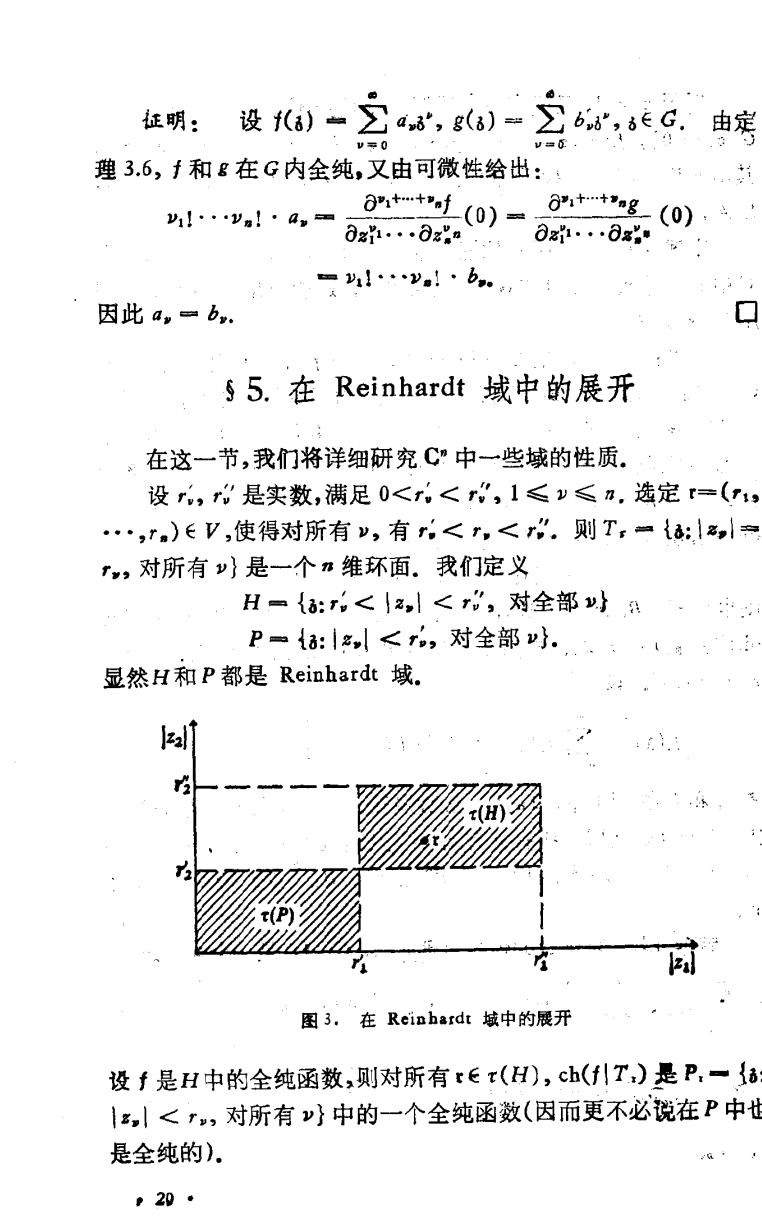
证明: 设a-立,6)26eG.由定 理3.6,f和g在G内全纯,又由可微性给出: y1l···ya!·awa 0tt"f(0)= 6+tg(0)): 0z州…8z"n ∂z州1.…8g- 因此a,=b. §5.在Reinhardt域中的展开 在这一节,我们将详细研究C”中一些域的性质。 设r,r是实数,满足0<r<r',1≤y≤n.选定r=(r, ·,r.)EV,使得对所有v,有r<r,<r”.则T:=1a:产 r,对所有}是一个n维环面.我们定义 H={:g<|z,l<,对全部} P={a:,<,对全部}. 显然H和P都是Reinhardt域. 图3.在Reinhardt城中的展开 设f是H中的全纯函数,则对所有r∈x(H),ch(fT)是P,一{ 1名,<r,对所有}中的一个全纯函数(因而更不必锐在P中世 是全纯的) p20·

命慧. g:pXr(H)→C,其中g(a,)=ch(f引Tr)(a),与 t无关。 证明: 我们有 d)-(a.5 对每个i,1≤i≤n,我们有|<r1■5,因此≠5,因而 被积函数在圆环{名:<1<}上全纯,并且从一个变量的 Cauchy积分公式可知,如果r一(r,…,r,)∈x(H)且r*(r, …,r)Ex(H),则 [1 g2线--g二2 i51=15;一1 这就得出命题, 口 定理5.1.,设GCC是一个域,且E={=(1,·,8)∈C, 其中z,=0},则集合G=G一E也是C中的一个域 证明: 1.E是闭的,所以C一E是开的,因而G一G∩(C一E) 也是开的.此外,E不包含内点 2.我们把点∈C写作形式=(1,),其中a*EC.现 在令0=(z,6*)∈G,且设U()U,(9)×U(*)是0 的一个e邻域.我们证明U;一E还是连通的设1=(”,w) 和2一(,*2)是U:一E中的任意两点.然后定义的=(✉, 80).显然翻EU一E.U()是平面上的一个开圆盘,且 U()一{0}仍然连通.因此,存在一个路径甲连接0和”, 且整个路径位于U.(,)一{0}内;自然,也存在一个路径中连接 a*w和*2,且它位于U(南@)内. 现在我们由w():((),四)和w,(e)=(z,()定义 路径w1,w2.则w1连接1和3,w,连接和,且它们的合成在 一E中连接1和血。因此U一E是连通的。 ·21·

、 ·图4.定理5.1的证明 3.令,”EG一E,且设P是G内任意一个连结和”的 路径.由于p(1)是紧的,所以它能够由有限多个适合UCG(1= 1,·,)的多圆柱U0,U所覆盖。 引理.存在一个6>0,使得对所有适合|一1.<8的 t劣,:p?和p()位于相同的多圆柱U中.“ 证明:…设有适合」一1→0的序列(),()€1,使得 p(),p()不位于相同的多圆柱Uk中.存在(),()的收敛 子庄列,(,,(所o=m.-in:如果(o)eU, 则存在一个满足p(V)cUk的开邻域VV(o)C1.则对几乎 鉴部eN,有,e和,∈V,因此仰(4,)EUk,且p(,)∈ 刀《:这是个矛盾,它证明了这个引理。·· 、现在让6适当选取,且0由0<<·<k幽1是I的一 个划分满起1片t<6,i=1,…,.设=p(),且V,是 包含为-的多圆柱(可能对方≠,有V一V,).由构造- 位于V;门V神,所以V;∩V;-i总是一个非空开集。实际上, 的;E≠功,i=1,…,:我们用在V1一E内部的一 条路径P1,连结=0∈V1一E和点*∈V∩V2〦E.由(2), 这基可能的其次,我们用在V一E内部的一条路径P连结 和点在个V,÷E,如此继续· 最后,设Pk是+E内的一条路径,它连结和一” ·224

V一E.路径单P的合成在G一B中就连结和”.口 定理5.2。设G是C”中的一个域,E一{8.=(,…*.) C:至少有一个”,使=0}。则Cg=G二F也是一个域 证明:对每个4,1≤4≤n,Gm=G一Eu是连通的,这里 E={(,…,)EC”:z和=0.还可定理1,通过简单 的坐标置换得到。 ·显然,6一UE;因此G台(G一E)E,):)E, 由普通的归纳证明可得出这一命题。 定理5.3.设GCC是个正常Reinhardt域,f在G上全 纯,r∈GnG.则ch(f川T)在原点的个邻域与f重合. 证明:我们有G=x(GnC)c{x∈V:r;≠0,i.=1,, n. 1.G0是一个域: :a.GnC是一个Reinh4rdt域,因此,由定理2。.G0= r(GnC)是开的. b.如果r1,2是Go中的点,则存在点pGC满定xGap) p,=1,2,.如上所述,GC是域,所以在G∩C电疾在一 条路径P,它连结1和.则toP是G0中的一条路径,它连结 和,· ,2.令. 发 B={r∈G:ch(|T)在0的邻近和f重合.·,: .B是开的:如果o∈BCG2:则有一个邻域U(o)二 G,它能够被写成x(H).这可以从本节初我们选择集合t(H)的 方法得到.设P=P(0)是相应的多圆柱,则对a:∈p和tEU(o), 有ch(f1T,(8)=ch(f1T,)(8).此外默)=ch(川T,)(3)是 上的一个全纯函数由于t∈B,它与f在原点附近重合因此, ()CB. b.w一G0一B是开的:.证明类似于a。: c.B≠:有一个关于0的多圆挂P,香合币二G.则 :经: