
第一章 平面问题 §1一1直角坐标下按位移求解的控制方程 当取用直角坐标系x时,求解弹性力学问题的基本方程为 平衡方程 密+旁+X0,旁+密+Y=0 (1.1) ay ar 几何方程 6=器6=多如=密+旁 (1.2) 物理方程 对于平面应力问题: 5-意a.-g,6w2%,-o,=21吉0, (1.3) 或 =+e,、=+、o=2a年14 E E 对于平面应变同题则须将式1.3)和1.)中之E澳为山换为1己。 首先讨论平面应力问题的控制方程。 将式(1.2)代入式(1.4)中,再将式(1.4)代入式(1.1),有 (整+器+告离》+x0 2ax动y (1.5) 要+1要+生*+-0 式(1.5)耶为传统的弹性:学平面应力间题求解位移分盘4和v的控制方程。 引入体积应变函数对平面应力问题 6=6+6+=二兴,中)-二2+ (1.6) 利用式(1.6),式(1.5)可以写成 a品器-票+号装+x=0 (1.7) 20年经+器+品》-r-0 如果将式(1.7)中之e也视为独立的未知函数,u、v及e三个函数须由式(1.6)及 (1.7)的三个方程确定。为了我们的目的,利用式(1.6及(1.7)之关系推导另一个求解e的 方程。 分别对式(1.?)第一式及第二式分别关于x和y求一次导数,然后相加,并利用式 1

(1.6),可得 a+品-整++器+器-0 (1.8) 式(1.8)就是我们所需要的求解e的方程。从而有求解u、v及e的如下控制方程组: Vie= +”4-(警+) E yu=-12证 1+”-21+"2x (1.9) w-甘品器-2吉y 式中 =是+易 控制方程(1.9)的优点是非耦联的。先由第一式求解e,(其中X和Y是已知函数),然后 将求解得的e分别代入第二式第三式中求解4和,这样,所求解的均为独立的二阶偏微分 方程, 进而采用如下无因次量: (z,)=(xy》,(a,)=129(uw)} a (a,)=且+是-20(a,n) vE (1.10) (8,)=1+1-2w(x,Y) DE 式中a为特征长度,取作参考值。于是,我们有确定无因次量函数m、⑦及:的如下无因次控制 方程: 7=-竖+ 7z=一1十v速 -2x (1.11) 7行--1+" -27 穷 式中 e与、五间的关系为 -之器+》 (1.12) 利用式(1.10)之无因次盘及关系式(1.12),由式(1.2)及(1.4)可得如下无因次应力一 位移关系: 可,=+爱马,=+需w-需+) (1.13) 式(1.11)一(1.13)即为以下求解平面应力问题时所使用的控制方程和关系式。 用同样的方法可得到如下平面应变问题的芝制方程:

7e=- 爱+ a取 7五=一 -2X (1.14) U委 7师=一1重 v万 -2? 在此情形下,e与立、五间的关系为 =“鑒+》 (1.15) 而应力一位移关系仍与式(1.13)相同,大是其中e应按式(1.15)计算. 下面利用有关控制方程和关系式求解若干在何题,并闻明求解方法的原理和步骤。 §1一2两端固定深梁的应力分析 知图1.1(a)所示两端固定深梁,夸长2a,梁高2b:梁单位体积重为Y;梁的上边界受竖向 分布荷载q(x);粱的受力属平面应力问题。 取用如图所示直角坐标系x。不失-一股性,设荷载q(x)关于y轴对称,即q(x)=q(一 x), (r) a】 图1.1 取用半跨长a为参考长度,在式(1.10)无因次壁的情况下,并将荷载q(x)转化为无因次 孟定)=宁-2必g(e),则图1.1(a成为图1.1(6),图中A=/a. vE 注意到体积力为梁的自重,则8=0,?=-7=1+)一2)y),控制方程(1.12) 成为 7=0,7a=-1÷爱,7元=-1等+27 (1.16) 为了简化计算,将图1.1(b)所示之荷载分解为如图1.2(a)和(b)所示关于轴云对称和反 对称两种滑形。 由图1.2有如下边界条件: 对称荷载情形[图1.2(a)] 王=士1,8=0、0=0 (1.17) y=士A,6,=-i(x),=0j 注意到式(1.:,条件(1.17)可写成
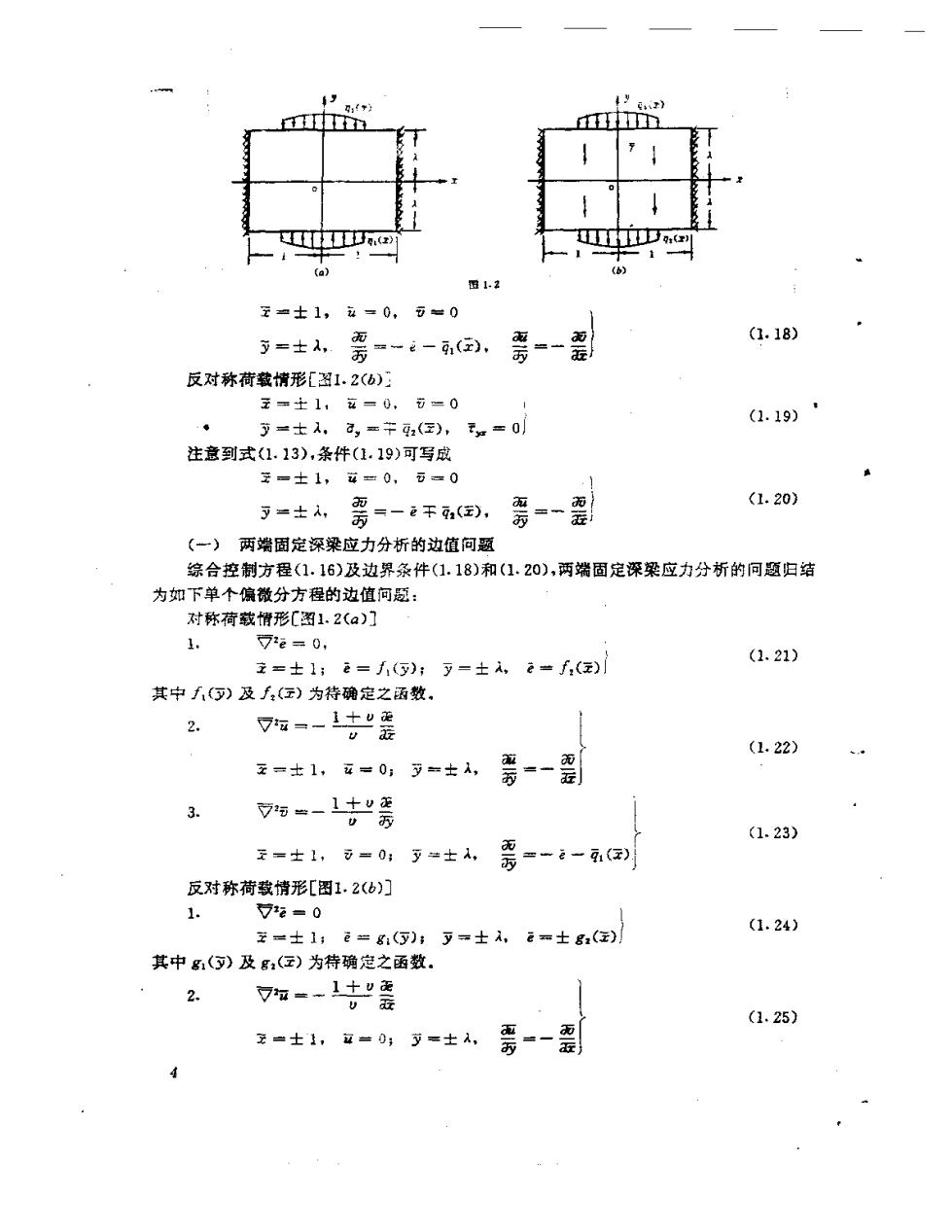
49 D (a) (6) 图1.2 -士1,a=0,五=0 =士需=--到, (1.18) 反对称荷载情形[图1.2(): 元=土1,元=0,节=0 节=士1,a,=干,(),如=0 (1.19)· 注意到式(1.13),条件(1.19)可写成 受=土1,0,石=0 了士A,需=-8干(动, 而 而 而 (1.20》 (一)两端固定深梁应力分析的边值问题 综合控制方程(1.16)及边界条件(1.18)和(1.20),两端固定深梁应力分析的问题归结 为如下单个偏微分方程的边值问题: 对称荷载情形[图1.2(a)] 1, 72e=0, (1.21) 主=±1;e=();y=土A,e=f,() 其中f()及f(云)为待确定之函数, 2. 7m=一1十"使 ”—妥 (1.22) 元=士1,a=0,3=士A, 3. 7元一-1十v速 污 (1.23) 天=士1,元=0:y法士1, 的 =一“4() 反对称荷载情形[图1.2(b)] 1. 7e=0 (1.24) 主=土1;e=g1(灯);y=士,e=士g,() 其中g1()及g()为待确定之函数. 2- 7z=-1土”更 u委 (1.25) 交=士1,=0;寸=士入, 证

3. =-1+需-27 (1.26) =士1,=0习=士,需-千)】 (二)对称荷我情形下的解答 1.求解 将式(1.21)中之待确定函数f()和f,()表示为如下级数形式: fig)=Aeo5、f国)=2 B.cosa.F (1.27) 式中A,和B,为待定系数,a=(-0.5)r,c,=(i一0.5)x/2 于是,由式(1.21)有 整+琴=0 元=士1,=】 ea, 5=±d,= 豆awa (1.28) 不难验证,边值问题(1.28)之解为 i- cha2cosa迈+B,cosTha.] cha (1.29) chaA 2.求解云 将式(1.29)代入式(1.22)中,有 bs5-B,气sina7ha cha chaA (1.30) 乏=士1,z=0: 可=士, 需-爱 用有限积分变换法求解边值问题(1.30),并取用如下积分变换式: 正变换: (a,)=t'a(G,5sin日,zd2 (1.31) 逆变换: (往,)= *(9,sinp年 式中 月,=次 以sin月:王乘式(1.30)之两端,并从一1到+1对云进行积分,有 器-=-1245-8 ”.- cha chaiA (1.32) )=士A, 需-一要nz近 式中E对='sha'inf,zd左=-2eo且 Fsinain tintin j- a3.+ 一月与 高+月 注意到”为y之偶函数,式(1.32)第一式之解为