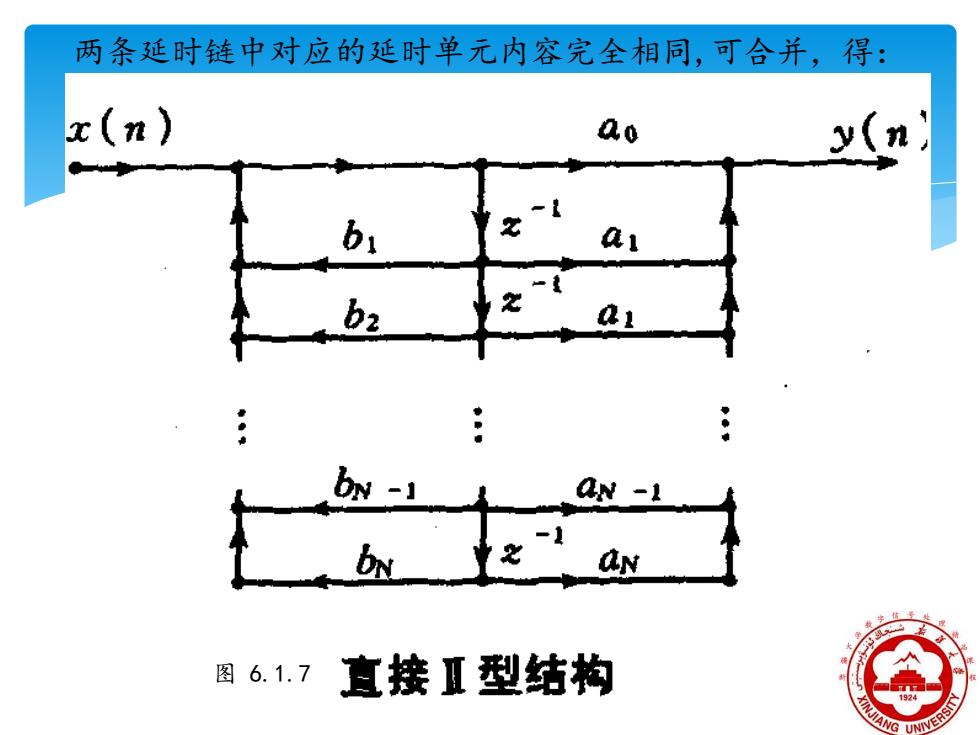
两条延时链中对应的延时单元内容完全相同,可合并,得: x(n) ao y(n z1 图6.1.7 直接Ⅱ型结构
两条延时链中对应的延时单元内容完全相同,可合并,得: 图 6.1.7

直接I川型优缺,点: 优,点:延迟线减少一半,为N个,可节省 寄存器或存储单元。 缺点:同直接型。 通常在实际中很少采用上述两种结构实 现高阶系统,而是把高阶变成一系列不同组合的 低阶系统(一、二阶)来实现
直接II型优缺点: 优点:延迟线减少一半,为N个,可节省 寄存器或存储单元。 缺点:同直接型。 通常在实际中很少采用上述两种结构实 现高阶系统,而是把高阶变成一系列不同组合的 低阶系统(一、二阶)来实现

(c)级联型(串联) 一个N阶系统函数可用它的零、极点表示,即 把它的分子、分母都表达为因子形式 H(z)= 1- ∑bz Π(1-dz) 由于系数a、b都是实数,极、零点为实根或共 轭复根,所以有 M 0-8,z'1-4z0-z1) H(z)=A间 i=l Π4-p,z0-9,z1-9iz) i= i=
(c)级联型(串联) 一个 N 阶系统函数可用它的零、极点表示,即 把它的分子、分母都表达为因子形式 由于系数 、 都是实数,极、零点为实根或共 轭复根,所以有 i a i b

8、P 实根 h、q 一复根 N +2N2=N 且 M,+2M,=N 将共轭因子合并为实系数二阶因子,单实根因子看作 二阶因子的一个特例,则 H(z)=AΠ 1+a21+a2z2 i=] 1-bz1-b,z9 M =A∏H,(z) i=l a、b 一为实系数。 用若干二阶网络级联构成滤波器,二阶子网络称为二阶节 ,可用正准型结构实现
、 ——实根 、 ——复根 且 将共轭因子合并为实系数二阶因子,单实根因子看作 二阶因子的一个特例,则 、 ——为实系数。 用若干二阶网络级联构成滤波器,二阶子网络称为二阶节 ,可用正准型结构实现

x(n)A y(n) b11 b2 之1a21 Z-QMM H( 61.8级联型结构 图 H()
( ) 1 H z H (z) M 图 6.1.8